Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx

1.Свет. Интерференция света. Условие максимума и минимума интерференции.В конце XIX века английский физик Дж.К.Максвелл на основе своих уравнений создал единую электромагнитную тео­рию световых волн, согласно которой, свет – это множество электромагнитных волн. Электромагнитная волна – это распростра­няющееся в пространстве электромагнитное поле, которое ха­рактеризуется векторами напряженностей Е и Н электрического и магнитного полей. Согласно теории Максвелла, вектора Е и Н перпендику­лярны друг другу и направ­лению распро­странения волны, откуда следует, что электромагнит­ные волны по­перечны.

Интерференция световых волн.

Если монохроматические световые волны имеют посто­янную во времени разность фаз и колебания их световых векто­ров происходят в одной плоскости, то они называются коге­рентными(от греч. cohereus - согласованный). Такие согласо­ванные когерентные волны при наложении их друг на друга мо­гут создать в пространстве картину, заключающуюся в чередо­вании светлых и темных областей. Данное явление перераспре­деления интенсивности световой волны в пространстве при на­ложении двух или нескольких когерентных волн называется ин­терференцией света.Если в произвольной точке пространства оптическая разность хода накладываемых волн равна нечетному числу полуволн, то в ней наблюдается минимум интерференции. Условие 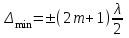есть условие интерференционного минимума.Если в произвольной точке пространства оптическая раз­ность хода накладываемых волн равна четному числу полуволн или целому числу длин волн, то в ней наблюдается максимум интерференции и условие 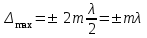является усло­вием интерференционного максимума2.Метод расчета интерефекационной картины от 2х. источников.Метод Юнга. Получение интерференционной картиныВ 1803г. английский физик Т.Юнг с помощью двух ще­лей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко ос­вещенная щель S, от которой световая волна падала на две узкие равноудаленные щели S

---

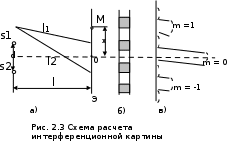
₁ и S₂, параллельные S (рис. 2.2). Щели S₁ и S₂ можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные ис­точники, свет от которых распространяется во всех направле­ниях. Волны, идущие от S₁ и S₂, накладываясь друг на друга, ин­терферируют. Интерференционная картина наблюдается на эк­ране Э (рис. 2.2).Обозначим расстояние между щелями S₁ и S₂ равным d, а между щелями и экраном - l, причем l » d(рис. 2.3 а). Точка О – центр экрана, она расположена симметрично относительно ще­лей S₁ и S₂. Результат интерференции волн в произвольной точке экрана М, находящейся на расстоянии х от его центра О, должен определяться разностью хода Δ = l₂- l₁. Математический расчет дает для разности хода Δ = хd/l. В тех местах экрана, ко­торые удовлетворяют условию , образуется интерференционный максимум. Отсюда 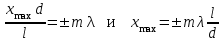.В тех местах экрана, где , волны “га­сят” друг друга и образуется интерференционный минимум. От­сюда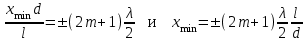 .Шириной интерференционной полосы Δх называется рас­стояние между соседними максимумами или минимумами 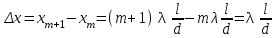.Величина Δх постоянна при заданных d, l и λ и не зависит от порядка интерференции m. Таким образом, при освещении щелей монохроматическим светом на экране наблюдается чере­дование светлых и темных полос одинаковой ширины (рис. 2.3 б). Чтобы полосы были хорошо различимы, Δх должна быть по­рядка 5 мм, тогда при λ = 500 нм отношение l/d равно 10000, т.е. выполняется условие l » d.При освещении щелей белым светом интерференционные максимумы становятся радужными. Это происходит из-за того, что положение интерференционного максимума зависит от длины волны падающего света, а белый свет содержит в себе все цвета спектра. Максимумы коротких длин волн (фиолетовых) будут располагаться ближе к центру экрана, за ними следуют максимумы синих длин волн и т.д. до самых длинных красных (рис. 2.3 в). В середине экрана при

---

m = 0 максимумы всех волн совпадут из-за отсутствия разности хода и получится белая по­лоса.В настоящее время высокая степень когерентности свето­вых лучей достигается с помощью лазеров.

---

3. Интерференция света в тонких пленках или полосы ровного наклона.

В природе мы неоднократно наблюдали радужную окра­ску мыльных пузырей, тонких пленок нефти и масла на поверх­ности воды и оксидных пленок на поверхности металлов. Эти явления обусловлены интерференцией света в тонких пленках, возникающей при наложении когерентных световых волн, отра­женных от верхней и нижней поверхностей пленки.П 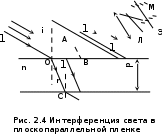усть на плоскопараллельную прозрачную пластину с показателем преломления n и толщиной d под углом i падает плоская монохроматическая волна (рис. 2.4). Рассмотрим луч 1, который, коснувшись поверхности в точке О, разделится на два когерентных луча: отраженный от верхней поверхности пленки 1’ и преломленный 1’’. Луч 1’’ пройдет пленку, частично отра­зится от нижней ее поверхности в точке С, дойдет до точки В и, преломившись, выйдет из пленки. Проведем прямую АВ, перпендику­лярную лучам 1’ и 1’’. Путь, который оба луча пройдут от этой прямой до экрана, будет оди­наковым, но от точки О до АВ путь, пройденный лучами, будет раз­личным. Найдем эту разность хода лучей Δ. С учетом показателя преломления пластинки n: Δ = =(OC+CB)·n–OA, или, как дает математический расчет, 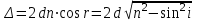. Известно, что в процессе отражения от оптически более плотной среды, световой луч теряет поло­вину длины волны λ/2. Если пластинка находится в воздухе, то λ/2 теряет луч 1’ в точке О и выражение для разности хода при­обретает вид: 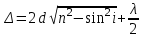.Если на пути лучей поставить собирающую линзу, а в ее фокальной плоскости – экран, то лучи 1’ и 1’’соберутся в точке М. Освещенность точки экрана будет максимальной, если раз­ность хода Δ составит целое число длин волн и минимальной, если Δ составит нечетное число полуволн.Разберем несколько различных вариантов интерференции света в тонких пленках.4.Полосы равной толщины или кольца Ньютона.Полосы равной толщины

---

. Пусть на клиновидную пластинку малого угла наклона α (d≠ const) с показателем пре­ломления n падает плоская монохроматическая волна (рис. 2.6). Из множества падающих на клин лучей рассмотрим лучи 1 и 2. Отраженный луч 1’ и луч 1’’ (и, соответственно лучи 2’ и 2’’) пересекутся вблизи поверхности клина и проинтерферируют.М ысленно проведем через точки пересечения В₁ и В₂ плоскость, параллельно ей разместим собирающую линзу и за линзой сопря­женно с плоско­стью В₁ В₂ уста­новим экран Э (рис. 2.6). Чтобы определить на экране точку М₁, в которой собе­рутся лучи 1’ и 1’’, надо через точку В₁ и центр линзы О про­вести побочную оптическую ось до пересечения с экраном. Анало­гично построим на экране точку М₂. Разности хода лучей 1’ и 1’’, 2’ и 2’’ будут отличаться из-за разных толщин клина d₁ и d₂. Следовательно, геометрическое место точек клина, соответствующих какой-то одинаковой толщине dопределит одинаковую разность хода для всех лучей, падающих на это место. Для этих лучей на экране выполняется одинаковое условие интерференции. Таким местом в клине является полоса, например, А₁А₂ (рис. 2.7) и на экране картина имеет вид светлых и темных полос, которые называ­ются полосами равной толщины. В рассмотренном случае по­лосы равной толщины локализованы близко над поверхностью пластинки. Мы можем увидеть их и не в лабораторных усло­виях, так как роль линзы в данном случае играет хрусталик, а роль экрана - сетчатка нашего глаза. Если свет падает на клиновидную пластинку нормально (луч 1’’ перпендикулярен нижней поверхности пластины), то полосы равной толщины локализованы на верхней поверхности к лина. При освещении клина снизу, т.е. при наблюдении ин­терференции в проходящем свете, светлые и темные по­лосы на экране поменяются местами. Это происходит из-за того, что в данном случае нет потери полуволны. Ши­рина полос будет тем больше, чем меньше угол наклона α у клина. Если на клин падает белый свет, то интерференционные макси­мумы будут всех цветов спектра (как, например, радужная окраска мыльных пузырей).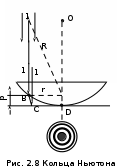Частным случаем полос равной толщины являются кольца Ньютона

---