Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 215
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Интерференция света в тонких пленках или полосы ровного наклона.
6.Дифракция Френеля на круглом отверстии и диске.
7.Дифракция Фраунгофера на прямоугольной щели.
8. Дисперсия и разрешающая сила спектрального прибора.
Оптическая активность веществ. @
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера.
4. 3. Поляризация света при двойном лучепреломлении.
6. 1. Характеристики теплового излучения. @
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
28. Состав ядра. Характеристики ядра. Размеры ядер.
происходят также при измерении скорости, энергии, времени.
Соотношения неопределенностей позволяют определить границы применимости понятий и законов классической механики к объектам, т.е. возможности одновременного использования понятий координаты и скорости при описании движения. Учитывая, что рх = mvx, можно получить Δх Δvх ≥ h/m, откуда следует, что чем больше масса частицы, тем меньше неопределенность ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для пояснения рассмотрим два примера.
1. Рассмотрим пылинку массой m=10-12 кг и линейными размерами 10-6м и определим для нее неопределенность скорости (неопределенность определения ее координаты примерно равна сотой доли ее размера т.е. Δх = 10-8м). Согласно соотношениям неопределенностей Δvх = h/mΔx = 6,62∙10-34/(10-12∙10-8) = 6,62∙10-14м/с. В результате получается неопределенность измерения скорости, намного меньшая скорости, с которой пылинка может двигаться. Поэтому, в данном случае, скорость и импульс можно определить практически точно и поэтому для пылинки можно использовать понятие траектории и законы классической механики.
2. Рассмотрим электрон, движущийся в атоме водорода. Неопределенность его координаты порядка размера самого атома, т.е. Δx = 10-10м.
Определим Δvх: Δvх = h/mΔx = 6,62∙10-34/(9, 1∙10-31∙10-10) = 7,3∙106м/с. Если рассчитать скорость электрона в атоме согласно классической механики, учитывая, что роль центростремительной силы играет сила Кулона, то скорость получается порядка 2∙106м/с и в данном случае неопределенность измерения скорости оказывается больше самой скорости. Поэтому нельзя говорить о движении электрона в атоме по определенной траектории.
21. Волновая функция. Уравнение Шредингера. Пояснение к нему.
Объяснить одновременное наличие корпускулярных и волновых свойств у микрочастиц удалось на основе идей Бора и Луи-де-Бройля в рамках новой теории, называемой волновой или квантовой механикой, созданной Гейзенбергом, Шредингером, Борном и многими другими учеными начала ХХ века. Квантовая механика базируется, как и любая другая физическая теория, на ряде постулатов. Основные постулаты можно представить упрощенно в следующем виде.
1.Движение микрочастиц в пространстве имеет вероятностный (стохастический) характер. Это относится не только к совокупности (ансамблю) частиц, но и к каждой отдельной частице. Согласно этому постулату, микрочастица, находясь в силовых полях или в вакууме (при отсутствии полей), испытывает такое воздействие, что нельзя в любой момент времени определить точно параметры ее движения. Например, нельзя одновременно характеризовать ее траекторию точными значениями координат и скорости или точными значениями энергии и времени какого-либо процесса у частицы.
2.Стохастический характер движения микрочастиц требует применения понятий математики теории вероятности для описания и расчета определенных значений параметров частиц в эксперименте. С точки зрения математики, отсюда следует, что движение таких частиц должно описываться с помощью некоторой «особой» волновой функции, которая должна характеризовать вероятностные особенности микрочастиц. Интерпретацию волновой функции дал в 1926г. немецкий физик Макс Борн следующим образом - волновая функция ψ (х, у, z) характеризует вероятность нахождения частицы в данный момент времени в некоторой точке пространства. Согласно Борну, физический смысл имеет не сама функция, а квадрат модуля волновой функции ψ2, который равен вероятности dP того, что частица будет обнаружена в пределах рассматриваемого малого объема dV.
Формула связи этих понятий имеет вид
dP = ψ2 dV = ψ
2dxdydz . (1.8)
Для совокупности частиц под вероятностью понимают отношение числа частиц в малом объеме к общему числу частиц, а для одной частицы – отношение времени пребывания частицы в малом объеме к общему времени рассмотрения движения частицы.
3.Волновая функция является основной характеристикой состояния микрообъекта, с помощью волновой функции можно рассчитать вероятность пребывания частицы в различных точках пространства в различные моменты времени, а также средние значения различных ее параметров. Соответственно вероятностному смыслу волновой функции и используя формулы теории вероятности, средние значения параметров находятся путем усреднения соответствующих операторов с помощью волновой функции. Например среднее значение для модуля радиуса-вектора частицы можно найти по формуле
Так как в физических экспериментах определяются именно средние значения параметров частицы, то можно говорить, что состояние частицы полностью задается ее волновой функцией.
4.Вид волновой функции зависит от типа частицы и от внешних силовых полей, действующих на частицу. Вид функции находится с помощью специального дифференциального уравнения, называемого уравнением Шредингера.
5.Если в эксперименте наблюдается суперпозиция (объединение) микрочастиц, описываемых разными волновыми функциями, то объединенный ансамбль этих частиц будет описываться суммой их волновых функций. Например, если при интерференции микрочастиц на двух щелях, их можно по отдельности описать двумя функциями ψ1 и ψ2, тогда совокупность этих частиц в районе экрана должна описываться функцией ψ = ψ1+ψ2. Так как вероятность распределения частиц на экране dP определяется квадратом модуля волновой функции, то получаем dP ψ2 = ψ12 + 2ψ1ψ2 + ψ22. Отсюда следует, что распределение зависит не только от простого сложения вероятностей двух независимых ансамблей ψ12 + ψ22, но и от результата их специфичного квантового «взаимодействия» 2ψ1ψ2, вследствие чего и наблюдается интерференция частиц.
Имеется еще ряд постулатов, но они имеют более частный характер, о некоторых из них будет сказано далее.
Для расчета волновой функции необходимо иметь уравнение, которое позволяло бы для любого момента времени определить эту функцию с учетом действующих на частицу внешних силовых полей. Чтобы искомое уравнение учитывало волновые свойства микрочастиц, необходимо чтобы оно по форме было волновым уравнением, подобно тем, которые описывают звуковые или электромагнитные волны. Известно, что для плоской волны, распространяющейся вдоль оси х, волновое уравнение – это дифференциальное уравнение в частных производных, где независимыми переменными являются координаты и время. Учитывая такие аналогии, австрийский физик Эрвин Шредингер получил в 1926 г. основное уравнение квантовой механики для ψ (х, у, z, t)
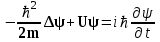, (1.10)
где m – масса частицы, i – мнимая единица, U – потенциальная энергия частицы, Δ‑оператор Лапласа, который представляет собой сумму вторых частных производных по координатам, т.е.
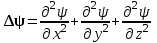(1.11)
Из уравнения Шредингера следует, что конкретный вид волновой функции зависит от потенциальной энергии U, т.е. определяется характером сил, действующих на частицу. Уравнение Шредингера оказалось комплексным (включающим в себя мнимую единицу), поэтому и волновая функция также комплексная, при этом реальный физический смысл имеет квадрат модуля волновой функции (2.5, 2.6), который всегда действителен.
Уравнение Шредингера, будучи дифференциальным уравнением, может иметь множество решений. Из этих решений смысл имеют только те, в которых волновая функция будет однозначной, непрерывной и конечной, что соответствует физической реальности. Эти требования должны относиться и к частным производным от функции по времени и координатам, так как они тоже входят в уравнения Шредингера. Кроме этих требований на волновую функцию накладывается условие нормировки
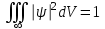, (1.12)
которое следует из того факта, что частица реально существует и обязательно находится где-либо в окружающем пространстве. Поэтому суммарная вероятность нахождения частицы во всем бесконечном пространстве равна единице, т.е. это достоверное событие. Смысл и назначение уравнения Шредингера заключается в том, что если известна волновая функция некоторой частицы в начальный момент времени и известно силовое поле, в котором она движется, то,
решив это уравнение, можно найти волновую функцию и узнать характеристики состояния частицы в последующие моменты времени.
Если силовое поле, в котором движется частица, постоянно во времени, то U не зависит от времени и волновую функцию можно представить в виде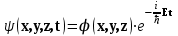
, где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение
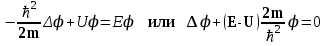(1.13)
Это - уравнение Шредингера для, так называемых, стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.
22.Квантование энергии частицы. Оценка средней энергии для разных l и m.
Для выяснения особенностей решения уравнения Шредингера, рассмотрим поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме». Такой вид потенциала взаимодействия в природе не наблюдается, но он наиболее простой и может демонстрировать основные особенности решения (наиболее близок он к потенциалу, используемому при рассмотрении поведения электрона в металле). Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис.4):
U = в областях 1, 3 для x < 0 и x > a; U = 0 в области 2 для 0> x >a.
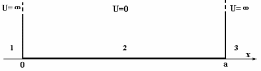
Рис.4. График потенциала одномерной бесконечно глубокой «ямы».
Запишем стационарное уравнение Шредингера для областей 1, 3 , где U=
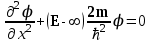, (1.14)
его единственно возможное решение =0. Это означает, что вероятность нахождения частицы в этих областях равна нулю и частица туда проникнуть не может.
Для области 2 стационарное уравнение Шредингера имеет вид
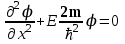, (1.15)
из теории дифференциальных уравнений следует, что его решение имеет вид
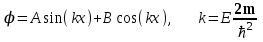. (1.16)
Вследствие требования непрерывности функции , она должна быть равна нулю в точках x=0 и x=a, что следует из решения для областей 1, 3. Отсюда получается, что должны выполняться соотношения Asin(0)+Bcos(0)=0, Asin(ka)+Bcos(ka)=0 и, согласно математике, это будет при B=0 и ka=n, где n-целое число. Необходимое также условие нормировки (1.12) в данной задаче имеет вид
Соотношения неопределенностей позволяют определить границы применимости понятий и законов классической механики к объектам, т.е. возможности одновременного использования понятий координаты и скорости при описании движения. Учитывая, что рх = mvx, можно получить Δх Δvх ≥ h/m, откуда следует, что чем больше масса частицы, тем меньше неопределенность ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для пояснения рассмотрим два примера.
1. Рассмотрим пылинку массой m=10-12 кг и линейными размерами 10-6м и определим для нее неопределенность скорости (неопределенность определения ее координаты примерно равна сотой доли ее размера т.е. Δх = 10-8м). Согласно соотношениям неопределенностей Δvх = h/mΔx = 6,62∙10-34/(10-12∙10-8) = 6,62∙10-14м/с. В результате получается неопределенность измерения скорости, намного меньшая скорости, с которой пылинка может двигаться. Поэтому, в данном случае, скорость и импульс можно определить практически точно и поэтому для пылинки можно использовать понятие траектории и законы классической механики.
2. Рассмотрим электрон, движущийся в атоме водорода. Неопределенность его координаты порядка размера самого атома, т.е. Δx = 10-10м.
Определим Δvх: Δvх = h/mΔx = 6,62∙10-34/(9, 1∙10-31∙10-10) = 7,3∙106м/с. Если рассчитать скорость электрона в атоме согласно классической механики, учитывая, что роль центростремительной силы играет сила Кулона, то скорость получается порядка 2∙106м/с и в данном случае неопределенность измерения скорости оказывается больше самой скорости. Поэтому нельзя говорить о движении электрона в атоме по определенной траектории.
21. Волновая функция. Уравнение Шредингера. Пояснение к нему.
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
Объяснить одновременное наличие корпускулярных и волновых свойств у микрочастиц удалось на основе идей Бора и Луи-де-Бройля в рамках новой теории, называемой волновой или квантовой механикой, созданной Гейзенбергом, Шредингером, Борном и многими другими учеными начала ХХ века. Квантовая механика базируется, как и любая другая физическая теория, на ряде постулатов. Основные постулаты можно представить упрощенно в следующем виде.
1.Движение микрочастиц в пространстве имеет вероятностный (стохастический) характер. Это относится не только к совокупности (ансамблю) частиц, но и к каждой отдельной частице. Согласно этому постулату, микрочастица, находясь в силовых полях или в вакууме (при отсутствии полей), испытывает такое воздействие, что нельзя в любой момент времени определить точно параметры ее движения. Например, нельзя одновременно характеризовать ее траекторию точными значениями координат и скорости или точными значениями энергии и времени какого-либо процесса у частицы.
2.Стохастический характер движения микрочастиц требует применения понятий математики теории вероятности для описания и расчета определенных значений параметров частиц в эксперименте. С точки зрения математики, отсюда следует, что движение таких частиц должно описываться с помощью некоторой «особой» волновой функции, которая должна характеризовать вероятностные особенности микрочастиц. Интерпретацию волновой функции дал в 1926г. немецкий физик Макс Борн следующим образом - волновая функция ψ (х, у, z) характеризует вероятность нахождения частицы в данный момент времени в некоторой точке пространства. Согласно Борну, физический смысл имеет не сама функция, а квадрат модуля волновой функции ψ2, который равен вероятности dP того, что частица будет обнаружена в пределах рассматриваемого малого объема dV.
Формула связи этих понятий имеет вид
dP = ψ2 dV = ψ
2dxdydz . (1.8)
Для совокупности частиц под вероятностью понимают отношение числа частиц в малом объеме к общему числу частиц, а для одной частицы – отношение времени пребывания частицы в малом объеме к общему времени рассмотрения движения частицы.
3.Волновая функция является основной характеристикой состояния микрообъекта, с помощью волновой функции можно рассчитать вероятность пребывания частицы в различных точках пространства в различные моменты времени, а также средние значения различных ее параметров. Соответственно вероятностному смыслу волновой функции и используя формулы теории вероятности, средние значения параметров находятся путем усреднения соответствующих операторов с помощью волновой функции. Например среднее значение для модуля радиуса-вектора частицы
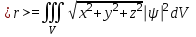. (1.9)
Так как в физических экспериментах определяются именно средние значения параметров частицы, то можно говорить, что состояние частицы полностью задается ее волновой функцией.
4.Вид волновой функции зависит от типа частицы и от внешних силовых полей, действующих на частицу. Вид функции находится с помощью специального дифференциального уравнения, называемого уравнением Шредингера.
5.Если в эксперименте наблюдается суперпозиция (объединение) микрочастиц, описываемых разными волновыми функциями, то объединенный ансамбль этих частиц будет описываться суммой их волновых функций. Например, если при интерференции микрочастиц на двух щелях, их можно по отдельности описать двумя функциями ψ1 и ψ2, тогда совокупность этих частиц в районе экрана должна описываться функцией ψ = ψ1+ψ2. Так как вероятность распределения частиц на экране dP определяется квадратом модуля волновой функции, то получаем dP ψ2 = ψ12 + 2ψ1ψ2 + ψ22. Отсюда следует, что распределение зависит не только от простого сложения вероятностей двух независимых ансамблей ψ12 + ψ22, но и от результата их специфичного квантового «взаимодействия» 2ψ1ψ2, вследствие чего и наблюдается интерференция частиц.
Имеется еще ряд постулатов, но они имеют более частный характер, о некоторых из них будет сказано далее.
Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния.
Для расчета волновой функции необходимо иметь уравнение, которое позволяло бы для любого момента времени определить эту функцию с учетом действующих на частицу внешних силовых полей. Чтобы искомое уравнение учитывало волновые свойства микрочастиц, необходимо чтобы оно по форме было волновым уравнением, подобно тем, которые описывают звуковые или электромагнитные волны. Известно, что для плоской волны, распространяющейся вдоль оси х, волновое уравнение – это дифференциальное уравнение в частных производных, где независимыми переменными являются координаты и время. Учитывая такие аналогии, австрийский физик Эрвин Шредингер получил в 1926 г. основное уравнение квантовой механики для ψ (х, у, z, t)
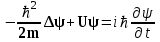, (1.10)где m – масса частицы, i – мнимая единица, U – потенциальная энергия частицы, Δ‑оператор Лапласа, который представляет собой сумму вторых частных производных по координатам, т.е.
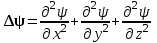(1.11)Из уравнения Шредингера следует, что конкретный вид волновой функции зависит от потенциальной энергии U, т.е. определяется характером сил, действующих на частицу. Уравнение Шредингера оказалось комплексным (включающим в себя мнимую единицу), поэтому и волновая функция также комплексная, при этом реальный физический смысл имеет квадрат модуля волновой функции (2.5, 2.6), который всегда действителен.
Уравнение Шредингера, будучи дифференциальным уравнением, может иметь множество решений. Из этих решений смысл имеют только те, в которых волновая функция будет однозначной, непрерывной и конечной, что соответствует физической реальности. Эти требования должны относиться и к частным производным от функции по времени и координатам, так как они тоже входят в уравнения Шредингера. Кроме этих требований на волновую функцию накладывается условие нормировки
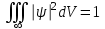, (1.12)которое следует из того факта, что частица реально существует и обязательно находится где-либо в окружающем пространстве. Поэтому суммарная вероятность нахождения частицы во всем бесконечном пространстве равна единице, т.е. это достоверное событие. Смысл и назначение уравнения Шредингера заключается в том, что если известна волновая функция некоторой частицы в начальный момент времени и известно силовое поле, в котором она движется, то,
решив это уравнение, можно найти волновую функцию и узнать характеристики состояния частицы в последующие моменты времени.
Если силовое поле, в котором движется частица, постоянно во времени, то U не зависит от времени и волновую функцию можно представить в виде
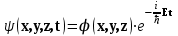, где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение 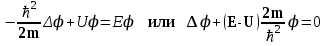(1.13)Это - уравнение Шредингера для, так называемых, стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.
22.Квантование энергии частицы. Оценка средней энергии для разных l и m.
Для выяснения особенностей решения уравнения Шредингера, рассмотрим поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме». Такой вид потенциала взаимодействия в природе не наблюдается, но он наиболее простой и может демонстрировать основные особенности решения (наиболее близок он к потенциалу, используемому при рассмотрении поведения электрона в металле). Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис.4):
U = в областях 1, 3 для x < 0 и x > a; U = 0 в области 2 для 0> x >a.
Рис.4. График потенциала одномерной бесконечно глубокой «ямы».
Запишем стационарное уравнение Шредингера для областей 1, 3 , где U=
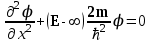, (1.14)его единственно возможное решение =0. Это означает, что вероятность нахождения частицы в этих областях равна нулю и частица туда проникнуть не может.
Для области 2 стационарное уравнение Шредингера имеет вид
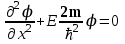, (1.15)из теории дифференциальных уравнений следует, что его решение имеет вид
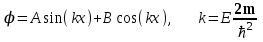. (1.16)Вследствие требования непрерывности функции , она должна быть равна нулю в точках x=0 и x=a, что следует из решения для областей 1, 3. Отсюда получается, что должны выполняться соотношения Asin(0)+Bcos(0)=0, Asin(ka)+Bcos(ka)=0 и, согласно математике, это будет при B=0 и ka=n, где n-целое число. Необходимое также условие нормировки (1.12) в данной задаче имеет вид