Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 228
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Интерференция света в тонких пленках или полосы ровного наклона.
6.Дифракция Френеля на круглом отверстии и диске.
7.Дифракция Фраунгофера на прямоугольной щели.
8. Дисперсия и разрешающая сила спектрального прибора.
Оптическая активность веществ. @
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера.
4. 3. Поляризация света при двойном лучепреломлении.
6. 1. Характеристики теплового излучения. @
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
28. Состав ядра. Характеристики ядра. Размеры ядер.
х = Е0хcos (ωt+1)
Еy = Е0ysin (ωt+2)
Уравнение траектории, которую описывает конец результирующего вектора Е при сложении взаимно перпендикулярных гармонических колебаний одинаковой частоты имеет следующий вид:
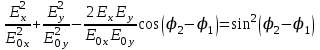
г
де Е0х и Е0у – амплитуды складываемых колебаний, 2 - 1 – разность фаз колебаний. При произвольном постоянном значении разности фаз траектория, описываемая результирующим вектором Е является эллипсом (рис. 4.3 а), размеры которого зависят от амплитуд Е0х и Е0у складываемых колебаний и разности их начальных фаз 2 - 1. Такой свет называется эллиптически поляризованным.
Если разность фаз 2 - 1 = (2m+1)π/2, где m= 0,±1,±2, …и амплитуды Е0х = Е0у , то траектория результирующего вектора Е представляет собой окружность (рис. 4.3 б), а свет
называется поляризованным по кругу (или циркулярно поляризованным):
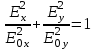
При разности фаз 2 - 1 = mπ, где m = 0, ±1, ±2,… эллипс вырождается в отрезок прямой (рис. 4.3 в):
Еу = ±(Е0у/Е0х)Ех
Такой свет называется линейно поляризованным (плоско поляризованным).
Свет от естественных источников может приобрести частичную или полную поляризацию при взаимодействии с веществом. Поляризация света состоит в выделении из светового пучка колебаний определенного направления. Для этой цели используют специальные устройства, называемые поляризаторами.
E2) ,то для интенсивности света I, вышедшего из анализатора получаем:
I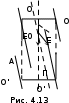
= I0 cos2,
где I0 – интенсивность света, падающего на анализатор. Этот закон называется законом Малюса. Если естественный свет с интенсивностью Iест проходит последовательно сквозь поляризатор и анализатор, то выходящий свет имеет интенсивность
.
При = 0 (плоскости поляризатора и анализатора параллельны) интенсивность максимальна Imax = 1/2 Iест, при = π/2 (плоскости поляризатора и анализатора взаимно перпендикулярны) интенсивность минимальна Imin = 0.
Для анализа поляризованности света анализатор нужно вращать вокруг луча, если при этом можно найти такое положение, при котором свет сквозь него не проходит (интенсивность становится равной нулю), то такой свет полностью поляризован; если при вращении анализатора интенсивность света не изменяется, такой свет будет естественный.
При пропускании плоско поляризованного света через некоторые вещества наблюдается вращение плоскости поляризации. Вещества, способные вращать плоскость поляризации, называются оптически активными. Оптической активностью могут обладать кристаллы (кварц, киноварь), жидкости (скипидар, винная кислота), растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, яблочной кислоты, спиртовые растворы камфоры, стрихнина). Оптическую активность проявляют многие природные соединения: белки, углеводы, гормоны, эфирные масла.
Угол поворота плоскости поляризации для оптически активных кристаллов и чистых жидкостей
= αd
где α –постоянная вращения, угол поворота плоскости поляризации слоем вещества единичной толщины; d – расстояние, пройденное светом в оптически активном веществе. Постоянная вращения зависит от природы вещества, температуры и длины волны света. Зависимость α от λ, называется дисперсией вращения. Наибольшей оптической активностью обладают некоторые жидкие кристаллы.
Угол поворота плоскости поляризации для оптически активных растворов (закон Био)
= [α] с d
где [α] – удельное вращение, с – массовая концентрация оптически активного вещества, d – расстояние, пройденное светом в оптически активном веществе.
Оптическая активность обуславливается как асимметричным строением молекул вещества, так и расположением частиц в кристаллической решетке. В зависимости от направления вращения плоскости поляризации оптические вещества делятся на
право- и левовращающие. В первом случая осуществляется вращение плоскости вправо (по часовой стрелке), во втором – влево (против часовой стрелке).
О
О
Еm
E1
E2
б)
ω2=ω1
О
О'
О
О'
Еm
E1
E2
в)
ω2>ω1
Δ/2
Рис. 4.18
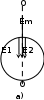
Вращение плоскости поляризации объяснено О. Френелем (1823г.). Он предложил (рис. 4.18 а) линейно поляризованную монохроматическую волну представить в виде комбинации двух одновременно распространяющихся поляризованных по кругу монохроматических волн, векторы напряженностей Е1 и Е2 у которых равны половине амплитуды вектора Е и вращаются во взаимно противоположных направлениях с одинаковыми угловыми скоростями (рис. 4.18 б). В оптически активной среде волны Е
1 и Е2 распространяются с разными фазовыми скоростями. На выходе из слоя толщиной l волны Е1 и Е2 складываются (рис.4.18 в), но между ними возникает сдвиг фаз Δ, пропорциональный толщине слоя l. Плоскость поляризации на выходе (О'О') оказывается повернутой относительно плоскости поляризации на входе (ОО) на угол поворота Δ/2.
Закон Фарадея.
М. Фарадеем (1845г.) было установлено, что вещества, не обладающие естественной оптической активностью, приобретают ее под действием магнитного поля. Это явление называется эффектом Фарадея или магнитное вращение плоскости поляризации. Угол поворота плоскости поляризации пропорционален напряженности магнитного поля Н, длине пути света в веществе l.
= VHl
где V – постоянная Верде (или удельным магнитным вращением), которая зависит от природу вещества и длины волны света. Направление магнитного вращения плоскости поляризации определяется направлением магнитного поля и не зависит от направления распространения луча. Так, если отразить луч света с помощью зеркала и заставить пройти через намагниченное вещество еще раз только в обратном направлении, то угол поворота плоскости поляризации удвоится. Этим эффект Фарадея отличается от вращения плоскости поляризации света в естественных оптически активных средах.
Магнитное вращение плоскости поляризации обусловлено возникающей под действием магнитного поля прецессией электронных орбит. Оптически активное вещество под действием магнитного поля приобретает дополнительную способность вращать плоскость поляризации и угол поворота будет равен сумме углов поворота при естественной и искусственной оптических активностей.
Явления вращения плоскости поляризации лежат в основе метода определения концентрации растворов оптически активных веществ. Этот метод называется поляриметрией, а при определении содержания сахара сахариметрией. Они успешно используются в пищевой промышленности, в медицине, при исследовании биополимеров.
10.Методы получения поляризованного света. Закон Брюстера. 2е лучепреломление.
Еy = Е0ysin (ωt+2)
Уравнение траектории, которую описывает конец результирующего вектора Е при сложении взаимно перпендикулярных гармонических колебаний одинаковой частоты имеет следующий вид:
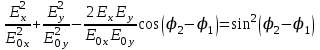
г
де Е0х и Е0у – амплитуды складываемых колебаний, 2 - 1 – разность фаз колебаний. При произвольном постоянном значении разности фаз траектория, описываемая результирующим вектором Е является эллипсом (рис. 4.3 а), размеры которого зависят от амплитуд Е0х и Е0у складываемых колебаний и разности их начальных фаз 2 - 1. Такой свет называется эллиптически поляризованным.Если разность фаз 2 - 1 = (2m+1)π/2, где m= 0,±1,±2, …и амплитуды Е0х = Е0у , то траектория результирующего вектора Е представляет собой окружность (рис. 4.3 б), а свет
называется поляризованным по кругу (или циркулярно поляризованным):
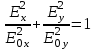
При разности фаз 2 - 1 = mπ, где m = 0, ±1, ±2,… эллипс вырождается в отрезок прямой (рис. 4.3 в):
Еу = ±(Е0у/Е0х)Ех
Такой свет называется линейно поляризованным (плоско поляризованным).
Свет от естественных источников может приобрести частичную или полную поляризацию при взаимодействии с веществом. Поляризация света состоит в выделении из светового пучка колебаний определенного направления. Для этой цели используют специальные устройства, называемые поляризаторами.
Анализ плоскополяризованного света. Закон Малюса.
Глаз человека не может отличить поляризованный свет от естественного, поэтому для анализа поляризованного свет необходимо использовать поляризаторы, которые в этом случае называются анализаторами. Все ранее перечисленные поляризующие устройства можно использовать для анализа поляризации света. Анализировать поляризованность света первым предложил французский физик Э. Малюс (1775-1812), установив закон изменения интенсивности поляризованного света.
Возьмем в качестве поляризатора и анализатора дихроичный кристалл турмалин (рис. 4.12). Пусть естественный свет падает перпендикулярно оптической оси ОО' поляризатора П. Через поляризатор свободно пройдут колебания светового вектора, параллельные плоскости поляризатора. Колебания светового вектора, перпендикулярные плоскости поляризации, полностью поглотятся кристаллом турмалина. Ранее уже говорилось о том, что любое колебание вектора Ес можно представить как результат сложения двух взаимно перпендикулярных векторов Ех и Еу (рис. 4. 2), а так как колебания вектора Ес естественного света хаотичны и равновероятны, то интенсивность света, прошедшего через поляризатор, равна половине интенсивности падающего естественного света:
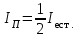
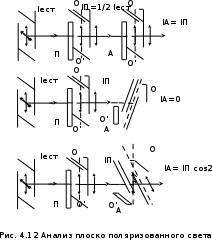
Если плоско поляризованный свет падает на анализатор А (рис. 4.13), то через него пройдет только составляющая, параллельная главной плоскости анализатора:
Е = Е0 cos,
где - угол между плоскостями поляризации поляризатора и анализатора. Так как интенсивность света пропорциональна квадрату амплитуды (I
E2) ,то для интенсивности света I, вышедшего из анализатора получаем: I
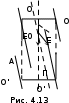= I0 cos2,где I0 – интенсивность света, падающего на анализатор. Этот закон называется законом Малюса. Если естественный свет с интенсивностью Iест проходит последовательно сквозь поляризатор и анализатор, то выходящий свет имеет интенсивность
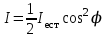.При = 0 (плоскости поляризатора и анализатора параллельны) интенсивность максимальна Imax = 1/2 Iест, при = π/2 (плоскости поляризатора и анализатора взаимно перпендикулярны) интенсивность минимальна Imin = 0.
Для анализа поляризованности света анализатор нужно вращать вокруг луча, если при этом можно найти такое положение, при котором свет сквозь него не проходит (интенсивность становится равной нулю), то такой свет полностью поляризован; если при вращении анализатора интенсивность света не изменяется, такой свет будет естественный.
Оптическая активность веществ. @
При пропускании плоско поляризованного света через некоторые вещества наблюдается вращение плоскости поляризации. Вещества, способные вращать плоскость поляризации, называются оптически активными. Оптической активностью могут обладать кристаллы (кварц, киноварь), жидкости (скипидар, винная кислота), растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, яблочной кислоты, спиртовые растворы камфоры, стрихнина). Оптическую активность проявляют многие природные соединения: белки, углеводы, гормоны, эфирные масла.
Угол поворота плоскости поляризации для оптически активных кристаллов и чистых жидкостей
= αd
где α –постоянная вращения, угол поворота плоскости поляризации слоем вещества единичной толщины; d – расстояние, пройденное светом в оптически активном веществе. Постоянная вращения зависит от природы вещества, температуры и длины волны света. Зависимость α от λ, называется дисперсией вращения. Наибольшей оптической активностью обладают некоторые жидкие кристаллы.
Угол поворота плоскости поляризации для оптически активных растворов (закон Био)
= [α] с d
где [α] – удельное вращение, с – массовая концентрация оптически активного вещества, d – расстояние, пройденное светом в оптически активном веществе.
Оптическая активность обуславливается как асимметричным строением молекул вещества, так и расположением частиц в кристаллической решетке. В зависимости от направления вращения плоскости поляризации оптические вещества делятся на
право- и левовращающие. В первом случая осуществляется вращение плоскости вправо (по часовой стрелке), во втором – влево (против часовой стрелке).
О
О
Еm
E1
E2
б)
ω2=ω1
О
О'
О
О'
Еm
E1
E2
в)
ω2>ω1
Δ/2
Рис. 4.18
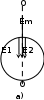
Вращение плоскости поляризации объяснено О. Френелем (1823г.). Он предложил (рис. 4.18 а) линейно поляризованную монохроматическую волну представить в виде комбинации двух одновременно распространяющихся поляризованных по кругу монохроматических волн, векторы напряженностей Е1 и Е2 у которых равны половине амплитуды вектора Е и вращаются во взаимно противоположных направлениях с одинаковыми угловыми скоростями (рис. 4.18 б). В оптически активной среде волны Е
1 и Е2 распространяются с разными фазовыми скоростями. На выходе из слоя толщиной l волны Е1 и Е2 складываются (рис.4.18 в), но между ними возникает сдвиг фаз Δ, пропорциональный толщине слоя l. Плоскость поляризации на выходе (О'О') оказывается повернутой относительно плоскости поляризации на входе (ОО) на угол поворота Δ/2.
Закон Фарадея.
М. Фарадеем (1845г.) было установлено, что вещества, не обладающие естественной оптической активностью, приобретают ее под действием магнитного поля. Это явление называется эффектом Фарадея или магнитное вращение плоскости поляризации. Угол поворота плоскости поляризации пропорционален напряженности магнитного поля Н, длине пути света в веществе l.
= VHl
где V – постоянная Верде (или удельным магнитным вращением), которая зависит от природу вещества и длины волны света. Направление магнитного вращения плоскости поляризации определяется направлением магнитного поля и не зависит от направления распространения луча. Так, если отразить луч света с помощью зеркала и заставить пройти через намагниченное вещество еще раз только в обратном направлении, то угол поворота плоскости поляризации удвоится. Этим эффект Фарадея отличается от вращения плоскости поляризации света в естественных оптически активных средах.
Магнитное вращение плоскости поляризации обусловлено возникающей под действием магнитного поля прецессией электронных орбит. Оптически активное вещество под действием магнитного поля приобретает дополнительную способность вращать плоскость поляризации и угол поворота будет равен сумме углов поворота при естественной и искусственной оптических активностей.
Явления вращения плоскости поляризации лежат в основе метода определения концентрации растворов оптически активных веществ. Этот метод называется поляриметрией, а при определении содержания сахара сахариметрией. Они успешно используются в пищевой промышленности, в медицине, при исследовании биополимеров.
10.Методы получения поляризованного света. Закон Брюстера. 2е лучепреломление.