Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 993
Скачиваний: 24
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тест №3
-
Какая из следующих функций возрастает на , :
A) xarctgx B) sin(2x1)
 C) D) ln(1 x2 )
C) D) ln(1 x2 )-
Найти интервалы возрастания функции:
А) (0;2) В) (2;+∞)
y(x)
4
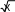 x 2
x 2С) (-∞;-2) (0;2) D) (-∞;-2) (2;+∞)
-
Найдите точку минимума функции
f(x)
3x2 4x 4 :
x2 x 1
-
x 2 -
x 4 -
x 0 -
x 6
-
Найти и охарактеризовать точки экстремума функции f(x) (x2 9)2 :
-
x 3 ,
x 3
-
точки локального максимума
-
x 3 ,
x 3
-
точки локального максимума;
x 0
-
точка локального
минимума
-
x 3 ,
x 3
-
точки локального минимума
-
x 3 ,
x 3
-
точки локального минимума;
x 0
-
точка локального
максимума
-
 Найти наименьшее значение функции
Найти наименьшее значение функции
y(x) на [0; 3].
-
-1 B) не достигается
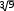 С) D) 0
С) D) 0
-
Найти вторую производную функции
f(x) xcos2x 5 .
A) f (x) sin(2x 5) xcos2x 5
B) f (x) 4cos(2x 5) 4xsin2x 5
C) f (x) 4sin(2x 5) 4xcos2x 5
D) f (x) sin(2x 5) xcos2x 5
-
Найдите интервалы выпуклости вниз функции f(x) x4 2x3 7 :
A) (, 1) B) (0, 1)
C) (, 0) ∪ (1, )
D) (0, )
-
Найти точки перегиба графика функции
y(x) x3e4x
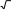 A) x 33 ;
A) x 33 ;4
x 3 3
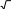 4
4-
x 0
-
x 0;
x 3
4
-
x 0;
x 33 ;
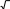 4
4x 3 3
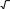 4
4-
Вычислите значение производной функции
у 3 в точке .

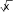 х
х-
Найдите производную функции
у х2 sin x.
1) 2хcos x
3) 2хsin x х2 cos x
2) 2хsin x х2 cos x 4) 2хcos x
Ответы на тесты
| Тест №1 | ||||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | С | В, С | В, С | Главная часть приращения функции в точке a; f(a) dx | B, D | Дифференци руемы; | A | A | D | B |
| Тест №2 | ||||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | A | A | B | D | C | (a; b); ; f(c) (b a | ) 1-3 | B | 1-2; | C |
| | | | | | | | 2-2 | | 2-1; | |
| | | | | | | | 3-1 | | 3-3 | |
| | | | | | | | 4-4 | | | |
| Тест №3 | ||||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | C | F | D | D | D | C | B | D | -49 | 3 |