Промежуточные точки на дуге окружности А₀А₃ определяют по­ложение концов векторов тока I₁ при различных нагрузках в двига­тельном режиме (0 < s ≤ 1). Ось абсцисс диаграммы ОB является ли­нией первичной мощности P₁. Линией электромагнитной мощности Р_эм или электромагнитных моментов М_эм является линия А₀А₂. Ли­нией полезной мощности на валу (вторичной мощности Р₂) является линия А'₀А₃. По круговой диаграмме для тока статора, которому со­ответствует точка А на окружности, можно рассчитать необходи­мые для построения рабочих характеристик данные:

ток статора, А, I₁ = m_I |OA|;

ток ротора, А, I'₂ = m_I |A₀A|;

первичную мощность, Вт, P₁ = m_р |AN|, где AN ┴ ОВ;

электромагнитную мощность, Вт, Р_эм = m_р |АС|, где АС ┴ A₀F;

электромагнитный момент М_эм = m_м |АС|;

полезную мощность, Вт, Р₂ = m_р |АЕ|;

КПД |АЕ| / |AN|;

коэффициент мощности cos φ = cos < AOB₁;

скольжение двигателя |DС| / |АС|.

Для построения рабочих характеристик вначале находят поло­жение на окружности точки А_н, которая соответствует номинально­му режиму работы. Для этого, исходя из заданной номинальной мощности Р_2ном, рассчитывают длину отрезка |E'F_н| = P_2ном / m_p и от­кладывают на линии F₁F' ┴ A₀F от точки ее пересечения Е' с линией полезной мощности А'₀А₃. Через точку F_н проводят F_нA_н || А'₀А₃. Точ­ки пересечения F_HA_H с окружностью А_н и А'_н определяют положение концов вектора тока I₁ при мощности Р_2ном. Точка А_н, ближайшая к А'₀, соответствует номинальному режиму, точка А'_Н — режиму неу­стойчивой работы двигателя (при s > s_кp).

Наметив на дуге А₀А_н несколько точек а₁, а₂, а₃, ..., определяют соответствующие каждой из них данные I₁, Р₁, Р₂, соs φ, η, М, s.

Из круговой диаграммы можно найти также приближенное значение кратности максимального момента М_mах. Оно будет несколь­ко занижено, так же как и в аналитическом расчете без учета изме­нения параметров от насыщения полями рассеяния и от действия эффекта вытеснения тока.

Расчет рабочих характеристик по круговой диаграмме связан с определенными погрешностями при выполнении графических работ. Некоторое уточнение может дать сочетание графического метода и элементов аналитического. Например, I

---

₁, I₂ и cos φ определяют по круговой диаграмме, а суммы потерь, Р₂, Р₁, s и η - расчетным путем, используя данные круговой диаграммы. В этом случае можно также учесть дополнительные потери, которые при построении круговой диаграммы не принимают во внимание [6].

Такая методика расчета иногда применяется на практике. Одна­ко все более широкое распространение ЭВМ делает аналитический метод расчета рабочих характеристик более предпочтительным.
9.13. РАСЧЕТ ПУСКОВЫХ ХАРАКТЕРИСТИК

---

Учет эффекта вытеснения тока. С увеличением частоты тока в стержнях обмотки короткозамкнутого ротора возникает эффект вы­теснения тока, в результате которого плотность тока в верхней час­ти стержней возрастает, а в нижней уменьшается, при этом активное сопротивление ротора увеличивается, а индуктивное уменьшается. Изменение сопротивлений ротора влияет на пусковые характери­стики машины.

В большинстве случаев эффект вытеснения тока в обмотках короткозамкнутых роторов играет положительную роль, так как уве­личивает начальные моменты двигателей. Это широко используют при проектировании асинхронных машин, выполняя роторы с глу­бокими прямоугольными или фигурными пазами или с двойной беличьей клеткой, в которых эффект вытеснения тока проявляется особенно сильно. Однако неравномерное распределение плотности тока по сечению стержня ротора может привести и к нежелатель­ным последствиям. Например, при неудачно выбранных размерных соотношениях стержней чрезмерно возрастающая в пусковых режи­мах плотность тока в их верхних участках может вызвать неравно­мерное тепловое удлинение стержней и их изгиб. При этом стержни разрывают усики пазов и выгибаются в воздушный зазор, что неиз­бежно приводит к выходу двигателя из строя. В связи с этим правильный учет влияния эффекта вытеснения тока является необходимым при проектировании асинхронных машин с короткозамкнутыми роторами.

В расчетах удобнее определять не непосредственно активное и индуктивное сопротивления стержней при неравномерной плотно­сти тока, а их относительные изменения под действием эффекта вы­теснения тока. Эти изменения оценивают коэффициентами k_r и k_д. Коэффициент k_r показывает, на сколько увеличилось активное со­противление пазовой части стержня r_cξ при неравномерной плотно­сти тока в нем по сравнению с его сопротивлением r_с при одинако­вой плотности по всему сечению стержня:
k_r = r_cξ / r_с. (9.238)
Коэффициент демпфирования k_д показывает, как уменьшилась магнитная проводимость λ_пξ участка паза, занятого проводником с током, при действии эффекта вытеснения тока по сравнению с про­водимостью того же участка, но при равномерной плотности тока в стержне
k_д = λ'_пξ / λ'_п (9.239)
Аналитическими выражениями, определяющими k

---

_r и k_д, полу­ченными для прямоугольных стержней при допущениях о постоян­стве удельного сопротивления материала стержня по всей площади его поперечного сечения, бесконечности магнитной проницаемости стали магнитопровода и прямолинейности магнитных линий потока рассеяния в пазу, являются
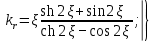(9.240)
В этих выражениях ξ, так называемая «приведенная высота» стержня, — величина безразмерная, значение которой определяется по формуле
ξ = 2 πh_c 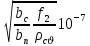(9.241)
где h_с — высота стержня в пазу, м: h_с = h_п - (h_ш + h'_ш); b_с и b_п — ширина стержня и ширина паза, м. При расчете роторов со вставными стерж­нями принимают b_с = 0,96 b_п ; в роторах с литой обмоткой — b_c = b_п; f₂ — частота тока в роторе в расчетном режиме, Гц; р_сυ — удельное сопротивление материала стержня при расчетной температуре, Ом-м.

Для двигателей общего назначения с медными вставными стерж­нями короткозамкнутого ротора при расчетной температуре 75° С (ρ_с75 = 10^-6/47 Ом м, см. табл. 5.1) из (9.241) имеем
ξ = 96,32 h_c 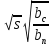(9.242)
При расчетной температуре 115° С (ρ_c115 = 10^-6 /41 Ом м)
ξ = 89,96 h_c 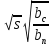(9.243)
При литой алюминиевой обмотке ротора при расчетных температypax 75° С (ρ_с75 = 10^-6/21,5 Ом м) и 115° С (ρ_с115 = 10^-6/20,5 Ом м) соответственно имеем
ξ = 61,15 h_c 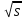(9.244)
ξ = 63,61 h_c 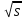(9.245)
Анализ зависимостей (9.240) показывает, что при ξ ≤ 1 эффект вы­яснения тока практически не влияет на сопротивления стержней. Это является критерием необходимости его учета при проектировании.

В расчетах условно принимают, что при действии эффекта вы­теснения ток ротора распределен равномерно, но не по всему сече­нию стержня, а лишь по его верхней части, ограниченной высотой h

---

_r, имеющей сечение q_r и сопротивление r_cξ = r_c q_c /q_r; h_r называют глубиной проникновения тока в стержень. Для прямоугольных стерж­ней h_r = h_с/ k_r.

При определении λ_пξ аналогично принимают, что ток равномер­но распределен по верхней части сечения стержня высотой h_x.

В практических расчетах для определения k_r, и k_д пользуются не аналитическими зависимостями (9.240), а построенными на их осно­ве кривыми φ(ξ) и φ'(ξ) (рис. 9.57 и 9.58). Принятые при выводе (9.240) допущения приводят к положению, что на глубину проник­новения не влияют высота и конфигурация стержня. Это позволяет использовать (9.240) и кривые φ(ξ) и φ'(ξ) для определения k_r и k_д в стержнях различных конфигураций. Расчет проводят в следующей последовательности. По полной высоте стержня, частоте тока и уде­льному сопротивлению материала стержня из табл. 5.1 по (9.241) определяют функцию ξ, в соответствии с которой по кривым рис. 9.57 находят функцию φ, а по кривым рис. 9.58 — функцию φ'.

Далее определяют глубину проникновения тока
h_r = h_c / (1+φ) (9.246)
и коэффициент k_д = φ'.

Коэффициент k_r определяют по отношению площадей всего се­чения стержня и сечения, ограниченного высотой h_r, т. е.
k_r = q_c/q_r. (9.247)


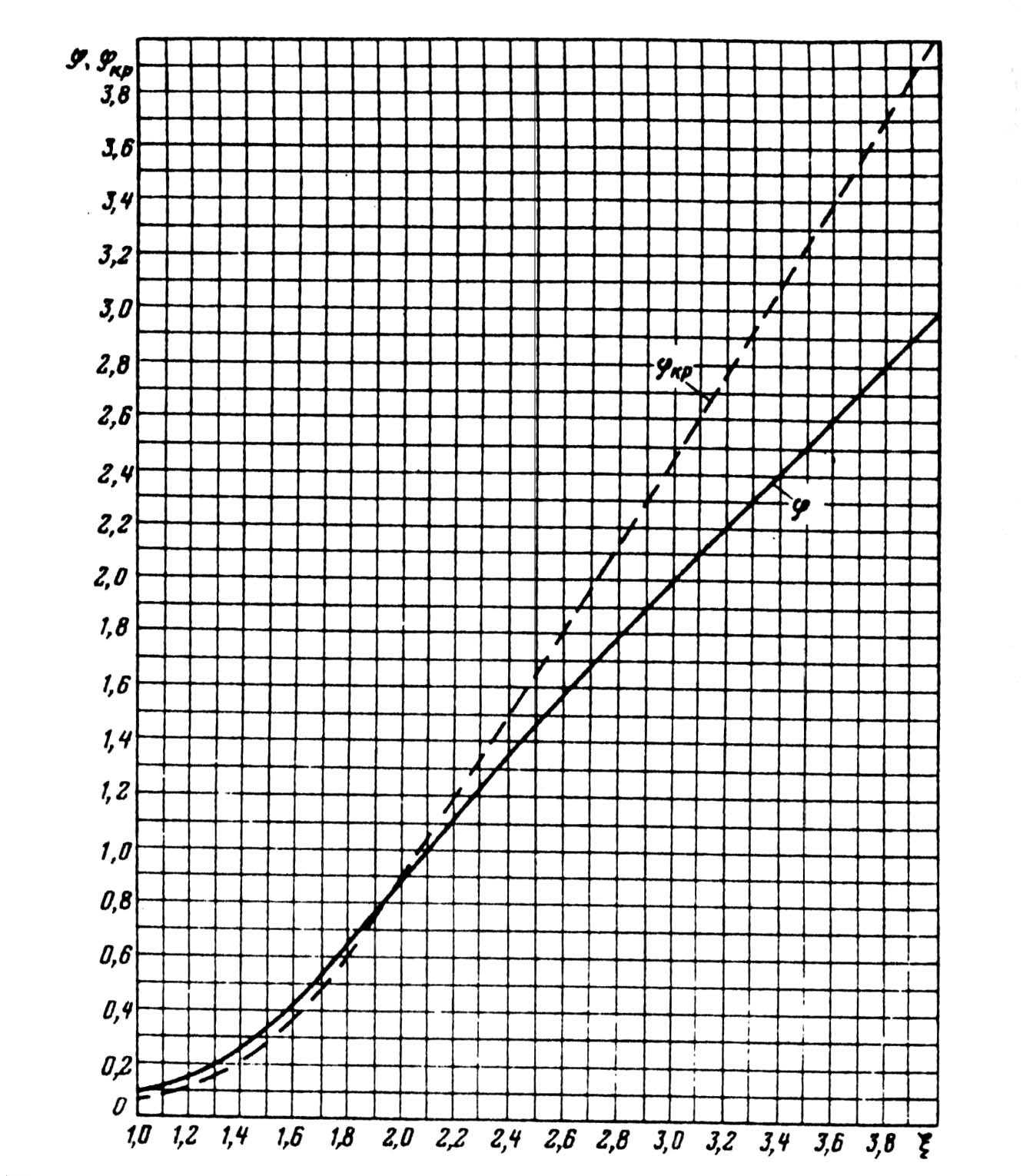
Рис. 9.57. Кривые φ и φ_кр в функции “приведенной высоты” ξ (φ = ξ – 1

при ξ > 4 и φ = 0,89ξ⁴ при ξ < 1 )


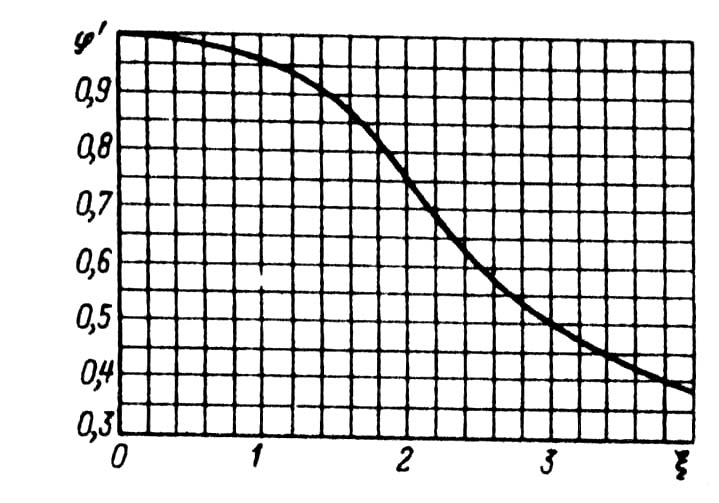
Рис. 9.58. Зависимость φ' от “приведенной высоты”

ξ: при ξ > 4 φ = 3/2 ξ

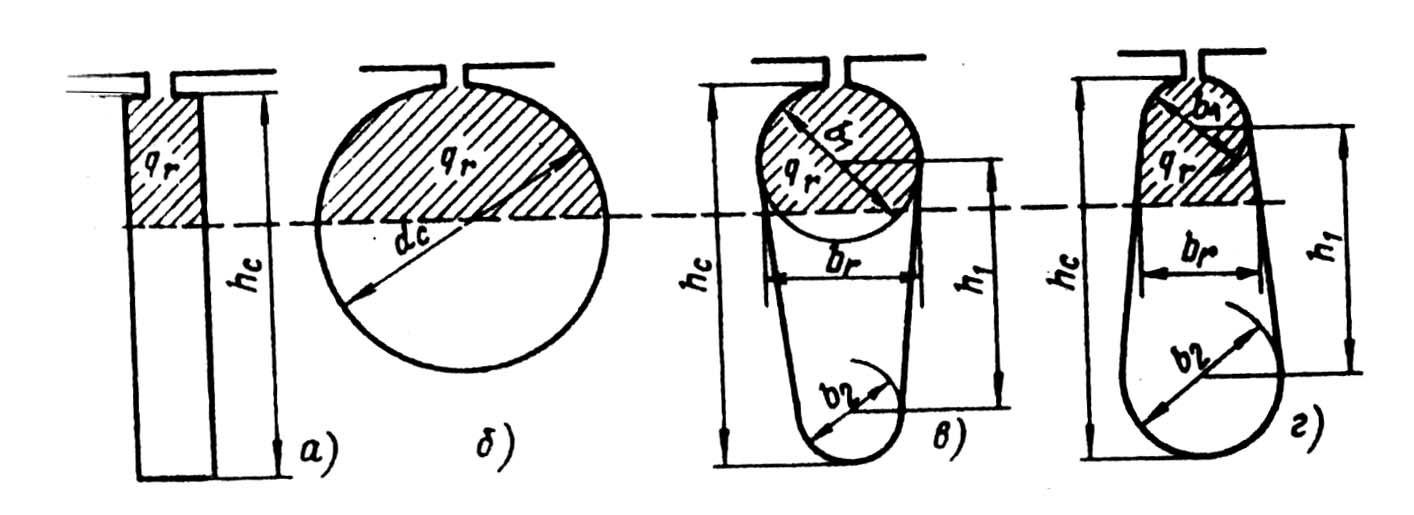
Рис. 9.59. К расчету К_г в стержнях различной конфигурации:

h_г — расчетная глубина проникновения тока
По значениям k_r и k_д можно найти сопротивление пазовой части стержня обмотки ротора и коэффициент магнитной проводимости участка паза ротора, занятого стержнем с током:
r_cξ = k_rr_c; (9.248)

λ'_пξ = k_дλ'_п (9.249)
Для определения k_r в стержнях некоторых наиболее распростра­ненных конфигураций используют заранее полученные расчетные формулы.

Для прямоугольных стержней (рис. 9.59, а)
k_r = q_с / q

---

Смотрите также файлы

• Контрольная работа по дисциплине Мировая экономика Вариант 3 Магнитогорск 2021 г. Проблемы интеграции в мировой торговле.docx

• Кратко расскажите о революции в России 1917 г., ее причинах и последствиях.docx

• Аутизм. Особенности работы с детьми с расстройством аутистического спектра. Видео Мир глазами аутиста.pdf

• Первая помощь содержание, объем, организационные и юридические основы, общие принципы оказания.doc

• Результат попытки теста.docx