Файл: Курсовая работа по дисциплине Качественные и количественные методы педагогических и психологических исследований.docx

ПРИЛОЖЕНИЕ 1

Расчет Критерия Манна-Уитни. где T_x - наибольшая сумма рангов, n_x - наибольшая из объемов выборок n₁ и n₂. Сравнение результатов показывает, что значения выборки 1 несколько выше, чем выборки 2. Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между значениями существенной. Гипотезы: Н0: Различия между уровнями развития связной речи детей в выборках 1 и 2 незначительны. Н1: Различия между уровнями развития связной речи детей в выборках 1 и 2 значительны. Решение. Проранжируем представленную таблицу. При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания. Так как в матрице имеются связанные ранги (одинаковый ранговый номер) 1-го ряда, произведем их переформирование. Переформирование рангов производиться без изменения важности ранга, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n = 20). Переформирование рангов производится в таблице.

Номера мест в упорядоченном ряду		Расположение факторов по оценке эксперта	Новые ранги
1		4.5	1
2		5.5	2
3		7.5	3.5
4		7.5	3.5
5		8	6
6		8	6
7		8	6
8		8.5	9.5
9		8.5	9.5
10		8.5	9.5
11		8.5	9.5
12		9	13
13		9	13
14		9	13
15		9.5	15.5
16		9.5	15.5
17		10	17
18		10.5	18
19		12	19
20		13	20
	Используя предложенный принцип ранжирования, получим

---

следующую таблицу рангов.

X		Ранг X	Y	Ранг Y
4.5		1	5.5	2
8.5		9.5	7.5	3.5
8.5		9.5	7.5	3.5
8.5		9.5	8	6
9		13	8	6
9.5		15.5	8	6
9.5		15.5	8.5	9.5
10		17	9	13
12		19	9	13
13		20	10.5	18
Сумма		129.5	Сумма	80.5
	Этих данных достаточно, чтобы воспользоваться формулой расчёта

эмпирического значения критерия: Гипотеза H₀ о незначительности различий между выборками принимается, если U_кр < U_эмп. В противном случае H0 отвергается и различие определяется как существенное. где U_kp - критическая точка, которую находят по таблице Манна-Уитни. Найдем критическую точку Ukp. По таблице находим U_kp(0.05) = 23 По таблице находим U_kp(0.01) = 16

---

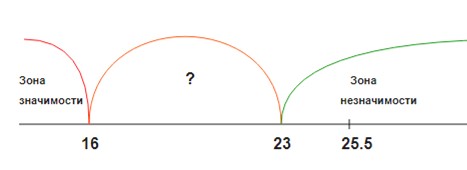
Так как Ukp эмп — принимаем нулевую гипотезу, т.е.различия в уровнях развития связной речи дошкольников с ТНР в выборках можно считать не значительными.

1   2   3   4   5   6   7   8

---

ПРИЛОЖЕНИЕ 2

Расчёт Т-Критерия Вилкоксона Гипотезы. H₀: Показатели уровня развития связной речи детей старшего дошкольного возраста с ТНР после проведения опыта меньше значений показателей до апробации программы. H₁: Показатели уровня развития связной речи детей старшего дошкольного возраста после проведения опыта больше значений показателей до апробации программы.

Код имени испытуемого		До проведения программы, tдо	После проведения программы, tпосле	Разность (tдоtпосле)	Абсолютное значение разности	Ранг
1	Г7	9.5	12	-2.5	2.5	17
2	С6	8.5	11	-2.5	2.5	17
3	А6	9.5	10	-0.5	0.5	6,5
4	М7	13	15	-2	2	14
5	К7	8.5	8.5	0	0	3
6	Г6	4.5	8	-3.5	3.5	20
7	Т6	9	11	-2	2	14
8	Л6	12	14	-2	2	14
9	СП6	10	13	-3	3	14
10	Д6	8.5	8.5	0	0	3
11	Д7	9	10	-1	1	8,5
12	А7	7.5	9	-1.5	1.5	11
13	М6	8	7	1	1	8,5
14	С7	10.5	13	-2.5	2.5	17
15	Т6	8	8	0	0	3
16	К6	8	7.5	0.5	0.5	6,5
17	Е6	9	10.5	-1.5	1.5	11
18	Р7	5.5	5.5	0	0	3
19	КС6	8.5	8.5	0	0	3
20	И6	7.5	9	-1.5	1.5	11
Сумма рангов						210

---

Сумма по столбцу рангов равна ∑=210 Проверка правильности составления матрицы на основе исчисления контрольной суммы: Сумма по столбцу и контрольная сумма равны между собой, значит, ранжирование проведено правильно. Теперь отметим те направления, которые являются нетипичными, в данном случае – отрицательными. В Таблице эти направления и соответствующие им ранги выделены цветом. Сумма рангов этих «редких» направлений составляет эмпирическое значение критерия Т: Tэмп=∑Rt=8.5+6.5=15 По таблице значений находим критические значения для Т-критерия Вилкоксона для n=20: Tкр=43 (p≤0.01) Tкр=60 (p≤0.05) Зона значимости в данном случае простирается влево, действительно, если бы "редких", в данном случае положительных, направлений не было совсем, то и сумма их рангов равнялась бы нулю. В данном же случае эмпирическое значение Т попадает в зону значимости: Тэмп<Ткр(0,01). Гипотеза H1 принимается. Показатели «после» проведения программы превышают значения показателей «до».

---