Файл: Оглавление Введение Основные понятия и определения тмм.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 146
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,min/2.
С другой стороны из урав-нений п.5.6.:
ωmax,min=ωс·(1+(-)δ/2).
Таким образом, найдя Ψmax и Ψmin и проведя касательные к диаграмме энергомасс под этими углами к горизонтали (рис.30), получим в точке их пересечения начало новой системы координат
Рис. 30 с осями Т и J1пр, отстоящими от
старых осей на искомую величину Jм и Т0пр.
В целом последовательность определения Jм включает следующие операции:
5.8. Регулирование непериодических колебаний скорости движения машин
В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.
Из уравнения движения машины следует, что изменения скорости рабочего органа можно достигнуть за счет изменения разности работ движущих сил и сил сопротивления (Ад-Ас). Устройства, обеспечивающие изменения работы сил сопротивления применяются в виде тормозов, например, в транспортных машинах, которые снабжаются также и приспособлениями для одновременного разобщения двигателя с машиной – орудием.
Другим способом регулирования является изменение работы движущих сил путем воздействия на орган, подающий энергию к входному звену (поршню у двигателя внутреннего сгорания, лопаткам турбины и т.д.).
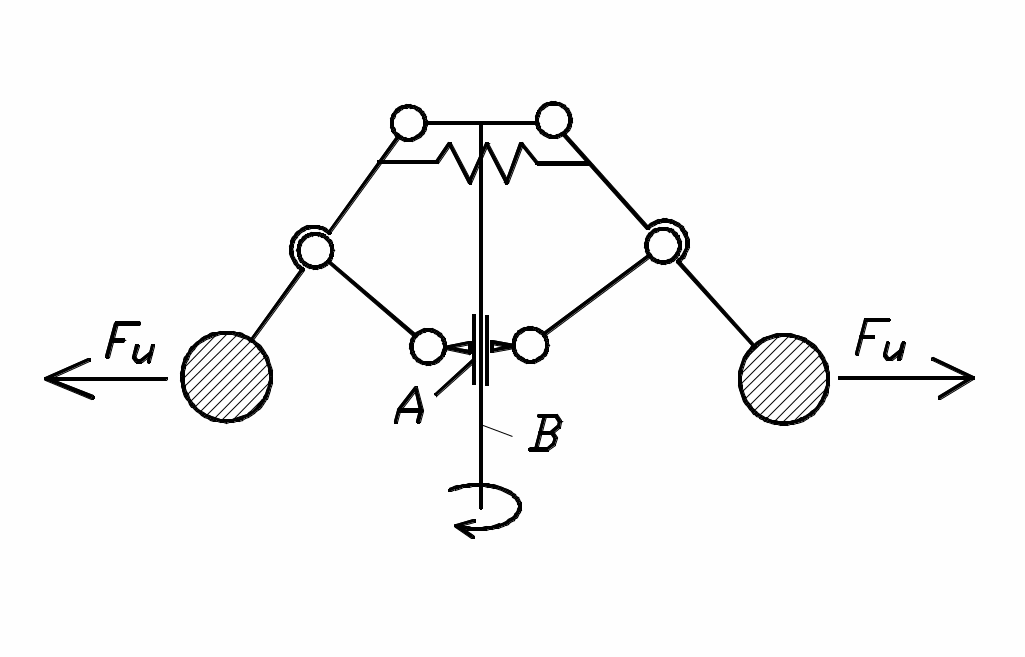
Рис. 31
Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств, называемых регуляторами.
Одним из них является центробежный регулятор (рис.31), приводимый во вращение валом двигателя В. Ползун А соединяется с органом
, подводящим рабочее тело (пар, горючая смесь и т.д.). Регулятор автоматически поддерживает скорость вала двигателя постоянной, т.к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.
5.9. Силовой расчет рычажных механизмов
Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т.е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению.
При кинетостатическом расчете реакции в кинематических парах определяются путем статического расчета, который базируется на результатах кинематического анализа, включая ускорения, необходимые для определения сил (моментов) инерции.
При силовом расчете используется принцип Даламбера, позволяющий решение задачи динамики свести к статическому расчету. Согласно этому принципу приведение ускоренно движущейся системы в равновесие обеспечивается условным приложением к этой системе сил инерции. При этом неизвестные силы определяются из уравнений статики.
Силы взаимодействия между звеньями (реакции) можно считать направлеными по нор-
мали к контактирующим
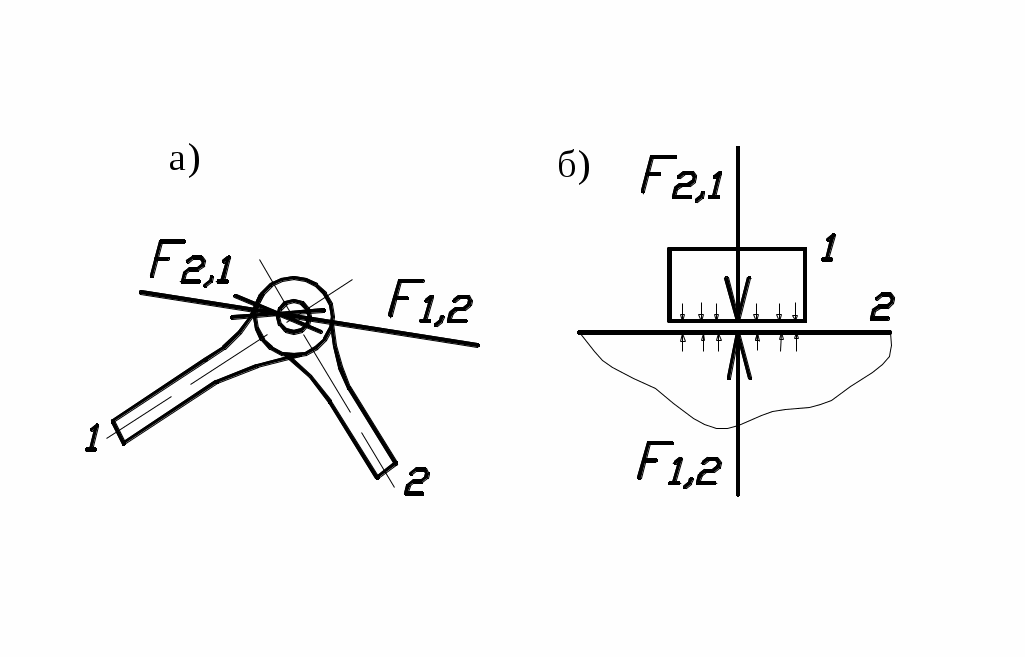
поверхностям, если расчет ведется без учета сил трения (рис.32, а, б).
рис. 32
При графоаналитическом решении используется метод плана сил. Механизм расчленяется на структурные группы Ассура и начальные звенья. Расчет ведется, начиная с последней структурной группы и заканчивается расчетом входного звена.
При расчете структурных групп к ним прикладываются все действующие силы, включая силы инерции и реакции отброшенных связей. Каждая из неиз-
вестных реакций, при необходимости, может быть разложена на две составляющие по выбранным направлениям, например, вдоль оси звена (нормальная Fn) и перпендикулярно оси (тангенциальная Ft). При равенстве числа уравнений статики числу неизвестных реакций их можно определить аналитически и графически, построив многоугольник (план) сил. Неизвестные определятся из условия замкнутости векторной суммы сил. Рассмотрим примеры:
Fi,1t определяется из уравнения моментов для звена 1 - ∑МB=0 относительно т. В. (рис.33, а);
Fj,2t определяется из уравнения моментов для звена 2 - ∑МВ=0 относительно т. В (рис.33,а).
При отрицательных значениях реакций необходимо изменить их направления на противоположные.
Fi,1n и Fj,2n определяются из плана сил (рис.33,б), полученного на основе векторного уравнения;
∑Fk=0, где Fk – силы, действующие на структурную группу.
Рис. 34
Fj,2 определяется из уравнения моментов - ∑МА=0 относительно т. А. Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.34,б) на основе векторного уравнения ∑Fk=0.
Fj,2 определяется из уравнения моментов - ∑МА=0.
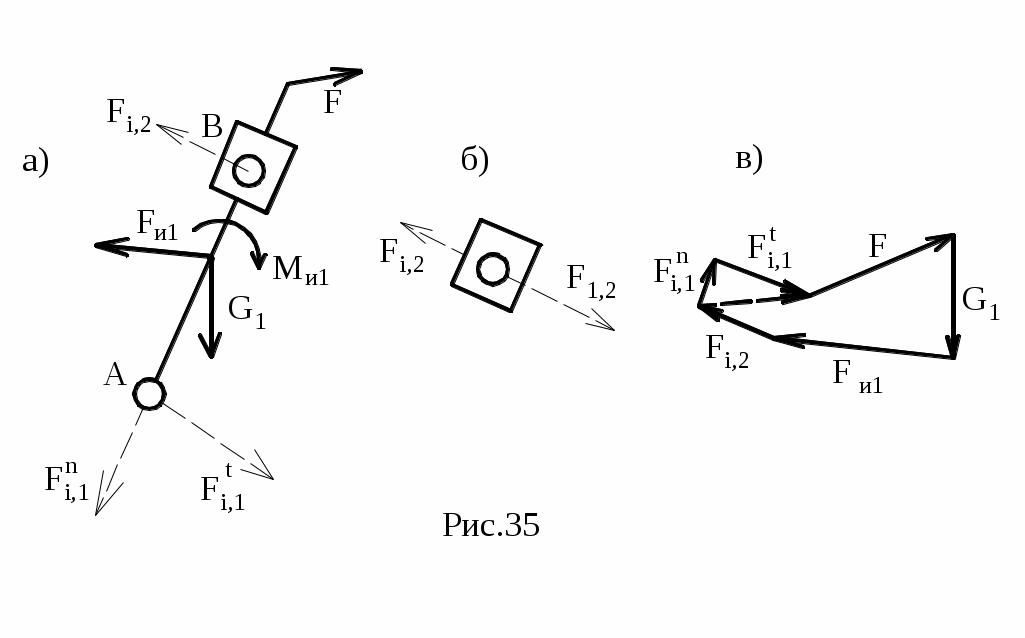
Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.35, в), на основе векторного уравнения ∑Fk=0. При этом особенность расчета данной группы Ассура состоит в возможности некоторого упрощения вычислений в случае, когда весом камня 2 можно пренебречь. Тогда реакция Fj,2 противоположна реакции F1,2 и перпендикулярна АВ, т.е. линия ее действия известна (рис.35, б).
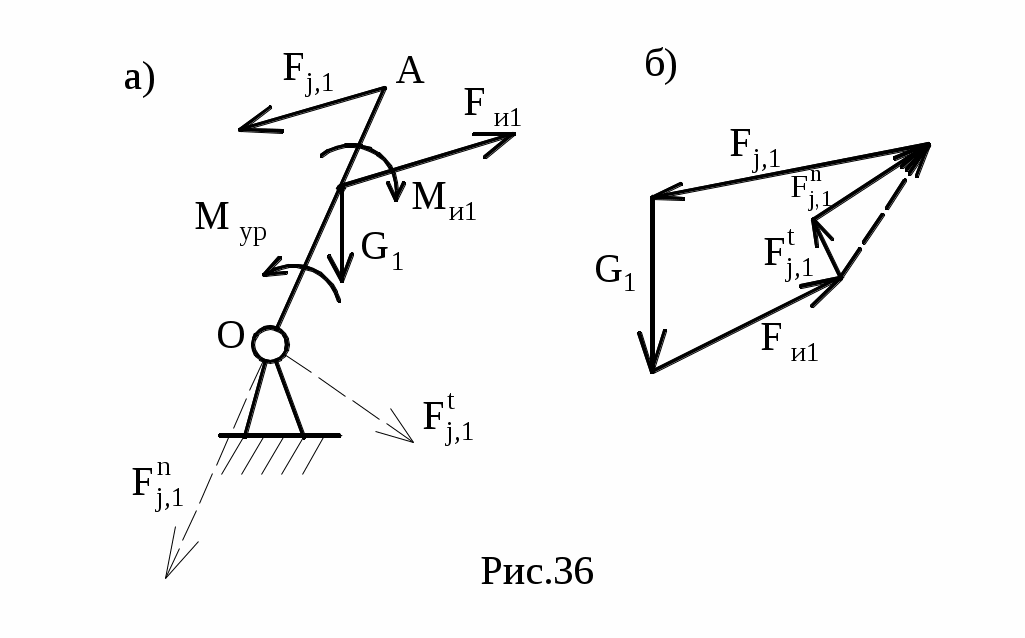
Мур определяется из уравнения моментов - ∑Мо=0.
Fj,1=Fj,1n+Fj,1t определяется из плана сил (рис.36,б) согласно векторному уравнению ∑Fk=0.
6. Синтез рычажных механизмов
6.1. Постановка задачи, виды и способы синтеза
Задачи синтеза рычажных механизмов в общем случае являются сложными задачами оптимального проектирования, включающими этапы структурного, кинематического и динамического расчёта. Поэтому для упрощения решения рассматриваются частные задачи, в которых учитываются лишь некоторые (основные) условия проектирования.
В зависимости от исходных данных различают следующие виды синтеза:
- геометрический, когда заданы отдельные положения звеньев или траектории отдельных точек;
- кинематический, когда заданы некоторые скорости, ускорения или их соотношения;
- динамический, когда заданы действующие силы или наложены некоторые ограничения на динамические параметры.
К способам синтеза относятся:
а) опытный, когда экспериментальным путём подбираются размеры звеньев для реализации заданной траектории;
б) графический;
в) аналитический.
Возможны различные комбинации видов и способов синтеза, перечисленных выше.
6.2. Решение задач оптимального синтеза стержневых механизмов
При постановке задачи оптимального синтеза следует различать входные и выходные параметры.
Входные – это изначально заданные параметры (размеры звеньев, скорости, ускорения или их соотношения).
Выходные – это параметры, определяемые в результате решения задачи.
При синтезе необходимо учитывать ряд требований кинематического, конструктивного, технологического характера и т. д., среди которых одно, как правило, является главным, а остальные – второстепенными (дополнительными). Если главное требование записать математически в виде функции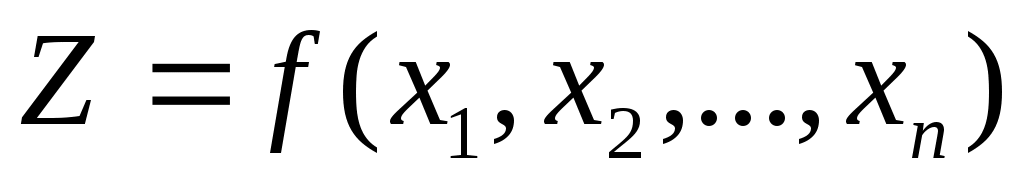
, где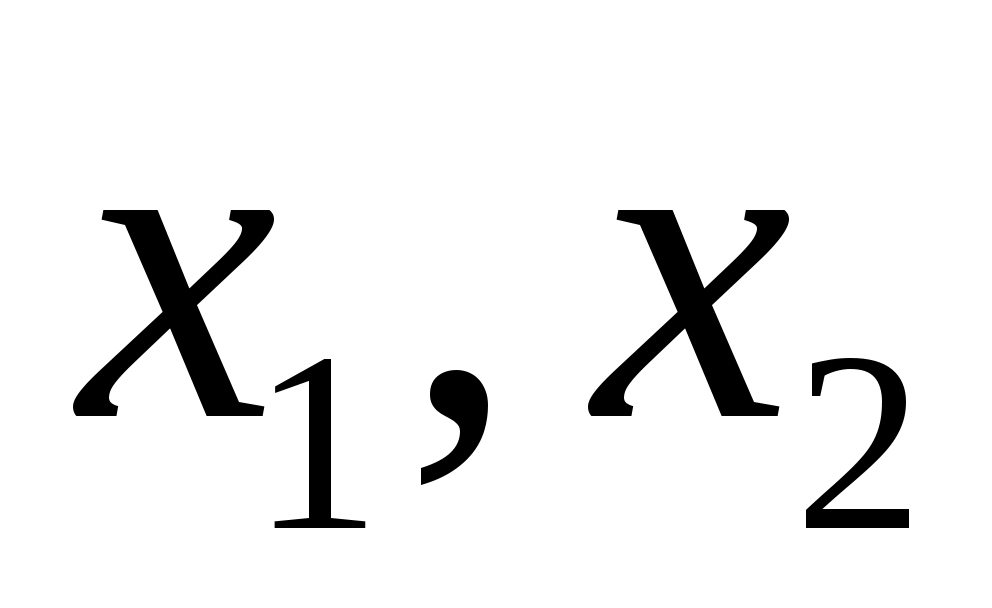 
- выходные параметры, то такая функция называется функцией цели (целевой), при этом дополнительные условия, выраженные в виде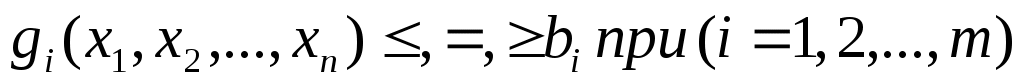 
, называются ограничениями.
Задачей оптимального синтеза является обеспечение экстремального значения Z при соблюдении всех ограничений.
Например, выразив вес механизма в виде функции Z его параметров (длин звеньев) можно решать задачу минимизации Z при соблюдении условий его существования. К таким условиям относятся условия проворачивания кривошипа в шарнирном четырёхзвеннике, условие соблюдения заданного угла давления и ряд других.
При малом числе выходных параметров решение задачи оптимизации может быть получено в аналитической форме. В противном случае используются численные методы направленного, случайного или комбинированного поиска оптимальных решений.
6.3. Условия проворачиваемости кривошипа в шарнирном
четырёхзвеннике
П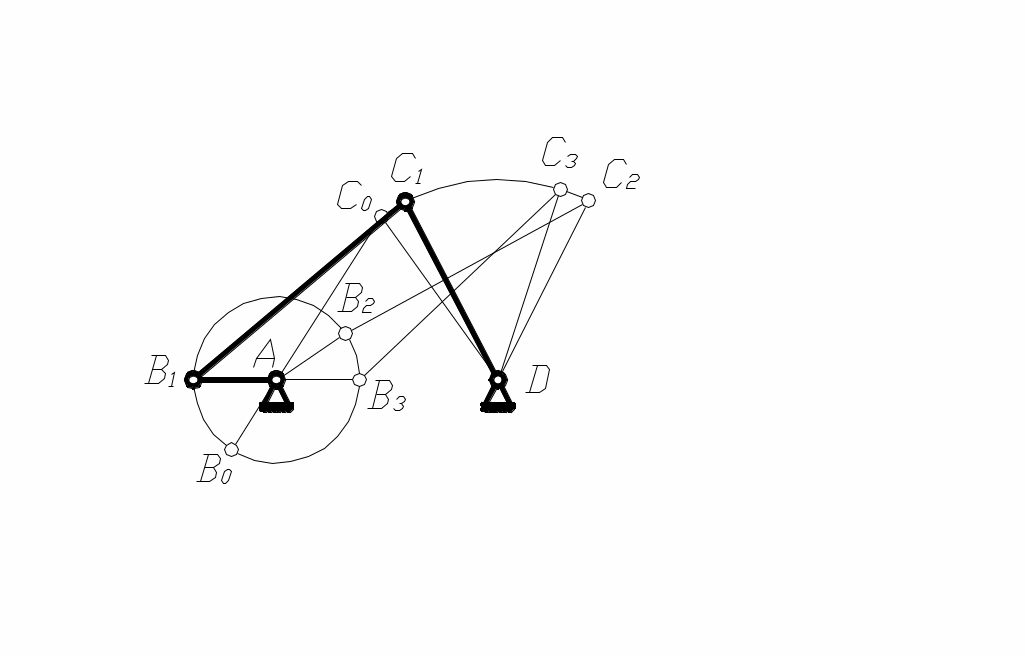
ри проектировании (синтезе) четырёхшарнирного механизма одним из учитываемых условий может быть проворачиваемость звеньев, то есть наличие одного или двух кривошипов. Это зависит от соотношения длин звеньев. Например, для того, чтобы звено АВ четырёхзвенника (рис. 37) могло стать кривошипом, оно должно последовательно пройти через два крайних положения. Используя три положения механизма, получим следующие условия:
для положений 1, 2, 3, предварительно обозначив длины звеньев: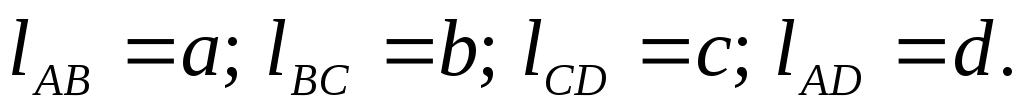
При этом:
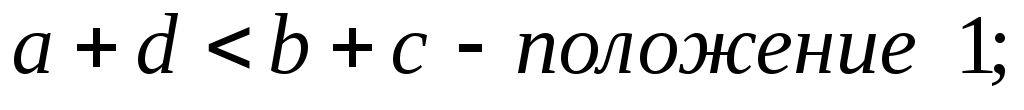
рис.37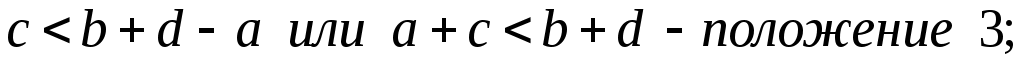
то есть сумма длин кривошипа и любого другого звена меньше суммы остальных звеньев.
Сложим попарно полученные неравенства и получим:
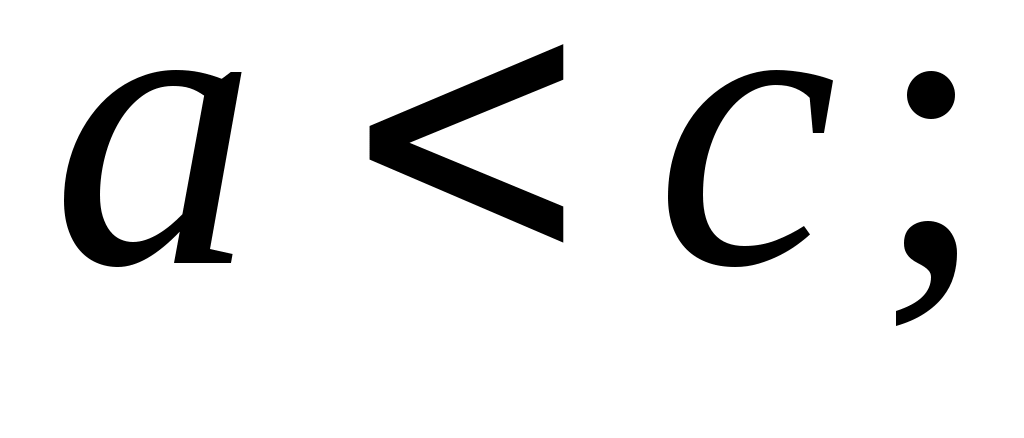
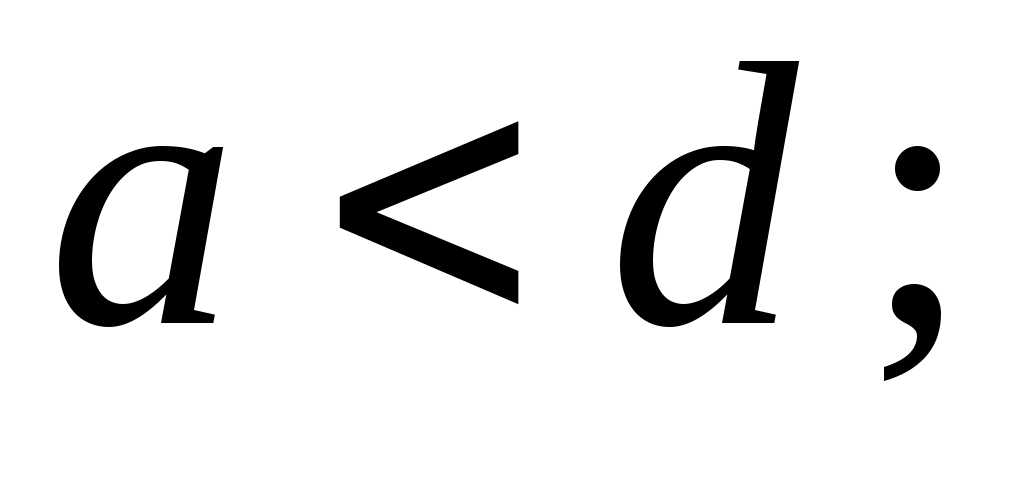
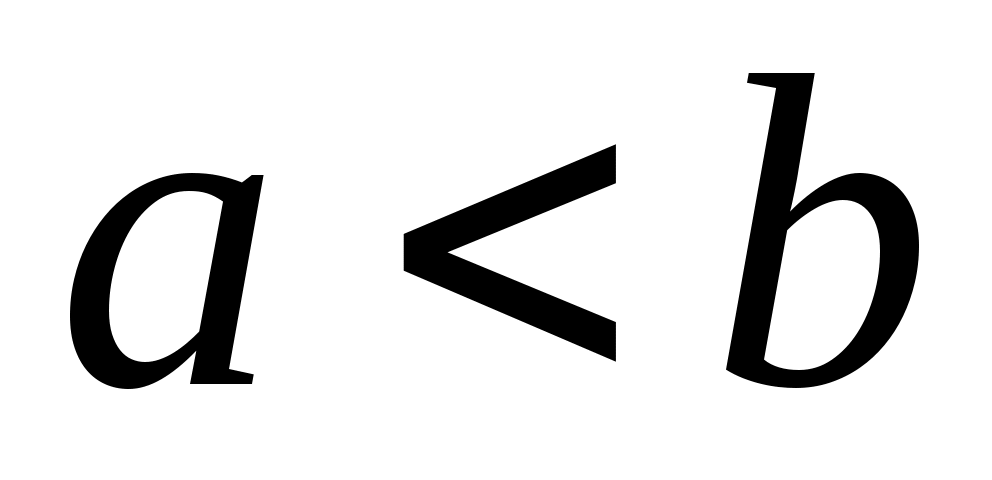, то есть кривошип является самым коротким звеном. А если данные условия не выполняются, то механизм будет либо двухкривошипным, либо двухкоромысловым. Эти условия используются при геометрическом синтезе.
6.4. Учёт углов давления в стержневых механизмах
С другой стороны из урав-нений п.5.6.:
ωmax,min=ωс·(1+(-)δ/2).
Таким образом, найдя Ψmax и Ψmin и проведя касательные к диаграмме энергомасс под этими углами к горизонтали (рис.30), получим в точке их пересечения начало новой системы координат
Рис. 30 с осями Т и J1пр, отстоящими от
старых осей на искомую величину Jм и Т0пр.
В целом последовательность определения Jм включает следующие операции:
-
Строится диаграмма Мпр(φ) для установившегося движения. -
Строится диаграмма ∆Тпр(φ) путем графического интегрирования диаграммы Мпр(φ). -
Строится график Jпр(φ) и диаграмма энергомасс путем исключения параметра φ из графиков ∆Тпр(φ) и Jпр(φ). -
Определяются углы Ψmax и Ψmin, после чего находится Jм в новых координатах Тпр и J1пр диаграммы Тпр(J1пр).
5.8. Регулирование непериодических колебаний скорости движения машин
В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.
Из уравнения движения машины следует, что изменения скорости рабочего органа можно достигнуть за счет изменения разности работ движущих сил и сил сопротивления (Ад-Ас). Устройства, обеспечивающие изменения работы сил сопротивления применяются в виде тормозов, например, в транспортных машинах, которые снабжаются также и приспособлениями для одновременного разобщения двигателя с машиной – орудием.
Другим способом регулирования является изменение работы движущих сил путем воздействия на орган, подающий энергию к входному звену (поршню у двигателя внутреннего сгорания, лопаткам турбины и т.д.).
Рис. 31
Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств, называемых регуляторами.
Одним из них является центробежный регулятор (рис.31), приводимый во вращение валом двигателя В. Ползун А соединяется с органом
, подводящим рабочее тело (пар, горючая смесь и т.д.). Регулятор автоматически поддерживает скорость вала двигателя постоянной, т.к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.
5.9. Силовой расчет рычажных механизмов
Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т.е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению.
При кинетостатическом расчете реакции в кинематических парах определяются путем статического расчета, который базируется на результатах кинематического анализа, включая ускорения, необходимые для определения сил (моментов) инерции.
При силовом расчете используется принцип Даламбера, позволяющий решение задачи динамики свести к статическому расчету. Согласно этому принципу приведение ускоренно движущейся системы в равновесие обеспечивается условным приложением к этой системе сил инерции. При этом неизвестные силы определяются из уравнений статики.
Силы взаимодействия между звеньями (реакции) можно считать направлеными по нор-мали к контактирующим
поверхностям, если расчет ведется без учета сил трения (рис.32, а, б).
рис. 32
При графоаналитическом решении используется метод плана сил. Механизм расчленяется на структурные группы Ассура и начальные звенья. Расчет ведется, начиная с последней структурной группы и заканчивается расчетом входного звена.
При расчете структурных групп к ним прикладываются все действующие силы, включая силы инерции и реакции отброшенных связей. Каждая из неиз-
вестных реакций, при необходимости, может быть разложена на две составляющие по выбранным направлениям, например, вдоль оси звена (нормальная Fn) и перпендикулярно оси (тангенциальная Ft). При равенстве числа уравнений статики числу неизвестных реакций их можно определить аналитически и графически, построив многоугольник (план) сил. Неизвестные определятся из условия замкнутости векторной суммы сил. Рассмотрим примеры:
-
Д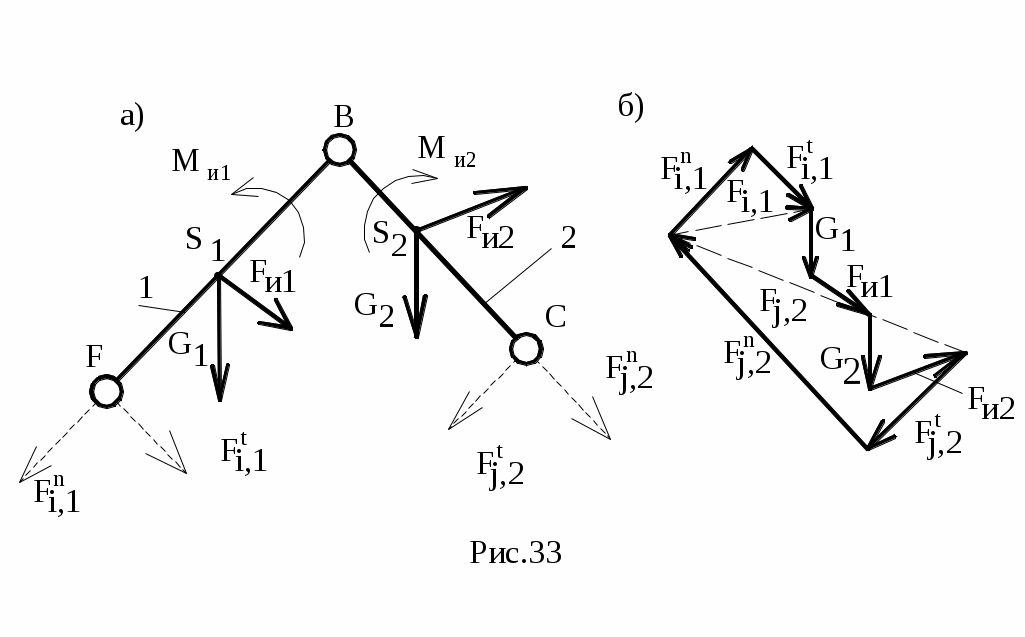
вухповодковая группа с вращательными парами:
Fi,1t определяется из уравнения моментов для звена 1 - ∑МB=0 относительно т. В. (рис.33, а);
Fj,2t определяется из уравнения моментов для звена 2 - ∑МВ=0 относительно т. В (рис.33,а).
При отрицательных значениях реакций необходимо изменить их направления на противоположные.
Fi,1n и Fj,2n определяются из плана сил (рис.33,б), полученного на основе векторного уравнения;
∑Fk=0, где Fk – силы, действующие на структурную группу.
-
Д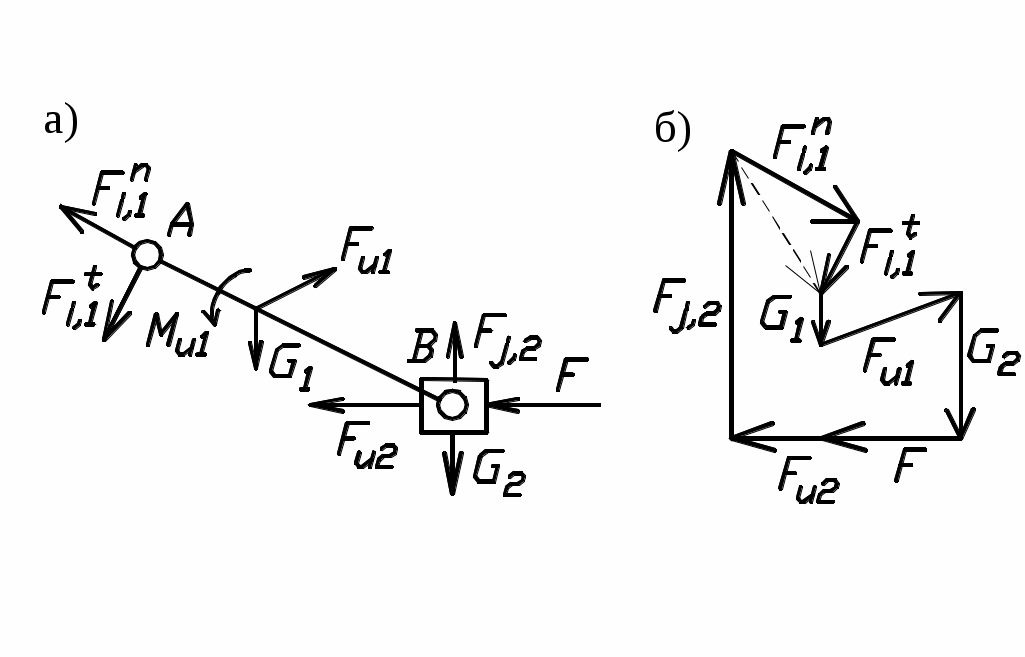
вухповодковая группа шатун-ползун (рис.34, а, б)
Рис. 34
Fj,2 определяется из уравнения моментов - ∑МА=0 относительно т. А. Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.34,б) на основе векторного уравнения ∑Fk=0.
-
Двухповодковая группа кулиса-камень (рис.35, а)
Fj,2 определяется из уравнения моментов - ∑МА=0.
Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.35, в), на основе векторного уравнения ∑Fk=0. При этом особенность расчета данной группы Ассура состоит в возможности некоторого упрощения вычислений в случае, когда весом камня 2 можно пренебречь. Тогда реакция Fj,2 противоположна реакции F1,2 и перпендикулярна АВ, т.е. линия ее действия известна (рис.35, б).
-
Входное (начальное) звено (рис.36, а).
Мур определяется из уравнения моментов - ∑Мо=0.
Fj,1=Fj,1n+Fj,1t определяется из плана сил (рис.36,б) согласно векторному уравнению ∑Fk=0.
6. Синтез рычажных механизмов
6.1. Постановка задачи, виды и способы синтеза
Задачи синтеза рычажных механизмов в общем случае являются сложными задачами оптимального проектирования, включающими этапы структурного, кинематического и динамического расчёта. Поэтому для упрощения решения рассматриваются частные задачи, в которых учитываются лишь некоторые (основные) условия проектирования.
В зависимости от исходных данных различают следующие виды синтеза:
- геометрический, когда заданы отдельные положения звеньев или траектории отдельных точек;
- кинематический, когда заданы некоторые скорости, ускорения или их соотношения;
- динамический, когда заданы действующие силы или наложены некоторые ограничения на динамические параметры.
К способам синтеза относятся:
а) опытный, когда экспериментальным путём подбираются размеры звеньев для реализации заданной траектории;
б) графический;
в) аналитический.
Возможны различные комбинации видов и способов синтеза, перечисленных выше.
6.2. Решение задач оптимального синтеза стержневых механизмов
При постановке задачи оптимального синтеза следует различать входные и выходные параметры.
Входные – это изначально заданные параметры (размеры звеньев, скорости, ускорения или их соотношения).
Выходные – это параметры, определяемые в результате решения задачи.
При синтезе необходимо учитывать ряд требований кинематического, конструктивного, технологического характера и т. д., среди которых одно, как правило, является главным, а остальные – второстепенными (дополнительными). Если главное требование записать математически в виде функции
, где - выходные параметры, то такая функция называется функцией цели (целевой), при этом дополнительные условия, выраженные в виде
, называются ограничениями.
Задачей оптимального синтеза является обеспечение экстремального значения Z при соблюдении всех ограничений.
Например, выразив вес механизма в виде функции Z его параметров (длин звеньев) можно решать задачу минимизации Z при соблюдении условий его существования. К таким условиям относятся условия проворачивания кривошипа в шарнирном четырёхзвеннике, условие соблюдения заданного угла давления и ряд других.
При малом числе выходных параметров решение задачи оптимизации может быть получено в аналитической форме. В противном случае используются численные методы направленного, случайного или комбинированного поиска оптимальных решений.
6.3. Условия проворачиваемости кривошипа в шарнирном
четырёхзвеннике
П
ри проектировании (синтезе) четырёхшарнирного механизма одним из учитываемых условий может быть проворачиваемость звеньев, то есть наличие одного или двух кривошипов. Это зависит от соотношения длин звеньев. Например, для того, чтобы звено АВ четырёхзвенника (рис. 37) могло стать кривошипом, оно должно последовательно пройти через два крайних положения. Используя три положения механизма, получим следующие условия:для положений 1, 2, 3, предварительно обозначив длины звеньев:
При этом:
рис.37
то есть сумма длин кривошипа и любого другого звена меньше суммы остальных звеньев.
Сложим попарно полученные неравенства и получим:
, то есть кривошип является самым коротким звеном. А если данные условия не выполняются, то механизм будет либо двухкривошипным, либо двухкоромысловым. Эти условия используются при геометрическом синтезе.6.4. Учёт углов давления в стержневых механизмах