ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 274
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
этом надо отметить, что трудно обеспечить постоянство усилителя.
Рассмотренные свойства характерны для приемника прямого усиления, без транспонирования спектра. Теперь обратимся к супергетеродинному приемнику с переносом спектра.
Входная цепь (так называемый преселектор) предварительно отделяет сигнал от сигналов соседних мешающих станций. На преобразователь подаются входной сигнал и гармоническое напряжение от местного генератора, называемого гетеродином. Нелинейный элемент преобразователя оказывается под воздействием бигармонического колебания, составленного из сигнала с частотой ωс и напряжения гетеродина с частотой ωг. Пусть характеристика нелинейного элемента квадратична. Тогда в результате преобразования появятся токи комбинационных частот ωс – ωг и ωс – ωг. С помощью избирательной нагрузки можно выделить напряжение только одной из них, например, разностной, которая называется промежуточной частотой:
ωпр. = |ωс – ωг|.
Для различных устройств существует своя промежуточная частота, например, для радиовещательных диапазонов она стандартизована и равна 465 кГц.
Для приема различных станций необходимо перестраивать входную цепь и цепь определяющую частоту гетеродина, так, чтобы разность между частотами сигнала и гетеродина была равной промежуточной частоте.
Таким образом, в супергетеродинном приемнике благодаря преобразованию частоты задача перестройки в основном отделена от задач усиления и избирательности, которые осуществляются на постоянной промежуточной частоте.
Рассмотрим основные соотношения при нелинейном преобразовании частоты. На вход нелинейного преобразователя НП подается напряжение, равное сумме напряжений сигнала:
x(t) = A(t)cos(ωc t + θ) + Aг(t)cos ωг t
На выходе нелинейного преобразователя при помощи фильтра нужно выделить преобразованный сигнал:
S2(t) = KA(t)cos(ωпр t + θ)
с новой несущей частотой ωпр. = ωс – ωг.
Нелинейный преобразователь представим в виде:
y(t) = L[x(t)] = a0 + a1 x(t) + a2 x2(t) + a3 x3(t) + . .
На преобразователь подаются два колебания, то есть
x(t) = s1(t) + sг(t)и поэтому:
y(t) = a0 + a1(s1 + sг) + a2(s1 + sг)2 + a3(s1 + sг)3 + . . .
В выходном сигнале содержатся как полезные, так и паразитные составляющие. Следует выбрать нелинейный преобразователь с такими коэффициентами а0, а1, а2 . . ., чтобы уменьшить число вредных продуктов преобразования; а от неизменно остающихся, следует избавиться с помощью фильтра.
Ограничимся членами преобразователя не выше второй степени; тогда:
y(t) = a0 + a1 s1 + a1 sг + a2 s12 + a2 sг2 + 2a2 s1 sг
Первые пять слагаемых не содержат полезных продуктов преобразования: они представляют собой постоянную составляющую, первую и вторую гармоники частоты сигнала и частоты гетеродина. Шестое слагаемое:
2a2 s1 sг = 2a2 A(t)cos(ωс t + θ)Аг cosωг t =
= a2 A(t)Aг cos[(ωс – ωг)t + θ] + a2 A(t)Aг cos[(ωс + ωг)t + θ]
содержит полезный продукт преобразования – колебание разностной. Используя в качестве нагрузки нелинейного элемента фильтр, настроенный на промежуточную частоту ωпр. = ωс – ωг, находим:
s2(t) = a2 A(t)Aг cos[(ωс – ωг)t + θ].
Следует отметить, что полезный продукт преобразования обусловлен наличием слагаемого второй степени, а точнее квадратической характеристикой.
6.3 Умножение частоты
При умножении частоты, на вход нелинейного преобразователя подается колебание частоты ω0 , а на выходе должно быть колебание частоты nω0 , где n - любое положительное число, то есть,
если s1(t) = Acos(ω0t + φ), то s2(t) = Bcos(nω0t + ψ).
Временные и спектральные диаграммы s1(t) и s2(t) представлены на рисунке 6.5.
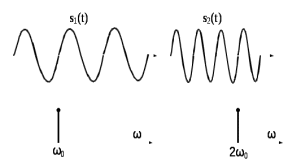
Рис. 6.5 – Умножение частоты в 2 раза
Умножение частоты можно производить или с помощью нелинейных преобразователей, изменяя форму сигнала, или с помощью избирательных систем, выделяющих нужную гармонику из сигнала, содержащую большое число гармоник, например, импульсного сигнала.
Рассмотрим умножитель частоты, основанный на изменении формы гармонического сигнала с помощью нелинейного элемента, аппроксимированного ломаной линией (рисунок 6.3).
Ток n - гармоники определяется коэффициентом Берга αn и максимальным значением ток i :
In = αn(θ)imax.
Для получения наибольшего значения амплитуды нужной гармоники при заданном imax необходимо выбрать θ угол так, чтобы соответствующий коэффициент αn , имел максимальную величину. Оптимальный угол отсечки θопт или рассчитывается по формуле (6.12), или определяется по таблицам [12].
При этом следует учитывать, что коэффициенты имеют хорошо выраженный максимум при:
.
Для удвоения частоты оптимальный угол отчески равен 600.
Известные значения Iмакс и θопт дают возможность по формулам:
Iмакс = SU(1 - cos θ и
определить смещение Е = U0 – Ucosθи амплитуду входного напряжения:
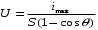, необходимые для обеспечения оптимального режима умножения частоты.
На выходе нелинейного преобразователя образуется множество гармоник, поэтому необходимо включить избирательную цепь, в качестве которой будем использовать LC - колебательный контур.
Как известно, модуль входного сопротивления контура определяется формулой: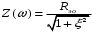
, где Rэо – сопротивление контура на резонансной частоте ω0, а 
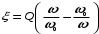, где Q - добротность контура. Уже на частоте второй гармоники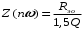 
. Для высоких гармоник величина Z(nω0), примерно, в nQ раз меньше Rэо.
Поскольку максимальные значения коэффициентов Берга быстро убывают с ростом номера гармоники, схемы, использующие рассмотренный метод применяются только для умножения частоты только в два и три раза.
При умножении частоты в более число раз используют последовательность прямоугольных импульсов s(t), представленного рядом Фурье:
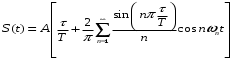
Здесь Т – период повторения импульсов, ωп – частота повторения, τ - длительность импульса. Эта последовательность содержит колебания всех частот, кратных частоте следования импульсов, и может быть использована для умножения частоты. Нужная гармоника выделяется при помощи узкополосного фильтра.
6.4 Контрольные вопросы и задачи
6.4.1 Дайте определение нелинейной цепи и поясните на примере.
6.4.2 На вход двух цепей, аппроксимируемых как L1(x) = a0 + a1xи L2(x) = a0 + a1x + a2x2поступает гармонический сигнал. На выходе каких цепей появятся новые гармоники сигнала, не присутствующих на входе?
6.3.3 Если на вход линейной цепи подается гармонический сигнал, то на выходе он не меняет форму, а изменяется только амплитуда и фаза. Что изменится, если подать гармонический сигнала не вход нелинейной цепи?
6.4.4 Как изменится сигнал на выходе нелинейной цепи, если входной сигнал представить не как s1(t) = Acos(ω0t + φ), аs2(t) = Asin(ω0t + φ)?
6.4.5 На вход нелинейной цепи, представленной как: L2(x) = a0 + a1x + a2x2
подается бигармонический сигнал x(t) = X1cos (ω1t+φ1)+X2cos (ω2t+φ2). Построить спектр сигнала на выходе цепи.
6.4.6 На вход нелинейной цепи, представленной как: L2(x) = a0
+ a1x + a2x2 +а3 х3 подается бигармонический сигнал x(t) = X1cos (ω1t +φ1)+X2cos (ω2t +φ2). Определить количество гармоник сигнала, не присутствующих на входе цепи.
Рассмотренные свойства характерны для приемника прямого усиления, без транспонирования спектра. Теперь обратимся к супергетеродинному приемнику с переносом спектра.
Входная цепь (так называемый преселектор) предварительно отделяет сигнал от сигналов соседних мешающих станций. На преобразователь подаются входной сигнал и гармоническое напряжение от местного генератора, называемого гетеродином. Нелинейный элемент преобразователя оказывается под воздействием бигармонического колебания, составленного из сигнала с частотой ωс и напряжения гетеродина с частотой ωг. Пусть характеристика нелинейного элемента квадратична. Тогда в результате преобразования появятся токи комбинационных частот ωс – ωг и ωс – ωг. С помощью избирательной нагрузки можно выделить напряжение только одной из них, например, разностной, которая называется промежуточной частотой:
ωпр. = |ωс – ωг|.
Для различных устройств существует своя промежуточная частота, например, для радиовещательных диапазонов она стандартизована и равна 465 кГц.
Для приема различных станций необходимо перестраивать входную цепь и цепь определяющую частоту гетеродина, так, чтобы разность между частотами сигнала и гетеродина была равной промежуточной частоте.
Таким образом, в супергетеродинном приемнике благодаря преобразованию частоты задача перестройки в основном отделена от задач усиления и избирательности, которые осуществляются на постоянной промежуточной частоте.
Рассмотрим основные соотношения при нелинейном преобразовании частоты. На вход нелинейного преобразователя НП подается напряжение, равное сумме напряжений сигнала:
x(t) = A(t)cos(ωc t + θ) + Aг(t)cos ωг t
На выходе нелинейного преобразователя при помощи фильтра нужно выделить преобразованный сигнал:
S2(t) = KA(t)cos(ωпр t + θ)
с новой несущей частотой ωпр. = ωс – ωг.
Нелинейный преобразователь представим в виде:
y(t) = L[x(t)] = a0 + a1 x(t) + a2 x2(t) + a3 x3(t) + . .
На преобразователь подаются два колебания, то есть
x(t) = s1(t) + sг(t)и поэтому:
y(t) = a0 + a1(s1 + sг) + a2(s1 + sг)2 + a3(s1 + sг)3 + . . .
В выходном сигнале содержатся как полезные, так и паразитные составляющие. Следует выбрать нелинейный преобразователь с такими коэффициентами а0, а1, а2 . . ., чтобы уменьшить число вредных продуктов преобразования; а от неизменно остающихся, следует избавиться с помощью фильтра.
Ограничимся членами преобразователя не выше второй степени; тогда:
y(t) = a0 + a1 s1 + a1 sг + a2 s12 + a2 sг2 + 2a2 s1 sг
Первые пять слагаемых не содержат полезных продуктов преобразования: они представляют собой постоянную составляющую, первую и вторую гармоники частоты сигнала и частоты гетеродина. Шестое слагаемое:
2a2 s1 sг = 2a2 A(t)cos(ωс t + θ)Аг cosωг t =
= a2 A(t)Aг cos[(ωс – ωг)t + θ] + a2 A(t)Aг cos[(ωс + ωг)t + θ]
содержит полезный продукт преобразования – колебание разностной. Используя в качестве нагрузки нелинейного элемента фильтр, настроенный на промежуточную частоту ωпр. = ωс – ωг, находим:
s2(t) = a2 A(t)Aг cos[(ωс – ωг)t + θ].
Следует отметить, что полезный продукт преобразования обусловлен наличием слагаемого второй степени, а точнее квадратической характеристикой.
6.3 Умножение частоты
При умножении частоты, на вход нелинейного преобразователя подается колебание частоты ω0 , а на выходе должно быть колебание частоты nω0 , где n - любое положительное число, то есть,
если s1(t) = Acos(ω0t + φ), то s2(t) = Bcos(nω0t + ψ).
Временные и спектральные диаграммы s1(t) и s2(t) представлены на рисунке 6.5.
Рис. 6.5 – Умножение частоты в 2 раза
Умножение частоты можно производить или с помощью нелинейных преобразователей, изменяя форму сигнала, или с помощью избирательных систем, выделяющих нужную гармонику из сигнала, содержащую большое число гармоник, например, импульсного сигнала.
Рассмотрим умножитель частоты, основанный на изменении формы гармонического сигнала с помощью нелинейного элемента, аппроксимированного ломаной линией (рисунок 6.3).
Ток n - гармоники определяется коэффициентом Берга αn и максимальным значением ток i :
In = αn(θ)imax.
Для получения наибольшего значения амплитуды нужной гармоники при заданном imax необходимо выбрать θ угол так, чтобы соответствующий коэффициент αn , имел максимальную величину. Оптимальный угол отсечки θопт или рассчитывается по формуле (6.12), или определяется по таблицам [12].
При этом следует учитывать, что коэффициенты имеют хорошо выраженный максимум при:
. Для удвоения частоты оптимальный угол отчески равен 600.
Известные значения Iмакс и θопт дают возможность по формулам:
Iмакс = SU(1 - cos θ и
определить смещение Е = U0 – Ucosθи амплитуду входного напряжения:
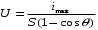, необходимые для обеспечения оптимального режима умножения частоты.На выходе нелинейного преобразователя образуется множество гармоник, поэтому необходимо включить избирательную цепь, в качестве которой будем использовать LC - колебательный контур.
Как известно, модуль входного сопротивления контура определяется формулой:
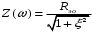, где Rэо – сопротивление контура на резонансной частоте ω0, а 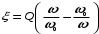, где Q - добротность контура. Уже на частоте второй гармоники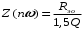
. Для высоких гармоник величина Z(nω0), примерно, в nQ раз меньше Rэо.
Поскольку максимальные значения коэффициентов Берга быстро убывают с ростом номера гармоники, схемы, использующие рассмотренный метод применяются только для умножения частоты только в два и три раза.
При умножении частоты в более число раз используют последовательность прямоугольных импульсов s(t), представленного рядом Фурье:
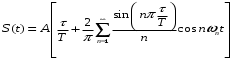
Здесь Т – период повторения импульсов, ωп – частота повторения, τ - длительность импульса. Эта последовательность содержит колебания всех частот, кратных частоте следования импульсов, и может быть использована для умножения частоты. Нужная гармоника выделяется при помощи узкополосного фильтра.
6.4 Контрольные вопросы и задачи
6.4.1 Дайте определение нелинейной цепи и поясните на примере.
6.4.2 На вход двух цепей, аппроксимируемых как L1(x) = a0 + a1xи L2(x) = a0 + a1x + a2x2поступает гармонический сигнал. На выходе каких цепей появятся новые гармоники сигнала, не присутствующих на входе?
6.3.3 Если на вход линейной цепи подается гармонический сигнал, то на выходе он не меняет форму, а изменяется только амплитуда и фаза. Что изменится, если подать гармонический сигнала не вход нелинейной цепи?
6.4.4 Как изменится сигнал на выходе нелинейной цепи, если входной сигнал представить не как s1(t) = Acos(ω0t + φ), аs2(t) = Asin(ω0t + φ)?
6.4.5 На вход нелинейной цепи, представленной как: L2(x) = a0 + a1x + a2x2
подается бигармонический сигнал x(t) = X1cos (ω1t+φ1)+X2cos (ω2t+φ2). Построить спектр сигнала на выходе цепи.
6.4.6 На вход нелинейной цепи, представленной как: L2(x) = a0
+ a1x + a2x2 +а3 х3 подается бигармонический сигнал x(t) = X1cos (ω1t +φ1)+X2cos (ω2t +φ2). Определить количество гармоник сигнала, не присутствующих на входе цепи.