ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 265
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
сигнала условно понимают полосу частот, ограниченную боковыми составляющими, амплитуды которых не превосходят А% от амплитуды максимальной составляющей Uмакс. Обычно А% принимают равным 10%, 5% или 1%.
Следовательно, формула для расчета полосы пропускания представится как:
Δω* = 2рΩ,
где р – порядок бесселевской функции, соответствующей последней боковой, сохранившейся в спектре. Приближенно, полосу частот ЧМ сигнала вычисляют как: Δω* = 2Мчм Ω.
1>
3.3 Фазовая модуляция
Представим несущее колебание (переносчика информации) как высокочастотный сигнал с постоянной амплитудой U0 , частотой ω0 и начальной фазой φ0:
U(t) = U0cos(ω0t+φ0).
При фазовой модуляции необходимо, чтобы по закону низкочастотного колебания изменялась начальная фаза, т.е. нужно получить сигнал вида:
u(t) = U cos[(ω0t+φ(uΩ)]. (3.14)
Здесь φ(uΩ) должна быть линейной функцией напряжения uΩ.
Пусть модулирующий сигнал представляет собой одно гармоническое колебание: тогда закон изменения фазового сдвига запишется как
φ(uΩ) = φ0 +kUΩsinΩt (3.15)
где k - коэффициент пропорциональности, а φ0 - начальная фаза ВЧ колебания.
Введем обозначение
kUΩ = Δφ, (3.16)
где Δφ – максимальное изменение фазы, вызванное низкочастотным модулирующим сигналом. Максимальное изменение фазы называется индексом модуляции и обозначается Мф: Мф = Δφ.
Подставляя (3.15) и (3.16) в (3.14), получаем выражение ФМ колебания:
u(t) = Ucos[(ω0t+ МфsinΩt + φ0],
где φ0 - без потерь общности можно принять равной нулю.
Сравнивая выражения для ЧМ сигнала
и выражение для ФМ сигнала
u(t) = Ucos[(ω0t+ МфsinΩt],
то можно заменить, что они не отличаются друг от друга. Общность структуры выражений объясняется сходством физической природы модулируемых параметров: при фазовой модуляции изменяется фаза колебания, а при частотной – скорость изменения фазы, т.е. её первая производная.
Однако между сигналами ЧМ и ФМ есть существенные различия.
Определим ширину спектра для ЧМ сигнала как:
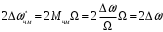
И для ФМ сигнала:
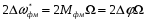
Сравнивая выражения для ЧМ и ФМ сигнала, видно, что при частотной модуляции ширина спектра определяется только девиацией частоты и не зависит от частоты модулирующего сигнала; при фазовой модуляции ширина спектра зависит как от девиации фазы, так и от частоты модулирующего сигнала. Следовательно, ширина спектра для ЧМ сигнала при постоянной амплитуде модулирующего сигнала остается постоянной, а при ФМ ширина спектра изменяется и при изменении частоты модулирующего сигнала. Этот недостаток ФМ не приемлем для системы связи.
3.4 Контрольные вопросы и задачи.
3.4.1 Как определяется глубина модуляции по временной диаграмме АМ
колебаний? Приведите примеры.
3.4.2 Определите глубину модуляции АМ сигналов для модулированного сигнала амплитудой 4 В при модулирующим сигнале амплитудой 2 В.
3.4.3 Построить спектр АМ колебания для модулированного сигнала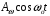
и модулирующих сигналов 
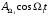и 
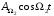где
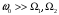и сумма амплитуд модулирующих сигналов не противоречит условию 
.
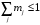3.4.4 Как по спектрограмме АМ колебания определить, присутствует ли перемодуляция АМ колебания, представленного на рисунке 3.6.
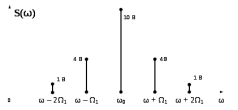
Рис.3.6 – Пример спектра АМ колебания
3.4.5 АМ колебание представлено выражением
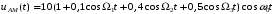, определить его спектральный состав.
3.4.6 Рассчитать среднюю мощность АМ колебания, если мощность несущего сигнала равна 10 Вт, а глубина модуляции равна 0,5.
4.4.7 Определить мощность АМ колебания, промодулированного одним тоном, если мощность несущего сигнала равна 100 Вт, а Ωt = 0, π/2, π, а глубина модуляции равна 0,5.
4.4.8 Определить ширину спектра ЧМ колебания, заданного выражением
S(t) = 10cos(105t + 5cos103t).
4.4.9 Построить спектр для ЧМ колебания для сигнала
S(t) = 10cos(105t + 10cos103t).
4.4.10 Определить ширину спектра ЧМ колебания, заданного выражением
S(t) = 10cos(105t + 0,5cos103t).
4.4.11Дайте развернутый сравнительный анализ ЧМ и ФМ колебаний и перспективы их использования в системе передачи информации.
4.4.12 Задано колебание S(t) = 10cos(105t + 12cos102t). Определить величину девиации частоты.
4 Модулированные дискретные сигналы
4.1. Бинарные сигналы с дискретной модуляцией.
Если сообщение может принимать ряд дискретных значений, то параметры переносчика при модуляции изменяются скачком. Такое скачкообразное изменение параметров называется дискретной модуляцией. На рисунке 4.1 представлены временные характеристики с дискретной амплитудной (ДАМ), частотной (ДЧМ) и фазовой модуляцией (ДФМ) [10].
Рис. 4.1 – Временные зависимости сигналов с дискретной амплитудной, частотной и фазовой модуляцией со скважностью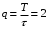
.
Как следует из рисунка 4.1 дискретная модуляция образуется за счет модуляции гармонического переносчика дискретными импульсами с прямоугольной огибающей на интервале от 0 до τ.
Аналитическая запись сигналов ДАМ:
на интервале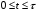
единичный импульс «1» формирует сигнал:
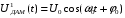
а нулевой символ (пауза) формирует сигнал:
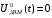
Аналитическая запись сигналов ДЧМ:
на интервале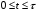 единичный импульс «1» формирует сигнал:
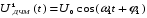(4.1)
а нулевой символ (пауза) формирует сигнал:
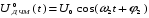(4.2)
Аналитическая запись сигналов ДФМ:
на интервале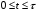 единичный импульс «1» формирует сигнал:
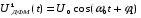(4.3)
а нулевой символ (пауза) формирует сигнал:
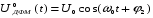(4.4)
Как видно из аналитической записи дискретных модулированных сигналов, свойство ортогональности сигналов ДАМ не вызывает сомнения, так как произведение сигналов, соответствующих разным импульсам равно нулю. Для сигналов ДЧМ, ортогональность достигается или ω1 >> ω2, или ω1 << ω2, или ω1 - ω2 = 1/2τ. Для фазовой модуляции наилучшее значение разности фаз φ1 – φ2 = π, при которой достигается наивысшая помехоустойчивость.
Из-за особенностей построения приемной аппаратуры широко применяется относительная фазовая модуляция (ДОФМ), где информация вносится не в абсолютное значение фазы конкретной посылки, а в разность фаз двух соседних посылок.
При формирование первого сигнала
S1 (t) = U0cos
(ω0t +φ1 )
и второго
S2 (t) = U0cos(ω0t +φ2 )
следует изменить фазу второго сигнала в зависимости от того какой символ передавался «0» или «1», то есть, если надо передать «1», то φ2 = φ1 + π, если надо передать «0» то φ2 = φ1. На приеме необходимо обрабатывать сигналы на двух посылках, чтобы определить какой символ был передан. В упрощенном виде демодулятор определять знак выражения cos(φ2 - φ1 ), то есть если значение отрицательное, то демодулятор принимает решение, что передавался «1», если положительное то «0».
На рисунке 4.2 показаны спектры сигналов с ДАМ, ДФМ и ДЧМ. Они получаются на основе общего правила построения спектров модулированного сигнала по спектру модулирующего НЧ сигнала путем его переноса из «0» на частоту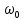
.
Рассмотрим спектральный состав сигналов дискретной модуляции, представленный на рисунке 4.2.
Будем предполагать, что модуляция производится двоичным сообщением, представляющим собой периодическую последовательность прямоугольных импульсов с периодом Т = 2τи [4 ]:
a(t) = 1 если 0 < t < τи и - 1, если - τи < t < 0
Это двоичное сообщение представляем рядом Фурье:
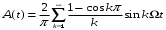(4.5)
Сигнал ДАМ можно записать в виде:
=
=
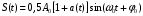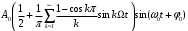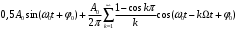+ (4.6)
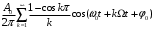
Построенный по этой формуле спектр сигнала ДАМ показан на рисунке 4.2 [5].
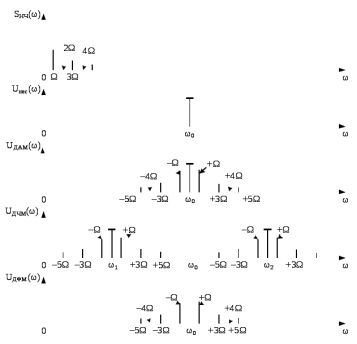
Рис.4.2 – Спектральные характеристики модулирующего сигнала и сигналов с ДАМ, ДЧМ и ДФМ.
Спектр ДЧМ, представленного на рисунке 4.2 можно рассматривать как сумму двух спектров ДАМ с поднесущими ω2 и ω1, где ω2 >> ω1
SДЧМ(ω) = SДАМ(ω1) + SДАМ(ω2)
При передаче реальных дискретных сообщений, чередование посылок (символов «1» и «0») носит случайный характер
Следовательно, формула для расчета полосы пропускания представится как:
Δω* = 2рΩ,
где р – порядок бесселевской функции, соответствующей последней боковой, сохранившейся в спектре. Приближенно, полосу частот ЧМ сигнала вычисляют как: Δω* = 2Мчм Ω.
1>
3.3 Фазовая модуляция
Представим несущее колебание (переносчика информации) как высокочастотный сигнал с постоянной амплитудой U0 , частотой ω0 и начальной фазой φ0:
U(t) = U0cos(ω0t+φ0).
При фазовой модуляции необходимо, чтобы по закону низкочастотного колебания изменялась начальная фаза, т.е. нужно получить сигнал вида:
u(t) = U cos[(ω0t+φ(uΩ)]. (3.14)
Здесь φ(uΩ) должна быть линейной функцией напряжения uΩ.
Пусть модулирующий сигнал представляет собой одно гармоническое колебание: тогда закон изменения фазового сдвига запишется как
φ(uΩ) = φ0 +kUΩsinΩt (3.15)
где k - коэффициент пропорциональности, а φ0 - начальная фаза ВЧ колебания.
Введем обозначение
kUΩ = Δφ, (3.16)
где Δφ – максимальное изменение фазы, вызванное низкочастотным модулирующим сигналом. Максимальное изменение фазы называется индексом модуляции и обозначается Мф: Мф = Δφ.
Подставляя (3.15) и (3.16) в (3.14), получаем выражение ФМ колебания:
u(t) = Ucos[(ω0t+ МфsinΩt + φ0],
где φ0 - без потерь общности можно принять равной нулю.
Сравнивая выражения для ЧМ сигнала
и выражение для ФМ сигнала
u(t) = Ucos[(ω0t+ МфsinΩt],
то можно заменить, что они не отличаются друг от друга. Общность структуры выражений объясняется сходством физической природы модулируемых параметров: при фазовой модуляции изменяется фаза колебания, а при частотной – скорость изменения фазы, т.е. её первая производная.
Однако между сигналами ЧМ и ФМ есть существенные различия.
Определим ширину спектра для ЧМ сигнала как:
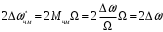
И для ФМ сигнала:
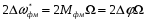
Сравнивая выражения для ЧМ и ФМ сигнала, видно, что при частотной модуляции ширина спектра определяется только девиацией частоты и не зависит от частоты модулирующего сигнала; при фазовой модуляции ширина спектра зависит как от девиации фазы, так и от частоты модулирующего сигнала. Следовательно, ширина спектра для ЧМ сигнала при постоянной амплитуде модулирующего сигнала остается постоянной, а при ФМ ширина спектра изменяется и при изменении частоты модулирующего сигнала. Этот недостаток ФМ не приемлем для системы связи.
3.4 Контрольные вопросы и задачи.
3.4.1 Как определяется глубина модуляции по временной диаграмме АМ
колебаний? Приведите примеры.
3.4.2 Определите глубину модуляции АМ сигналов для модулированного сигнала амплитудой 4 В при модулирующим сигнале амплитудой 2 В.
3.4.3 Построить спектр АМ колебания для модулированного сигнала
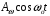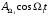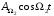и модулирующих сигналов и где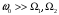 и сумма амплитуд модулирующих сигналов не противоречит условию 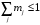. 3.4.4 Как по спектрограмме АМ колебания определить, присутствует ли перемодуляция АМ колебания, представленного на рисунке 3.6.
Рис.3.6 – Пример спектра АМ колебания
3.4.5 АМ колебание представлено выражением
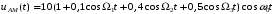, определить его спектральный состав.3.4.6 Рассчитать среднюю мощность АМ колебания, если мощность несущего сигнала равна 10 Вт, а глубина модуляции равна 0,5.
4.4.7 Определить мощность АМ колебания, промодулированного одним тоном, если мощность несущего сигнала равна 100 Вт, а Ωt = 0, π/2, π, а глубина модуляции равна 0,5.
4.4.8 Определить ширину спектра ЧМ колебания, заданного выражением
S(t) = 10cos(105t + 5cos103t).
4.4.9 Построить спектр для ЧМ колебания для сигнала
S(t) = 10cos(105t + 10cos103t).
4.4.10 Определить ширину спектра ЧМ колебания, заданного выражением
S(t) = 10cos(105t + 0,5cos103t).
4.4.11Дайте развернутый сравнительный анализ ЧМ и ФМ колебаний и перспективы их использования в системе передачи информации.
4.4.12 Задано колебание S(t) = 10cos(105t + 12cos102t). Определить величину девиации частоты.
4 Модулированные дискретные сигналы
4.1. Бинарные сигналы с дискретной модуляцией.
Если сообщение может принимать ряд дискретных значений, то параметры переносчика при модуляции изменяются скачком. Такое скачкообразное изменение параметров называется дискретной модуляцией. На рисунке 4.1 представлены временные характеристики с дискретной амплитудной (ДАМ), частотной (ДЧМ) и фазовой модуляцией (ДФМ) [10].
Рис. 4.1 – Временные зависимости сигналов с дискретной амплитудной, частотной и фазовой модуляцией со скважностью
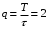.Как следует из рисунка 4.1 дискретная модуляция образуется за счет модуляции гармонического переносчика дискретными импульсами с прямоугольной огибающей на интервале от 0 до τ.
Аналитическая запись сигналов ДАМ:
на интервале
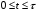единичный импульс «1» формирует сигнал: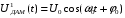 а нулевой символ (пауза) формирует сигнал:
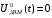
Аналитическая запись сигналов ДЧМ:
на интервале
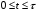единичный импульс «1» формирует сигнал: 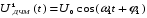(4.1)а нулевой символ (пауза) формирует сигнал:
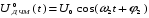(4.2)Аналитическая запись сигналов ДФМ:
на интервале
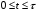единичный импульс «1» формирует сигнал: 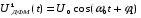(4.3)а нулевой символ (пауза) формирует сигнал:
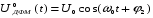(4.4)Как видно из аналитической записи дискретных модулированных сигналов, свойство ортогональности сигналов ДАМ не вызывает сомнения, так как произведение сигналов, соответствующих разным импульсам равно нулю. Для сигналов ДЧМ, ортогональность достигается или ω1 >> ω2, или ω1 << ω2, или ω1 - ω2 = 1/2τ. Для фазовой модуляции наилучшее значение разности фаз φ1 – φ2 = π, при которой достигается наивысшая помехоустойчивость.
Из-за особенностей построения приемной аппаратуры широко применяется относительная фазовая модуляция (ДОФМ), где информация вносится не в абсолютное значение фазы конкретной посылки, а в разность фаз двух соседних посылок.
При формирование первого сигнала
S1 (t) = U0cos
(ω0t +φ1 )
и второго
S2 (t) = U0cos(ω0t +φ2 )
следует изменить фазу второго сигнала в зависимости от того какой символ передавался «0» или «1», то есть, если надо передать «1», то φ2 = φ1 + π, если надо передать «0» то φ2 = φ1. На приеме необходимо обрабатывать сигналы на двух посылках, чтобы определить какой символ был передан. В упрощенном виде демодулятор определять знак выражения cos(φ2 - φ1 ), то есть если значение отрицательное, то демодулятор принимает решение, что передавался «1», если положительное то «0».
На рисунке 4.2 показаны спектры сигналов с ДАМ, ДФМ и ДЧМ. Они получаются на основе общего правила построения спектров модулированного сигнала по спектру модулирующего НЧ сигнала путем его переноса из «0» на частоту
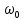.Рассмотрим спектральный состав сигналов дискретной модуляции, представленный на рисунке 4.2.
Будем предполагать, что модуляция производится двоичным сообщением, представляющим собой периодическую последовательность прямоугольных импульсов с периодом Т = 2τи [4 ]:
a(t) = 1 если 0 < t < τи и - 1, если - τи < t < 0
Это двоичное сообщение представляем рядом Фурье:
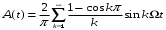(4.5)Сигнал ДАМ можно записать в виде:
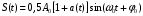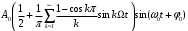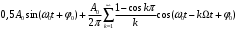= = + (4.6)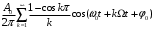 Построенный по этой формуле спектр сигнала ДАМ показан на рисунке 4.2 [5].
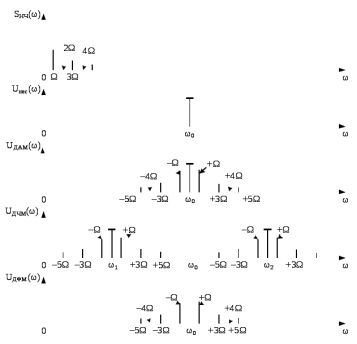
Рис.4.2 – Спектральные характеристики модулирующего сигнала и сигналов с ДАМ, ДЧМ и ДФМ.
Спектр ДЧМ, представленного на рисунке 4.2 можно рассматривать как сумму двух спектров ДАМ с поднесущими ω2 и ω1, где ω2 >> ω1
SДЧМ(ω) = SДАМ(ω1) + SДАМ(ω2)
При передаче реальных дискретных сообщений, чередование посылок (символов «1» и «0») носит случайный характер