Файл: Методические указания и контрольные задания для студентов заочной формы обучения для специальности.doc

Указания к решению задачи 4
В данной задаче необходимо произвести расчет параметров цепи с параллельным соединением двух ветвей.

Расчет можно произвести с помощью векторных диаграмм и ряда формул, многие из которых легко выводятся из векторных диаграмм. При этом расчет электрических цепей переменного тока значительно упрощается и приобретает особую наглядность при использовании векторных диаграмм.

Расчет разветвленной цепи можно производить аналитически с помощью метода проводимостей.

Индексы буквенных обозначений в задачах задания 4 соответствуют индексам сопротивлений соответствующих им ветвей. Например: и - активная мощность сопротивлений первой и второй ветви; и - ток первой и второй ветви соответственно и т.д.

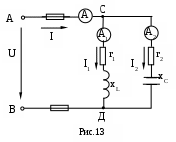
Пример 9. Для электрической цепи переменного тока (рис.13) определить показания амперметров , , , углы сдвига фаз , и между соответствующими токами , и и напряжением , если питающее напряжение , а активные и реактивные сопротивления цепи:

---

; ; ; .

Дано: , ; ; ; .

Определить: , , , , , .

Решение: Определим полное сопротивление ветвей в цепи:

;

.

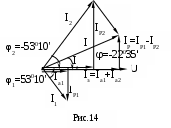
Углы сдвига фаз между токами и напряжениями соответствующих параллельных ветвей:

; ;

; .

Показания амперметров и в параллельных ветвях:

; .

Активные составляющие токов в параллельных ветвях:

---

;

;

; .

Реактивные составляющие токов в параллельных ветвях:

;

.

Активные и реактивные составляющие общего тока:

;

.

Общий ток в цепи: .

Угол сдвига фаз между током и приложенным напряжением :

; .

Ответ: ; ; ; ; ; .



Пример 10. Пример 9 решить методом проводимостей.

Решение: Значения величин полных сопротивлений , , токов , и коэффициентов мощности

---

, определяются методом, изложенным выше (см. пример 9):

; ; ; ; ; .

Активные и реактивные проводимости параллельных ветвей:

;

.

Полная проводимость всей цепи:

.

Общий ток в цепи:

.

Угол сдвига фаз между общим током I и приложенным напряжением U:

; .

Пример 11. Цепь переменного тока состоит из двух ветвей, соединенных параллельно. Первая ветвь содержит катушку с активным и индуктивным сопротивлениями, во вторую ветвь включен конденсатор с емкостным сопротивлением и последовательно с ним активное сопротивление (рис.13). Активная мощность, потребляемая первой ветвью .

Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные и реактивные мощности цепи; 3) напряжение, приложенное к цепи; 4) угол сдвига фаз между током неразветвленной части цепи и напряжением. Начертить в масштабе векторную диаграмму цепи.

Дано:

---

, , , , .

Определить: , , , P, Q, U, φ.

Решение: Активная мощность теряется в активном сопротивлении . Из формулы определим силу тока в первой ветви:

.

Определим напряжение, приложенное к цепи:



Определим силу тока проходящего по второй ветви:

.

Найдем активную и реактивную мощности, потребляемые цепью:





Знак «-» показывает, что преобладает реактивная мощность емкостного характера.

Полная мощность, потребляемая цепью:

.

Определим ток в неразветвленной части цепи:

.

Угол сдвига фаз во всей цепи находим через во избежание потери знака угла:

; .

Знак «-» подчеркивает, что ток цепи опережает напряжение U цепи.

Для построения векторной диаграммы необходимо определить следующие дополнительные величины:

---