ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 162
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
тела относительно оси вращения;
– угловая скорость вращения.
Моментом инерции тела относительно оси z называется скалярная величина:
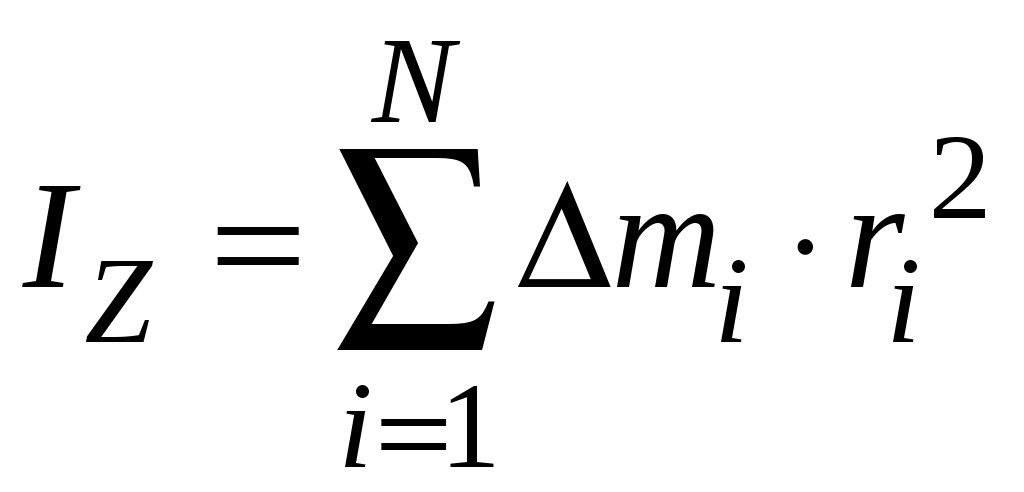 .
.
Здесь считается, что мы мысленно разбили тело на очень большое число N оченьмаленьких кусочков, каждый из которых можно считать материальной точкой, при этом
mi – масса i-го кусочка;
ri – расстояние от i-го кусочка до оси z.
На самом деле, момент инерции тела относительно оси zесть тройной интеграл, вычисляемый по всему объему тела:
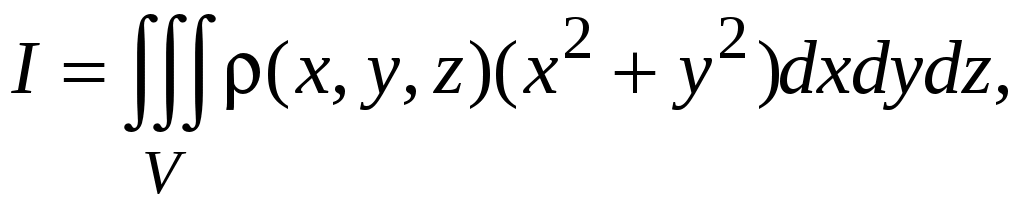
где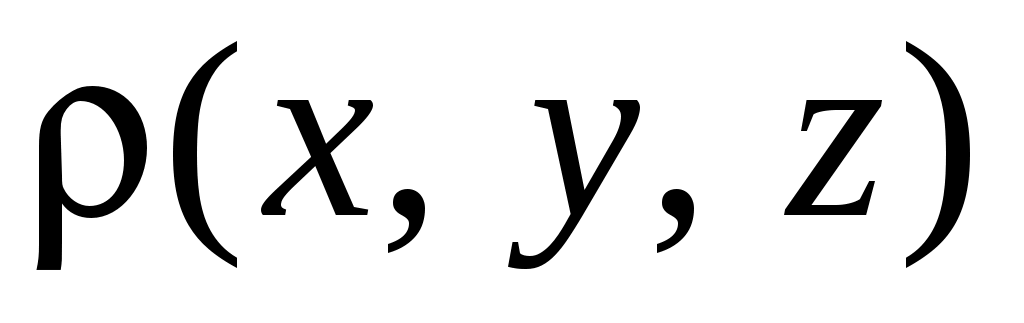 – плотность тела, в общем случае зависящая от декартовых координат x,y,z.
– плотность тела, в общем случае зависящая от декартовых координат x,y,z.
Момент инерции – величина аддитивная, то есть момент инерции системы из N тел относительно оси равен сумме моментов инерции всех тел системы относительно той же оси:
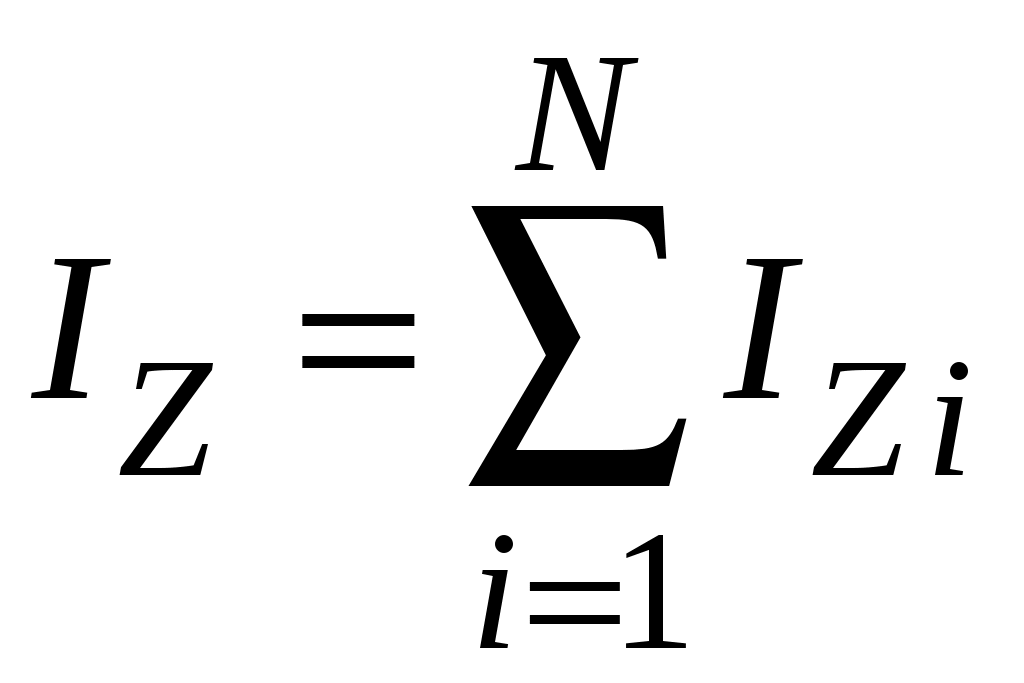 .
.
Момент инерции материальной точки относительно оси z, очевидно, равен:
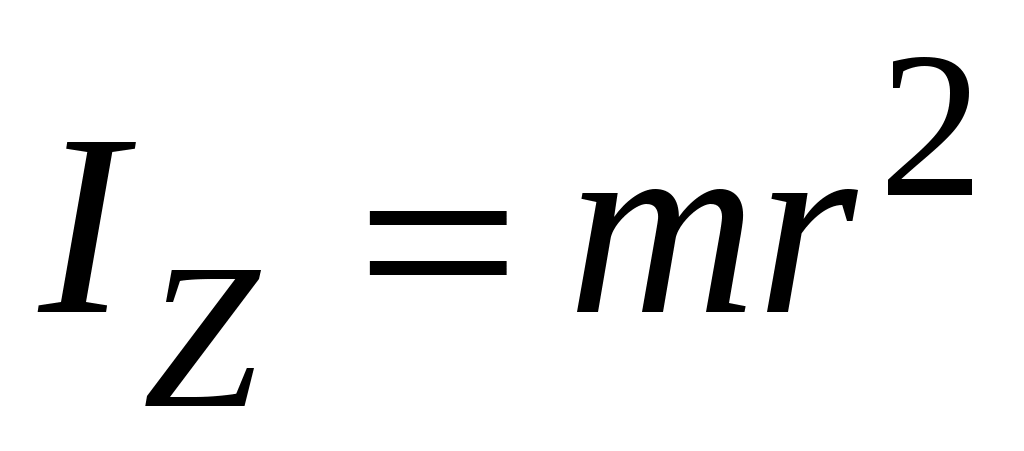 ,
,
где m – масса материальной точки;
r – расстояние от точки до данной оси.
Формулы для вычисления моментов инерции простейших симметричных абсолютно твердых тел приведены в табл. 2.1.
Таблица 2.1
Окончание табл. 2.1
При вычислении моментов инерции часто используется теорема Штейнера:
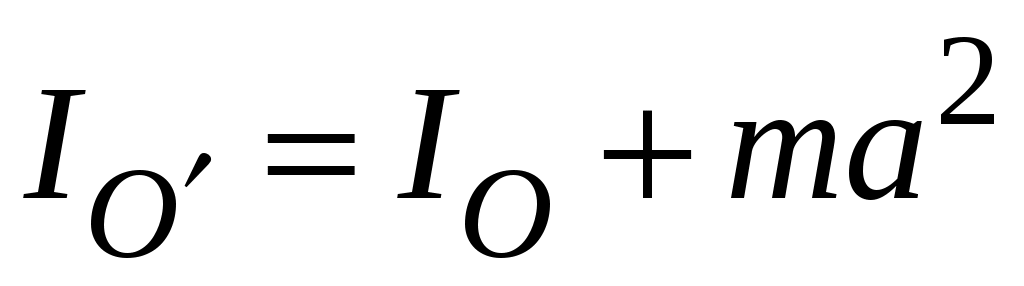 , (2.14)
, (2.14)
где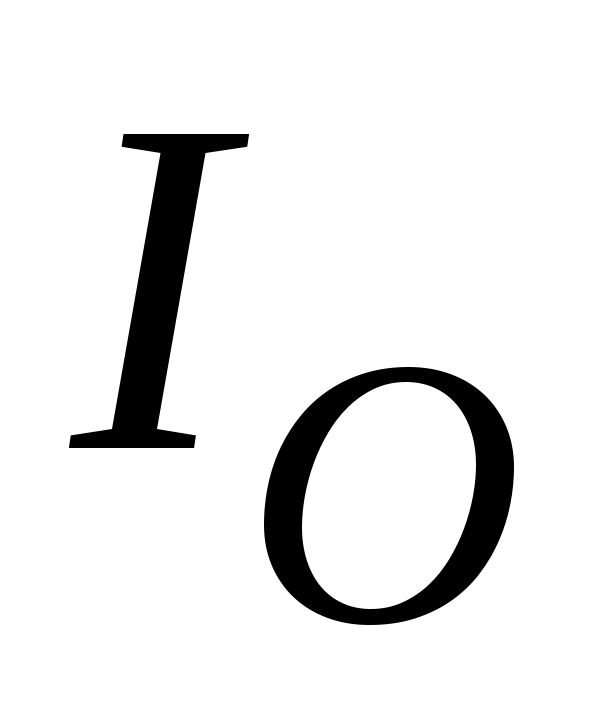 – момент инерции тела относительно оси O, проходящей через центр масс тела;
– момент инерции тела относительно оси O, проходящей через центр масс тела;
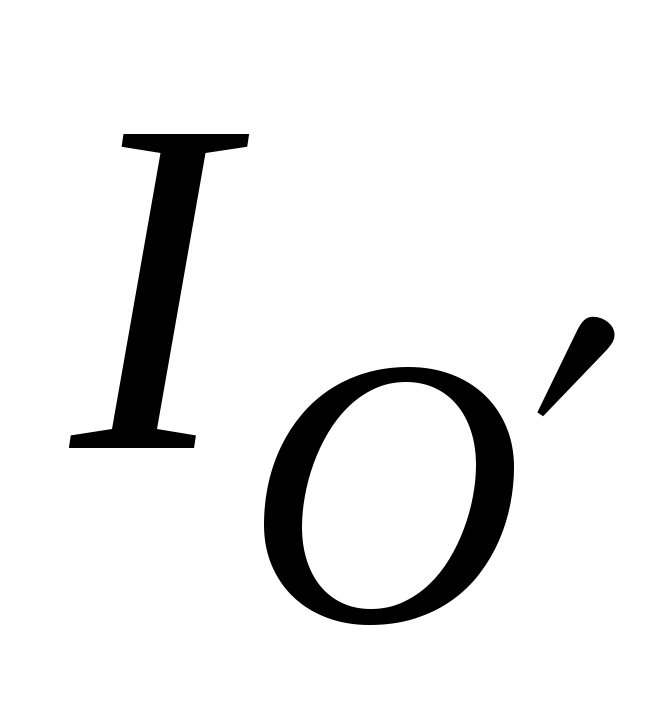 – момент инерции тела относительно параллельной осиO', не проходящей через центр масс;
– момент инерции тела относительно параллельной осиO', не проходящей через центр масс;
m – масса тела;
a – расстояние между осями O иO'.
В случае, если твердое тело вращается вокруг оси z, его момент импульса относительно этой оси можно вычислить по формуле:
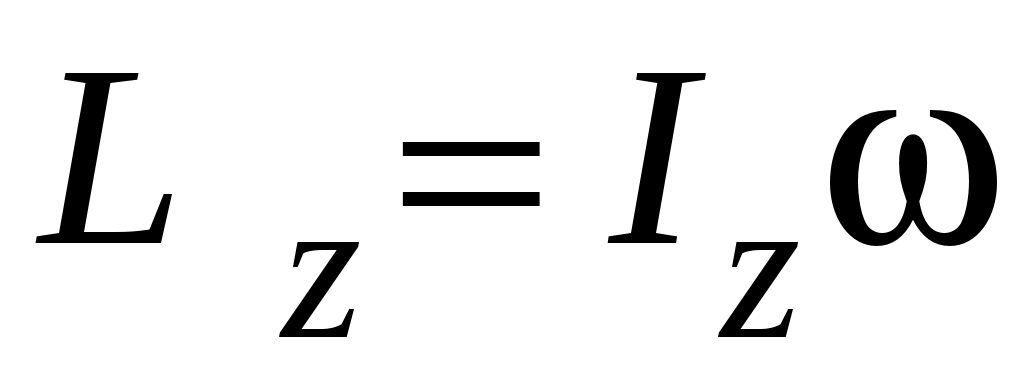 ,
,
где – угловая скорость вращения тела.
– угловая скорость вращения тела.
Можно показать, что при вращении тела вокруг неподвижной оси под действием силы элементарная работа силы определяется скалярным произведением вектора момента силы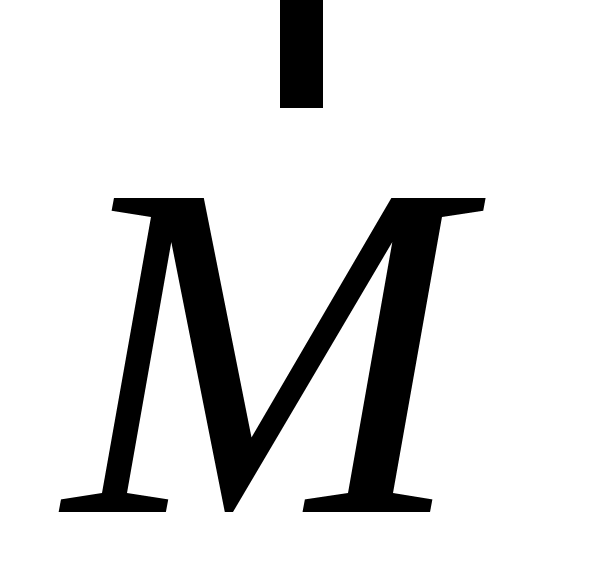 на вектор угла поворота тела
на вектор угла поворота тела 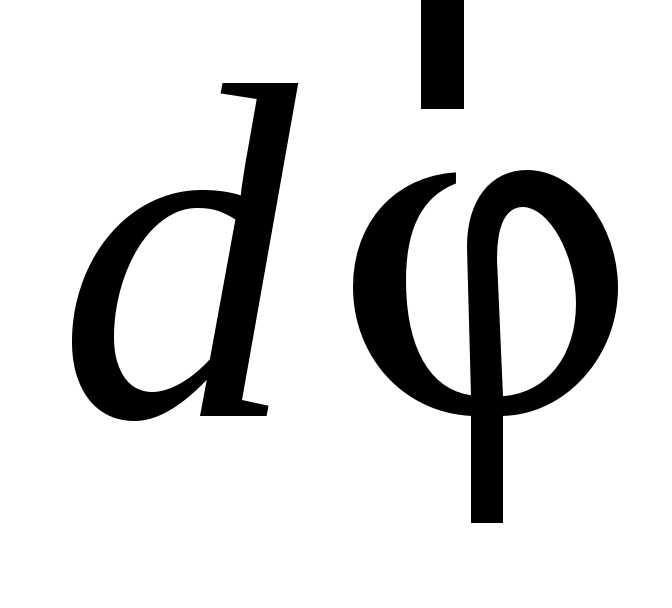 :
:
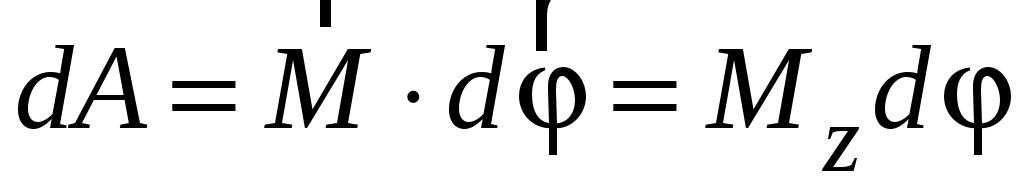 ,
,
где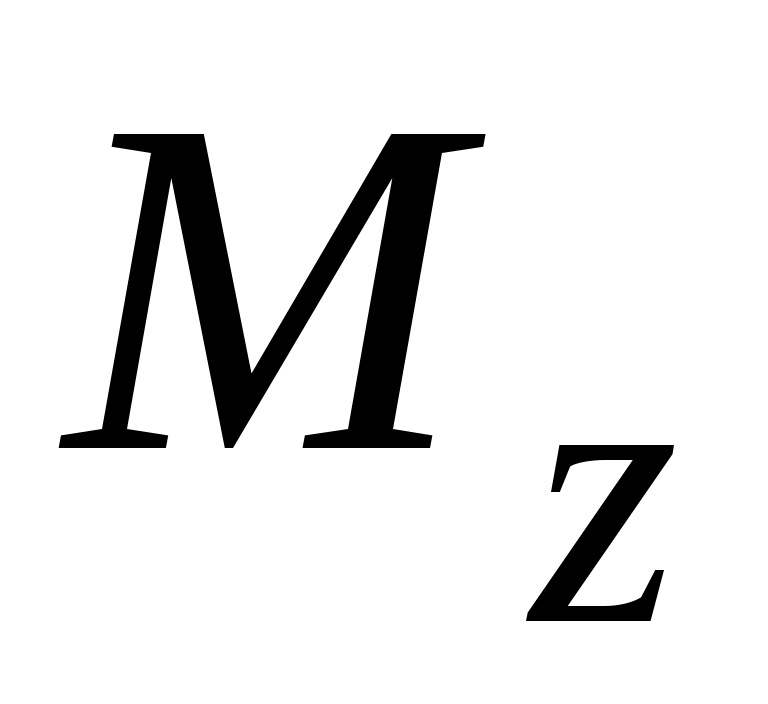
– момент силы относительно оси вращения.
Следовательно, при повороте на конечный угол :
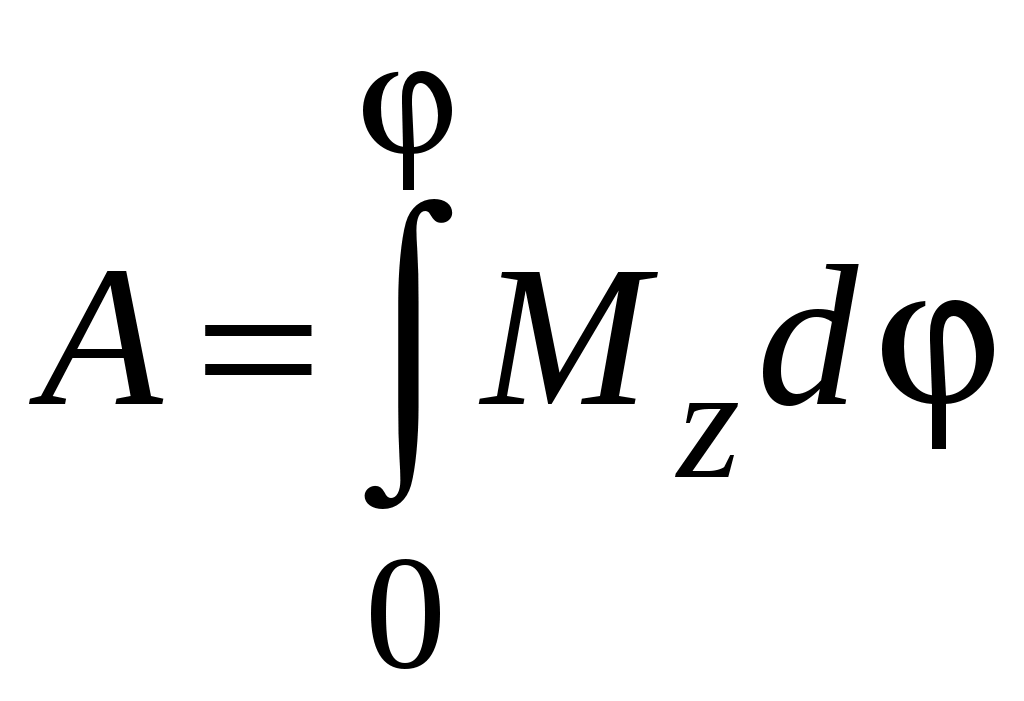 ,
,
а если момент силы постоянен (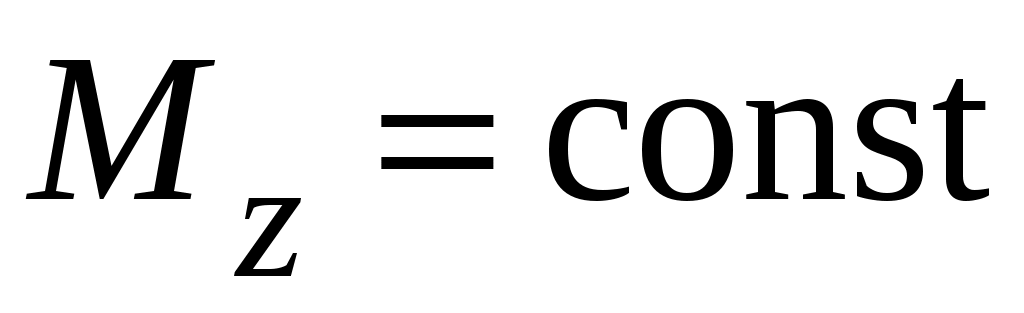 ), то
), то
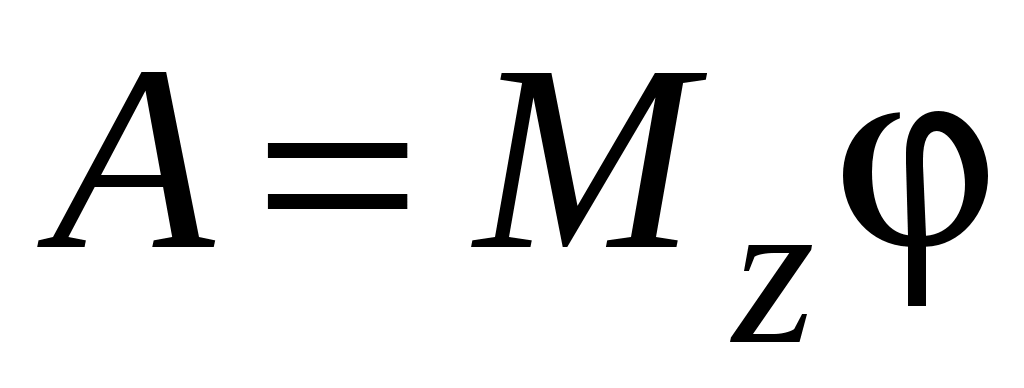 . (2.15)
. (2.15)
Экспериментальная установка и метод измерения
На рис. 2.3 представлен маятник Обербека, состоящий из двух стержней и шкива радиусом R, закрепленных на горизонтальной оси вращения. По стержням могут перемещаться и симметрично закрепляются в нужном положении два (по одному на каждом стержне) груза одинаковой массы.
На шкив наматывается нить, к концу которой крепится платформа с грузом. Примем массу платформы m1, а массу груза m2, в результате общая масса m = m1 + m2.
Если груз m поднять, намотав нить на шкив, на некоторую высоту h1 и отпустить, то груз придет в движение, а сила натяжения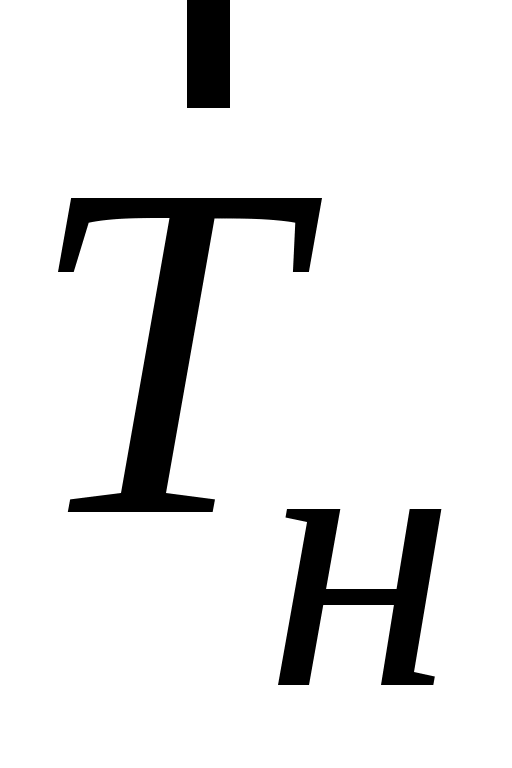 разматывающейся со шкива нити создаст вращающий момент сил
разматывающейся со шкива нити создаст вращающий момент сил  . При симметричном расположении грузов на крестовине можно считать, что действующая на маятник сила тяжести приложена к точке на оси вращения, а значит ее момент относительно этой оси равен нулю.
. При симметричном расположении грузов на крестовине можно считать, что действующая на маятник сила тяжести приложена к точке на оси вращения, а значит ее момент относительно этой оси равен нулю.
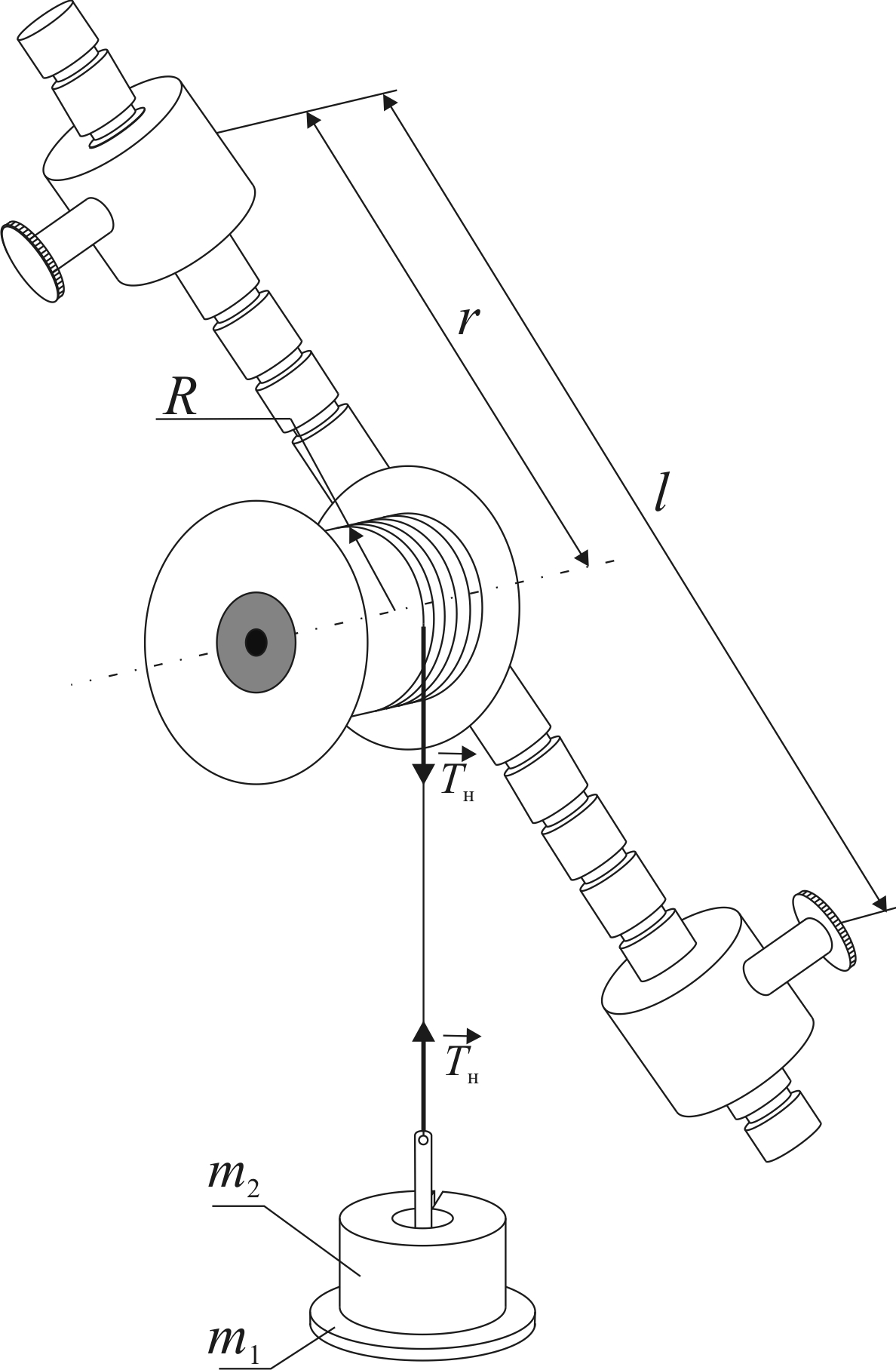
Рис. 2.3. Маятник Обербека
На рис. 2.4 представлены три основных состояния маятника Обербека. Пусть в начальный момент времени (t = 0) неподвижная платформа с грузом находится на высоте h1. Полная механическая энергия груза будет определяться потенциальной энергией:
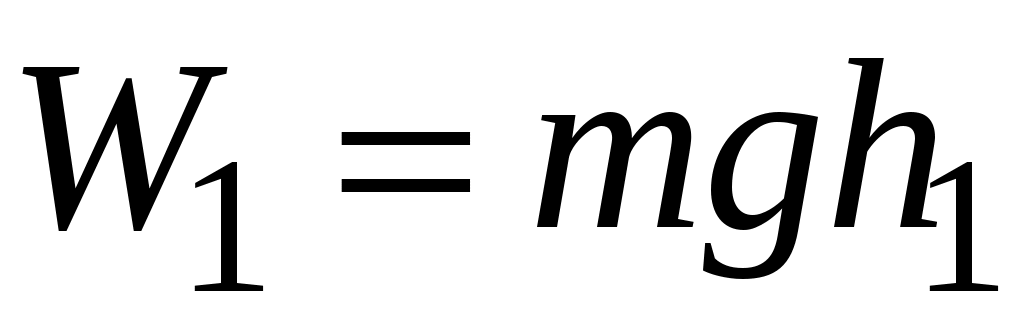 . (2.16)
. (2.16)
При движении груза потенциальная энергия переходит в кинетическую энергию платформы с грузом и кинетическую энергию вращения маятника. В момент времени t1, когда платформа с грузом подходит к нижнему положению, механическая энергия системы «маятник Обербека и платформа с грузом» равна:
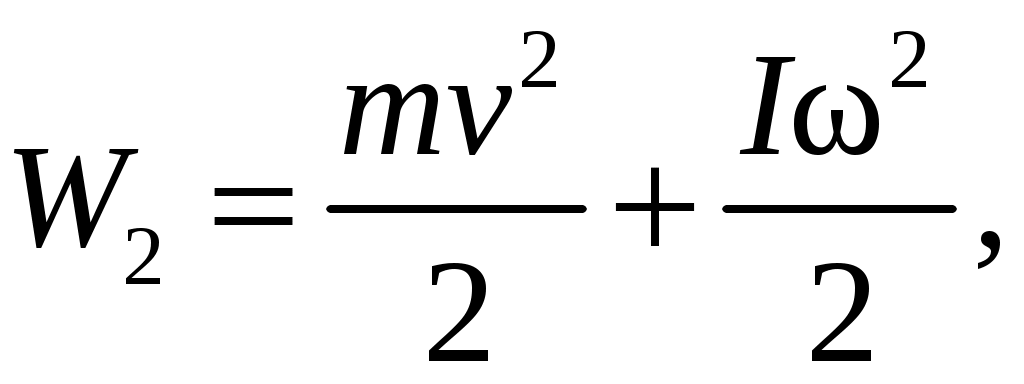
(2.17)
где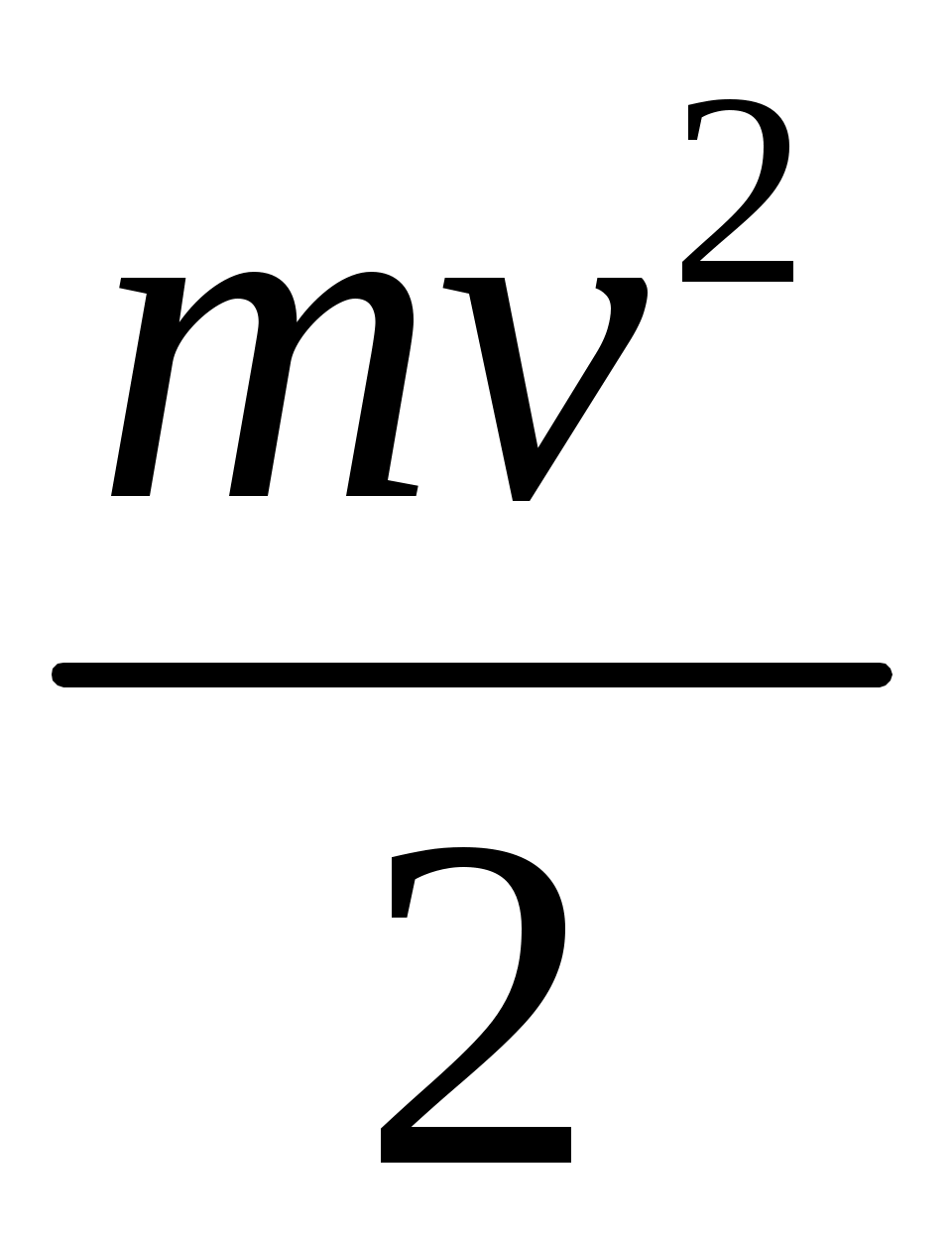 – кинетическая энергия поступательного движения платформы с грузом;
– кинетическая энергия поступательного движения платформы с грузом;
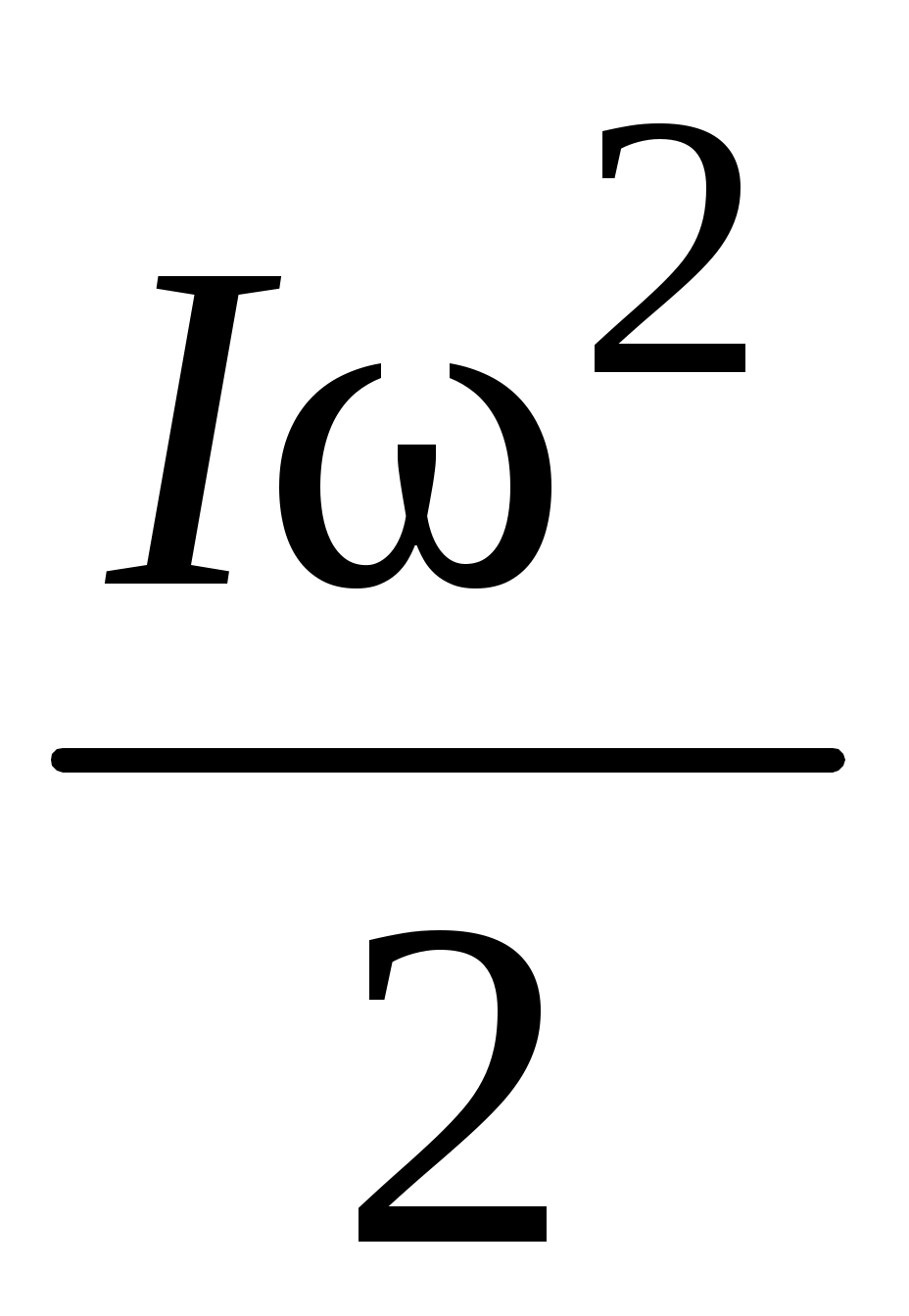 – кинетическая энергия вращения маятника Обербека;
– кинетическая энергия вращения маятника Обербека;
I – момент инерции маятника относительно оси вращения;
– угловая скорость вращения;
v – скорость движения платформы с грузом.
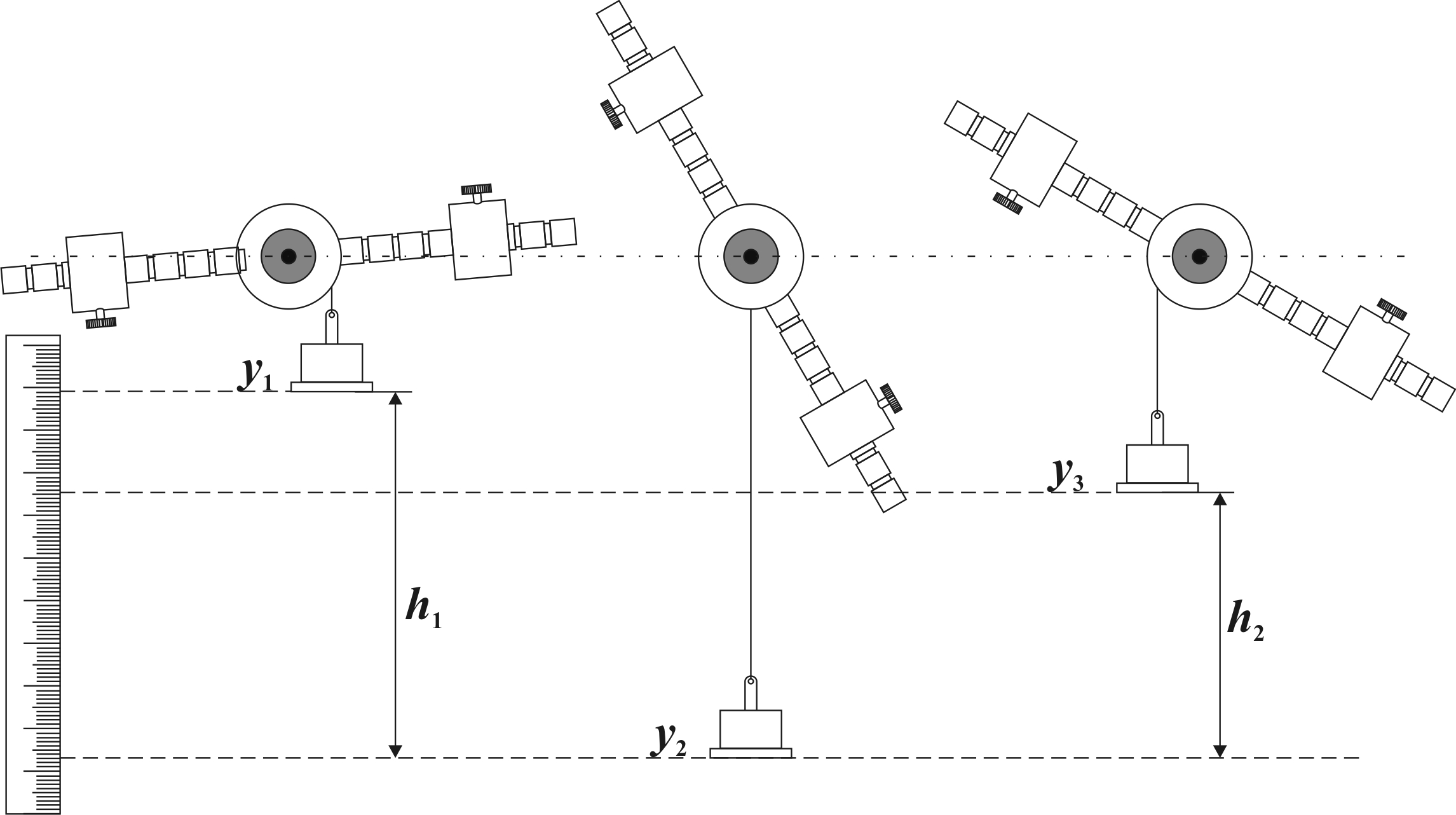
Рис. 2.4. Маятник Обербека в трех основных положениях
В крайнем нижнем положении (когда нить полностью размотана) груз с платформой меняет направление скорости на противоположное. При этом мы полагаем, что модуль скорости, а значит и кинетическая энергия платформы с грузом не меняется, так как считаем нить абсолютно упругой.
При вращении маятника и движении груза действует сила сопротивления воздуха, а в подшипниках действуют силы трения. Сопротивлением воздуха мы пренебрегаем и считаем, что силы трения дают постоянный тормозящий момент MТР. Наличие сил трения приводит к тому, что при движении маятника часть механической энергии постоянно переходит во внутреннюю энергию.
Работа момента силы трения при спуске платформы с грузом, в соответствии с (2.15), равна:
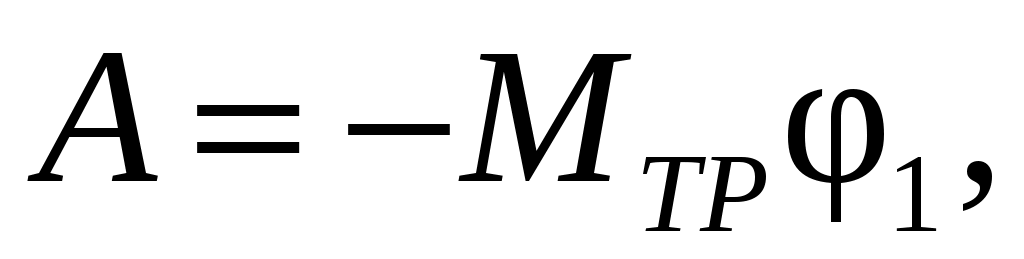 (2.18)
(2.18)
где φ1 – угол поворота шкива при перемещении платформы с грузом на расстояние h1;
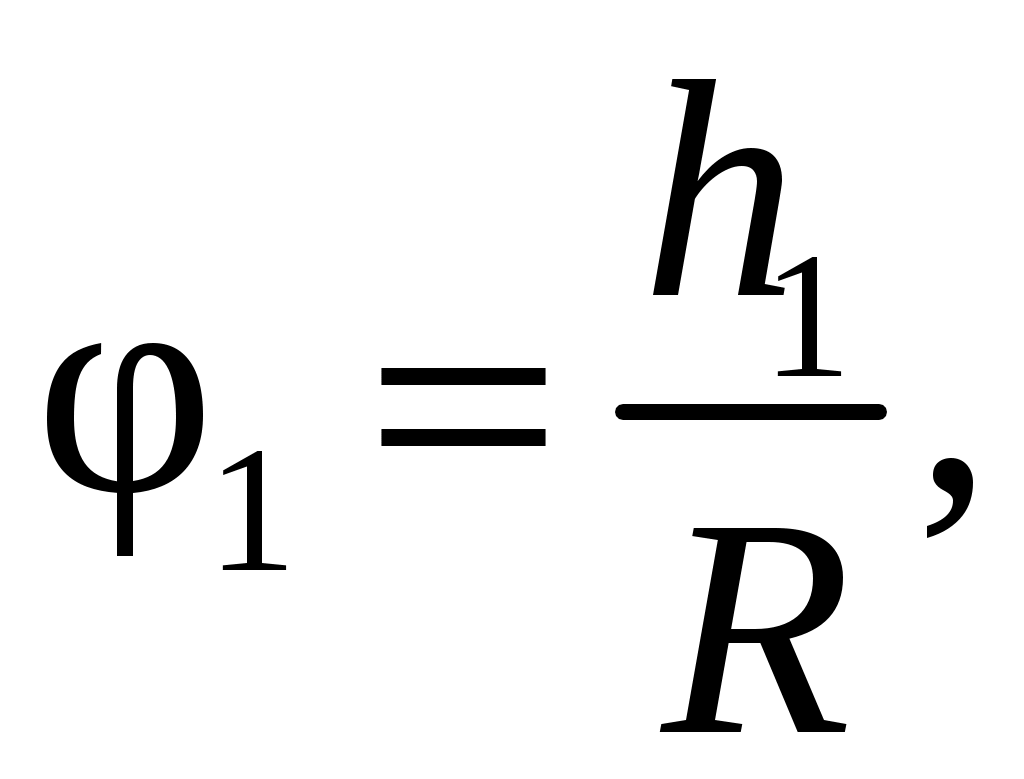 (2.19)
(2.19)
где R – радиус шкива.
Убыль механической энергии системы при спуске платформы равна работе момента неконсервативной силы трения:
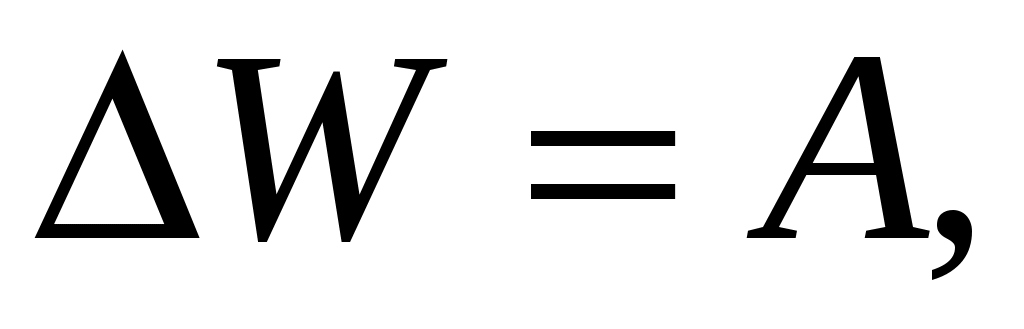 (2.20)
(2.20)
где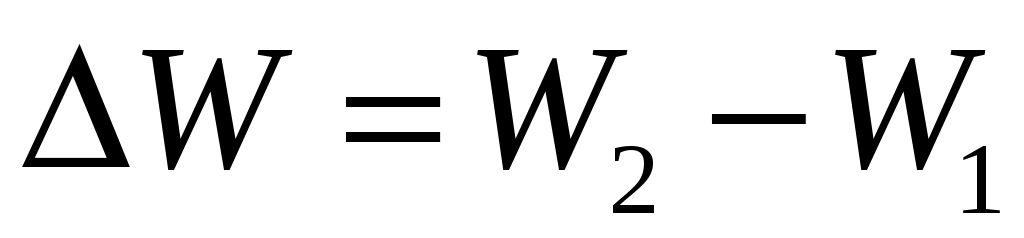 . Отсюда, с учетом (2.16), (2.17), (2.18) и (2.19), получим:
. Отсюда, с учетом (2.16), (2.17), (2.18) и (2.19), получим:
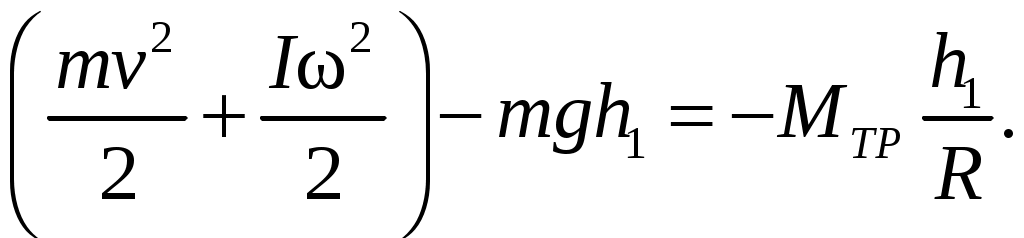 (2.21)
(2.21)
После того, как груз достигает нижней точки, маятник продолжает вращаться в ту же сторону и поднимает платформу с грузом на высоту h2, причем h2 < h1. При этом система будет обладать механической энергией:
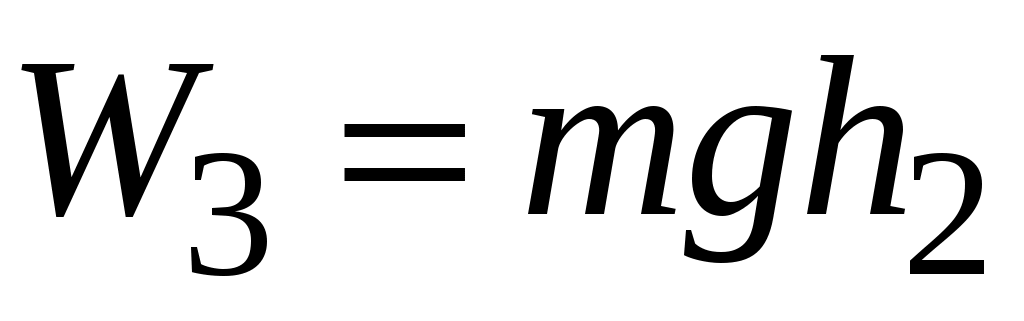
. (2.22)
Убыль механической энергии системы равна работе момента сил трения при вращении маятника на всем пути движения груза вниз и вверх:
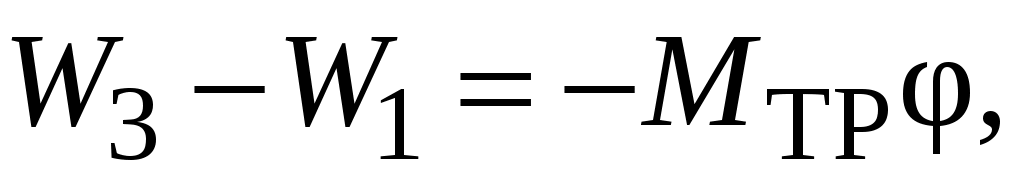 (2.23)
(2.23)
где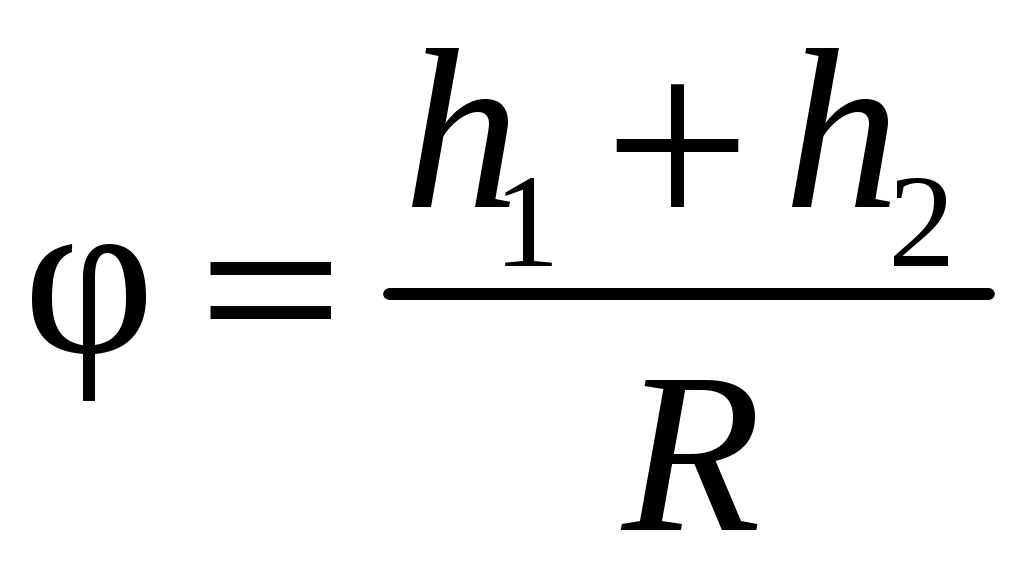 – угол поворота маятника при движении груза вниз на расстояние h1 и вверх на расстояние h2, исходя из того что
– угол поворота маятника при движении груза вниз на расстояние h1 и вверх на расстояние h2, исходя из того что 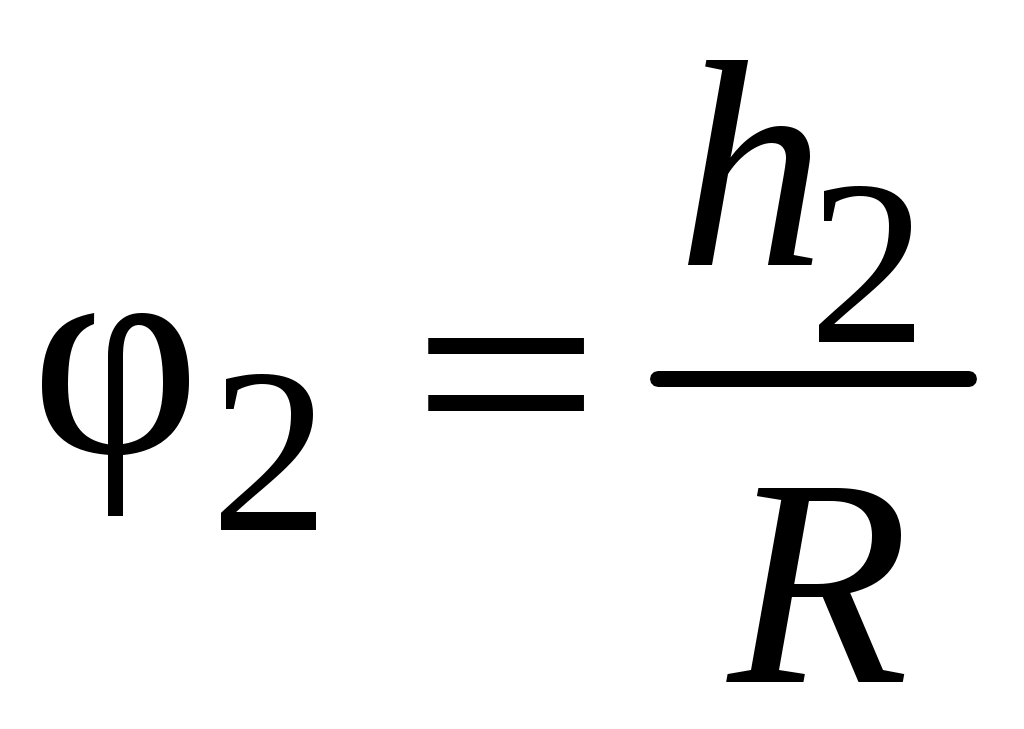 , а
, а 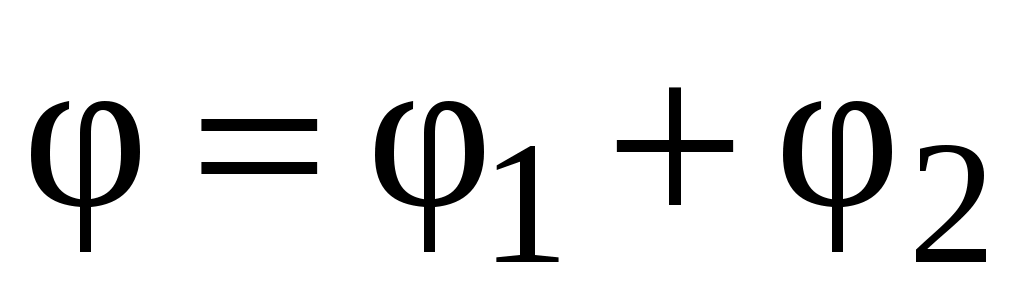 .
.
С учетом (2.22) и (2.16), выражение (2.23) записывается так:
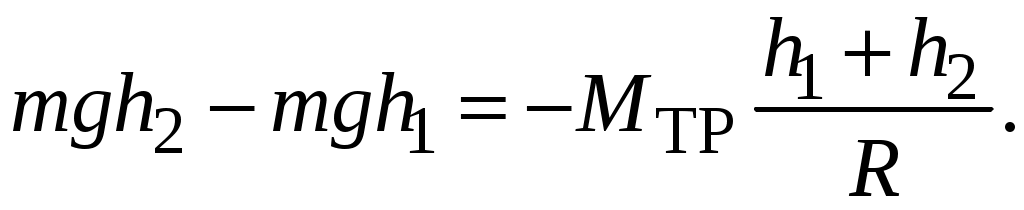 (2.24)
(2.24)
Отсюда:
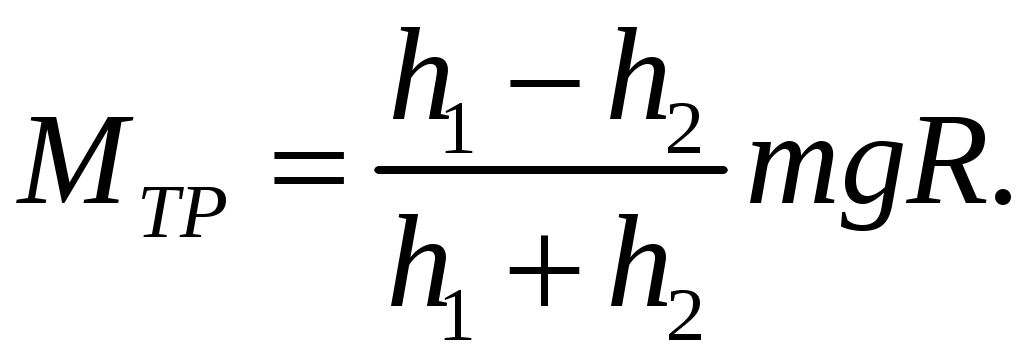 (2.25)
(2.25)
Так как движение груза вниз - равноускоренное с начальной скоростью, равной нулю, то в низшей точке скорость груза:
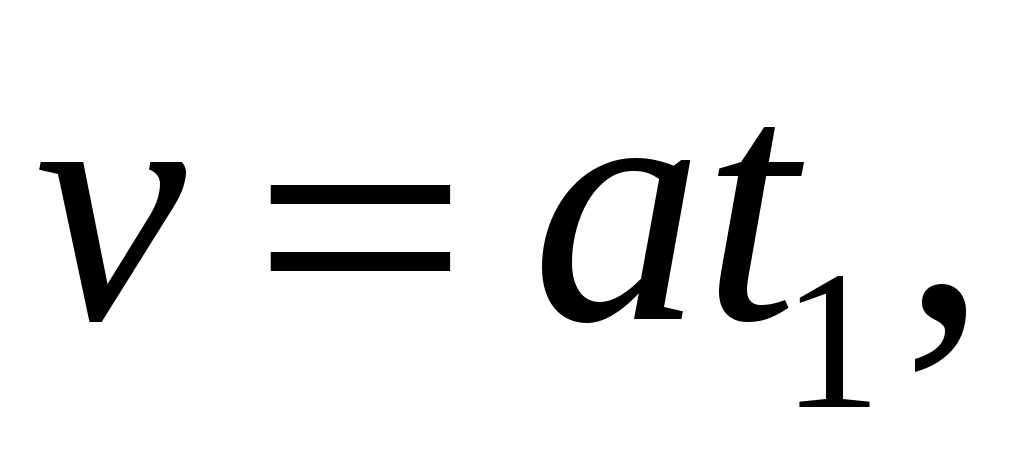 (2.26)
(2.26)
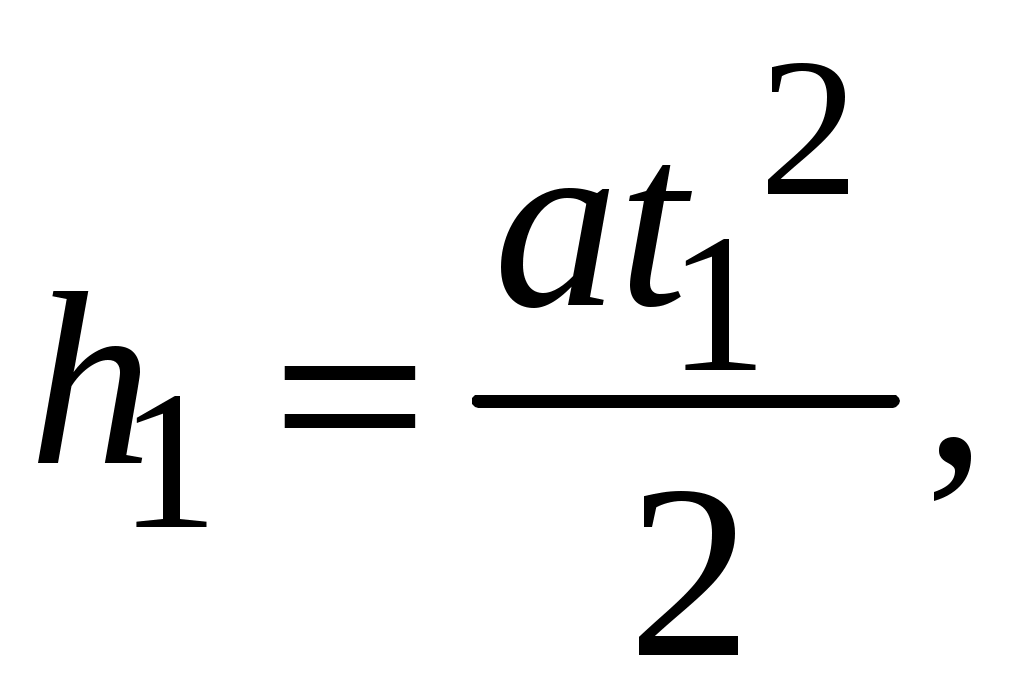 (2.27)
(2.27)
где а – ускорение платформы с грузом;
t1 – время опускания груза.
Из уравнений (2.26) и (2.27) можно получить:
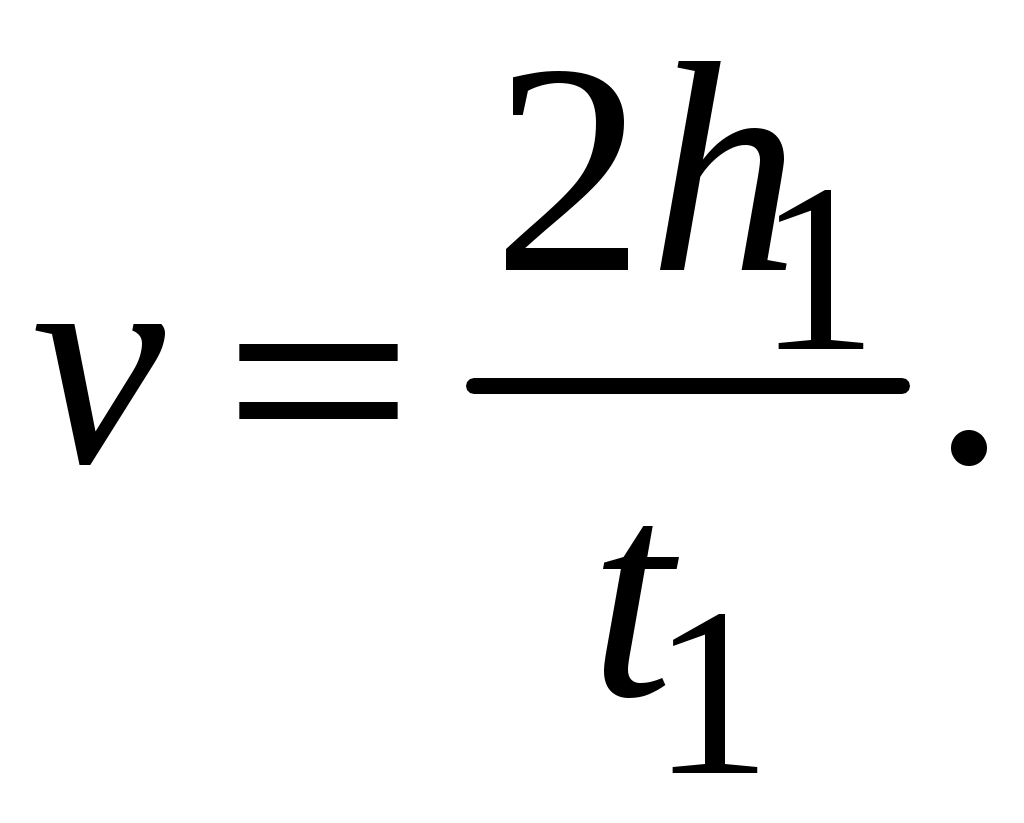 (2.28)
(2.28)
Поскольку нить при движении груза разматывается со шкива без скольжения, линейная скорость точек, лежащих на поверхности шкива, равна скорости движения груза. Известно, что модуль угловой скорости связан с модулем линейной скорости движения точки по окружности равенством:
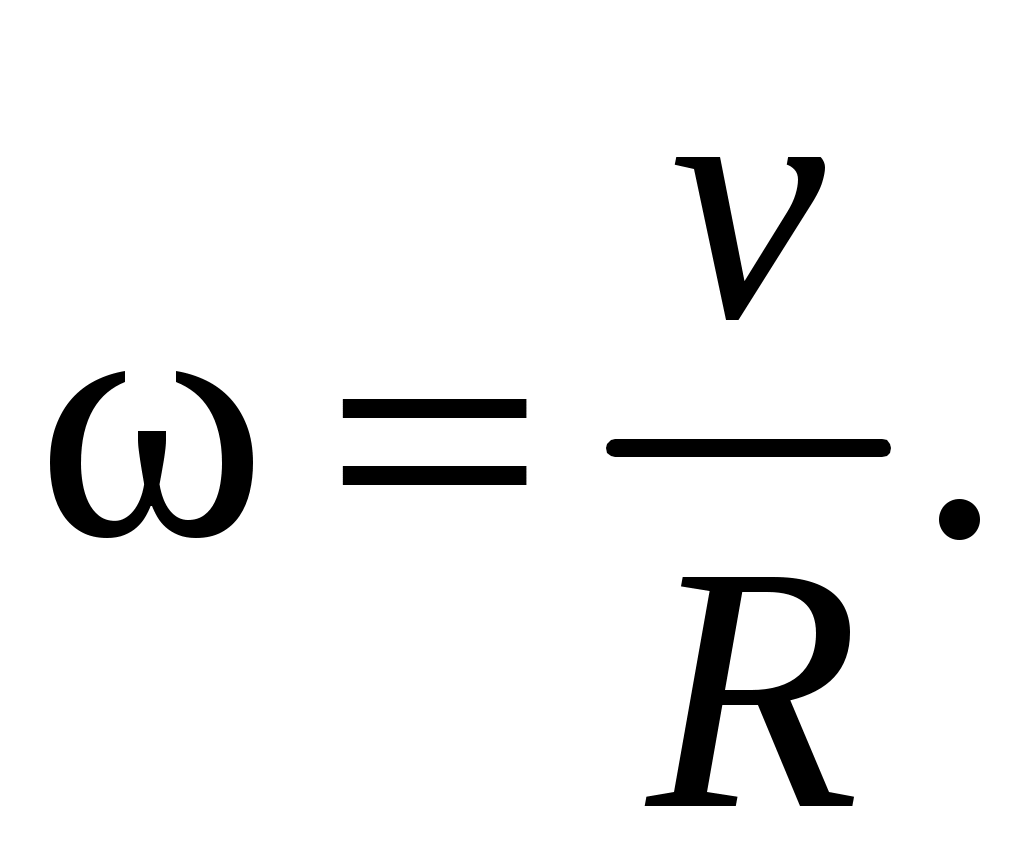 (2.29)
(2.29)
Подставив значение линейной скорости (2.28) в (2.29), получим:
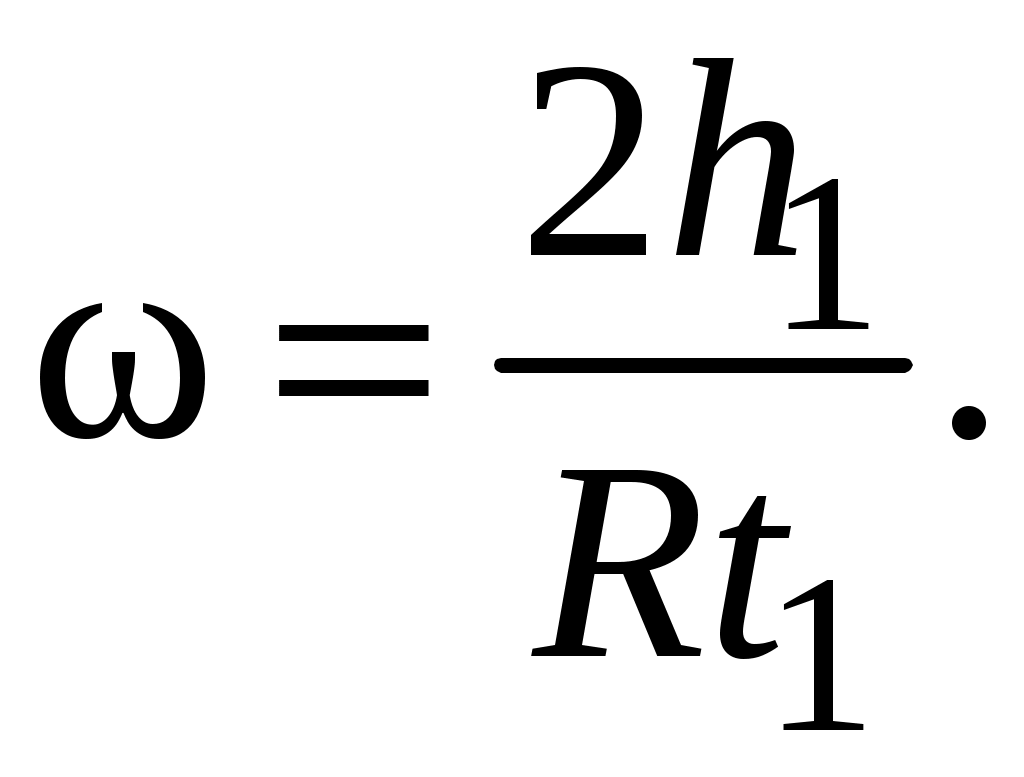 (2.30)
(2.30)
Подставив в уравнение (2.21) значения MТР (2.25), υ (2.28), ω (2.30), после преобразований получим расчетную формулу для вычисления момента инерции маятника Обербека:
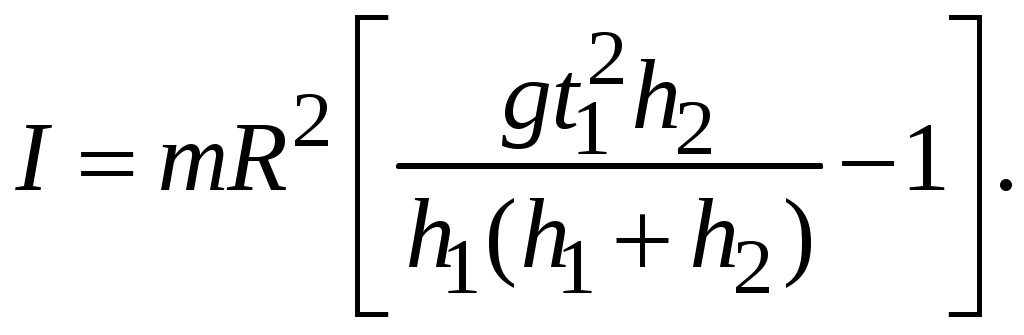 (2.31)
(2.31)
Порядок выполнения лабораторной работы
1. Закрепите грузы на крестовинах на одинаковых расстояниях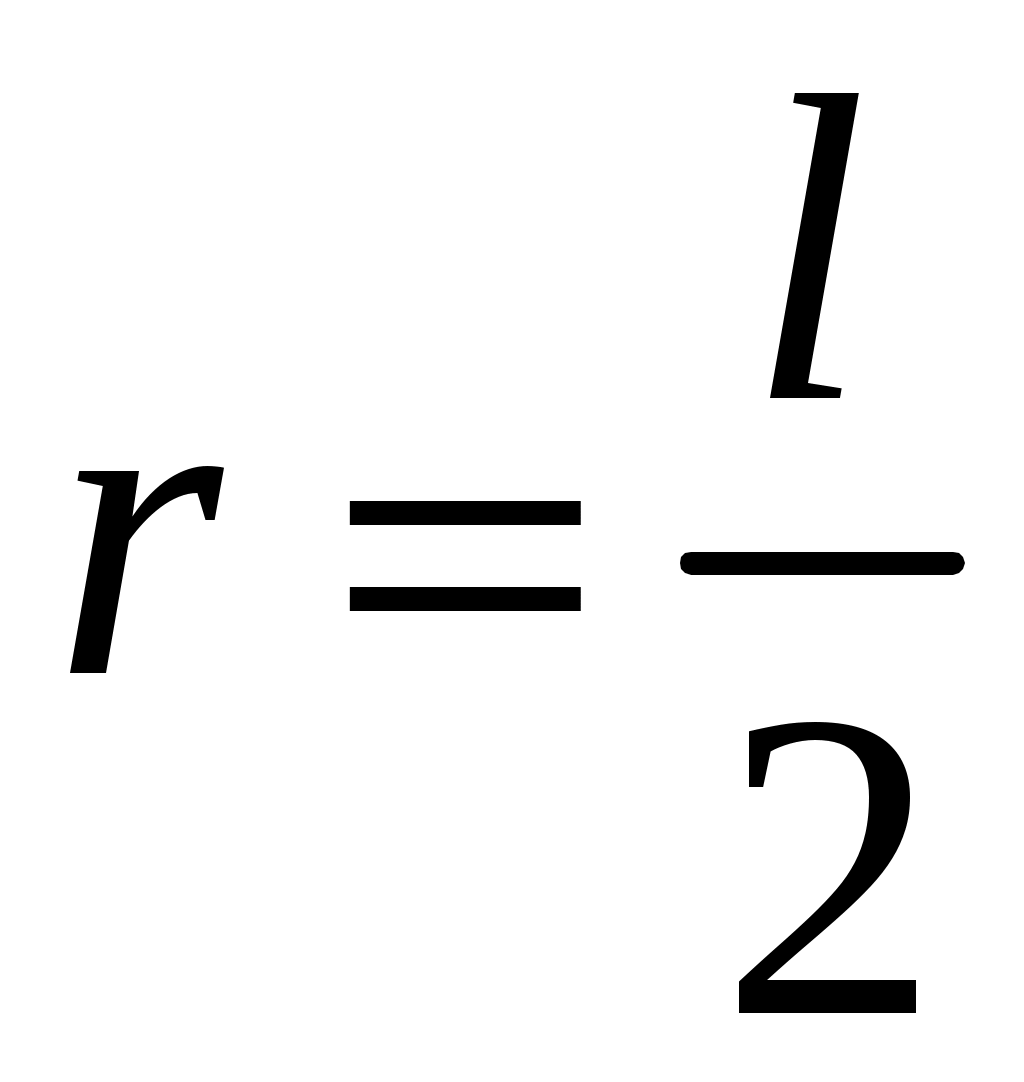 от оси вращения (рис. 2.3).
от оси вращения (рис. 2.3).
– угловая скорость вращения.
Моментом инерции тела относительно оси z называется скалярная величина:
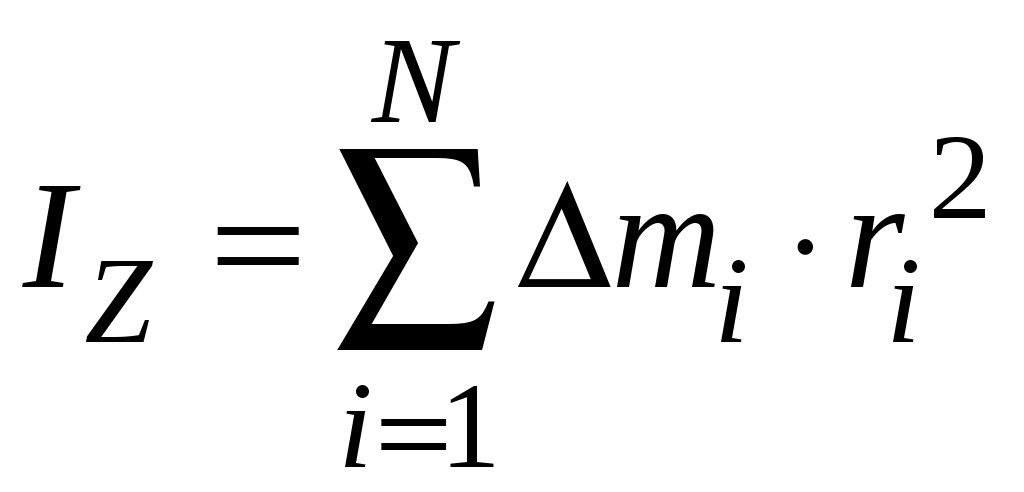 .
.Здесь считается, что мы мысленно разбили тело на очень большое число N оченьмаленьких кусочков, каждый из которых можно считать материальной точкой, при этом
mi – масса i-го кусочка;
ri – расстояние от i-го кусочка до оси z.
На самом деле, момент инерции тела относительно оси zесть тройной интеграл, вычисляемый по всему объему тела:
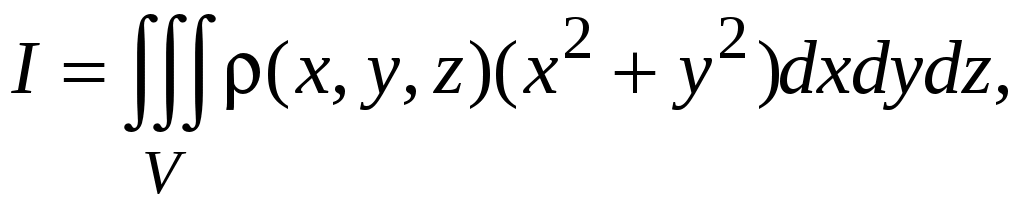
где
Момент инерции – величина аддитивная, то есть момент инерции системы из N тел относительно оси равен сумме моментов инерции всех тел системы относительно той же оси:
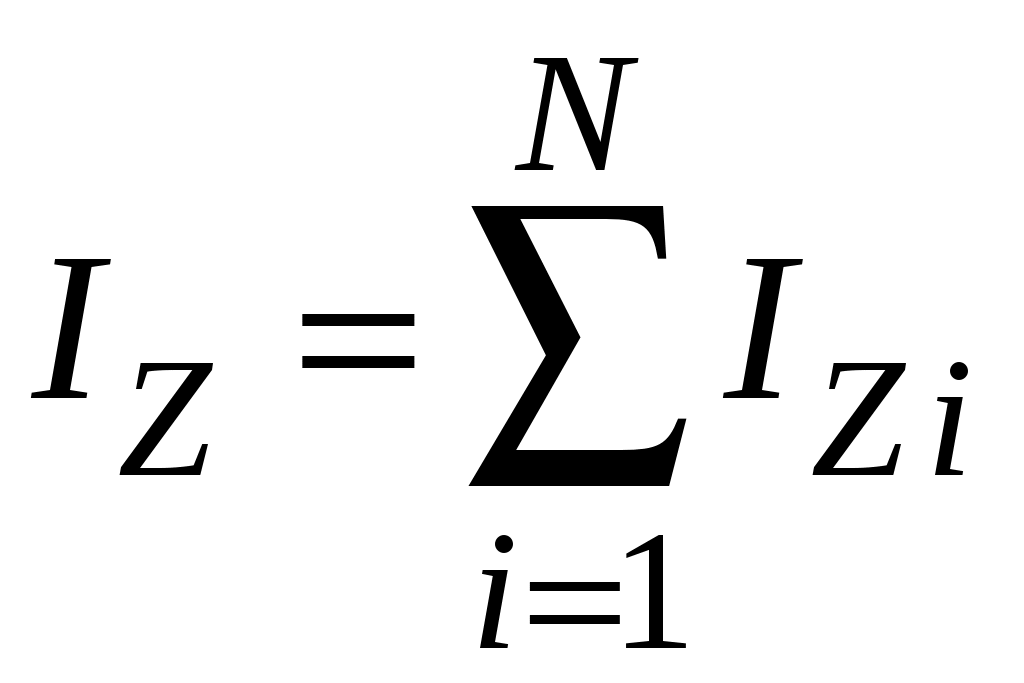 .
.Момент инерции материальной точки относительно оси z, очевидно, равен:
где m – масса материальной точки;
r – расстояние от точки до данной оси.
Формулы для вычисления моментов инерции простейших симметричных абсолютно твердых тел приведены в табл. 2.1.
Таблица 2.1
| Тело | Параметры тела | Ось z, относительно которой вычислен момент инерции | Момент инерции |
| Тонкий однородный стержень | m – масса; l – длина | Ось, проходящая перпендикулярно к стержню через его середину | |
| Ось, проходящая перпендикулярно к стержню через его конец | 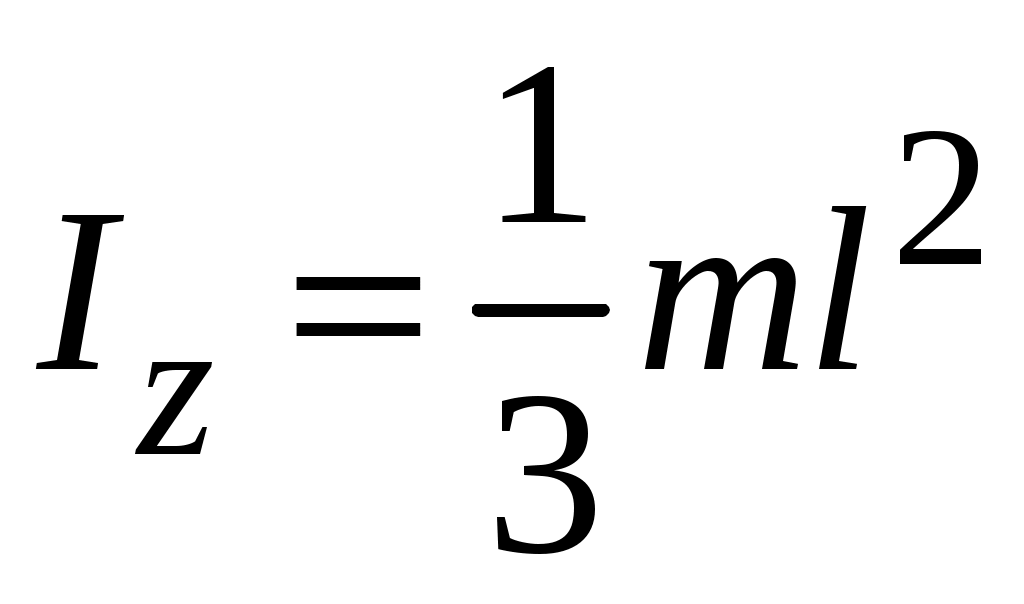 | ||
| Тонкий обруч | m – масса; R – радиус | Ось, проходящая через центр перпендикулярно плоскости обруча | |
| Полый тонкостенный цилиндр | m – масса; R – радиус | Ось цилиндра | |
Окончание табл. 2.1
| Тело | Параметры тела | Ось z, относительно которой вычислен момент инерции | Момент инерции |
| Диск | m – масса; R – радиус | Ось, проходящая через центр перпендикулярно плоскости диска | |
| Сплошной цилиндр | m – масса; R – радиус | Ось цилиндра | |
| Сплошной шар | m – масса; R – радиус | Любая ось, проходящая через центр | 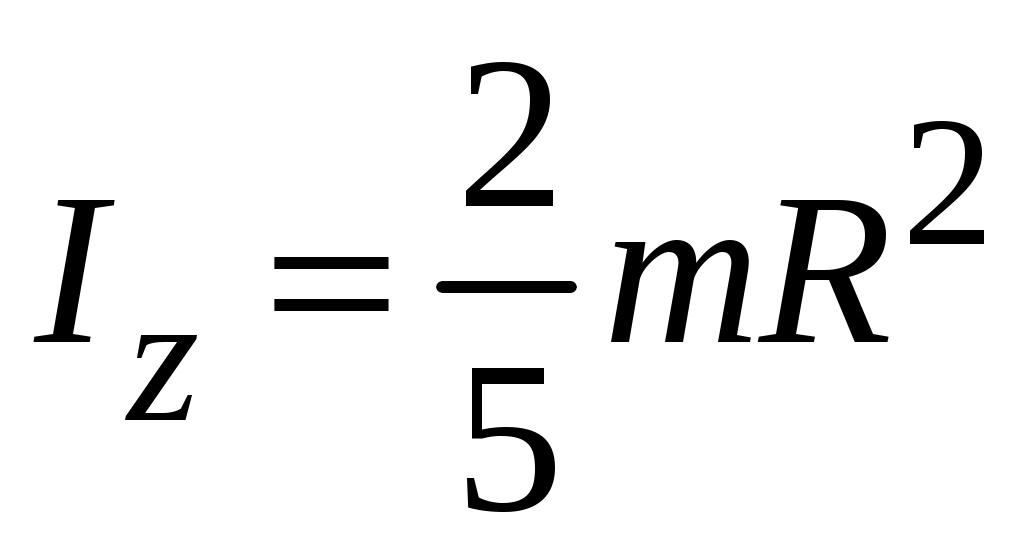 |
При вычислении моментов инерции часто используется теорема Штейнера:
где
m – масса тела;
a – расстояние между осями O иO'.
В случае, если твердое тело вращается вокруг оси z, его момент импульса относительно этой оси можно вычислить по формуле:
где
Можно показать, что при вращении тела вокруг неподвижной оси под действием силы элементарная работа силы определяется скалярным произведением вектора момента силы
где
– момент силы относительно оси вращения.
Следовательно, при повороте на конечный угол :
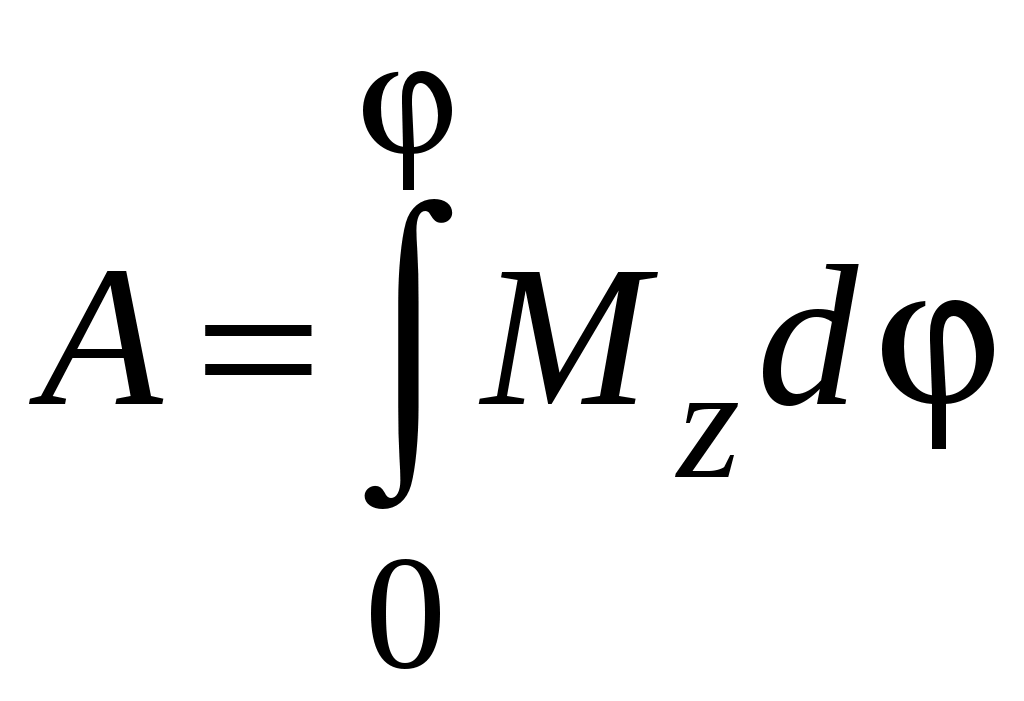 ,
,а если момент силы постоянен (
Экспериментальная установка и метод измерения
На рис. 2.3 представлен маятник Обербека, состоящий из двух стержней и шкива радиусом R, закрепленных на горизонтальной оси вращения. По стержням могут перемещаться и симметрично закрепляются в нужном положении два (по одному на каждом стержне) груза одинаковой массы.
На шкив наматывается нить, к концу которой крепится платформа с грузом. Примем массу платформы m1, а массу груза m2, в результате общая масса m = m1 + m2.
Если груз m поднять, намотав нить на шкив, на некоторую высоту h1 и отпустить, то груз придет в движение, а сила натяжения

Рис. 2.3. Маятник Обербека
На рис. 2.4 представлены три основных состояния маятника Обербека. Пусть в начальный момент времени (t = 0) неподвижная платформа с грузом находится на высоте h1. Полная механическая энергия груза будет определяться потенциальной энергией:
При движении груза потенциальная энергия переходит в кинетическую энергию платформы с грузом и кинетическую энергию вращения маятника. В момент времени t1, когда платформа с грузом подходит к нижнему положению, механическая энергия системы «маятник Обербека и платформа с грузом» равна:
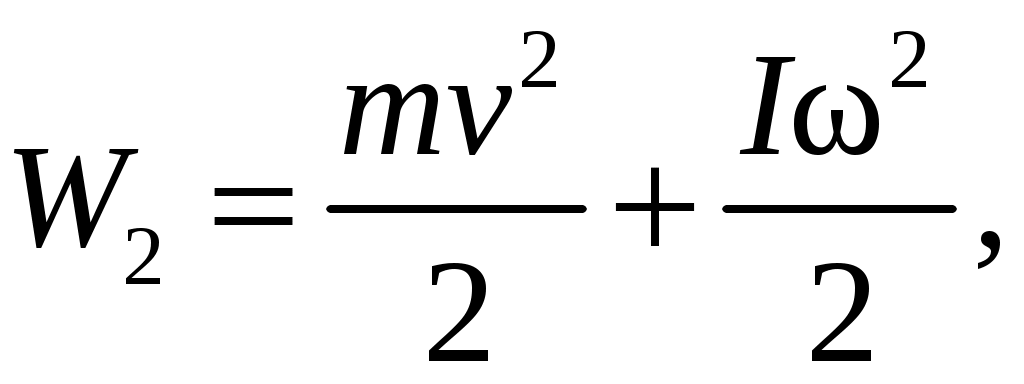
(2.17)
где
I – момент инерции маятника относительно оси вращения;
– угловая скорость вращения;
v – скорость движения платформы с грузом.

Рис. 2.4. Маятник Обербека в трех основных положениях
В крайнем нижнем положении (когда нить полностью размотана) груз с платформой меняет направление скорости на противоположное. При этом мы полагаем, что модуль скорости, а значит и кинетическая энергия платформы с грузом не меняется, так как считаем нить абсолютно упругой.
При вращении маятника и движении груза действует сила сопротивления воздуха, а в подшипниках действуют силы трения. Сопротивлением воздуха мы пренебрегаем и считаем, что силы трения дают постоянный тормозящий момент MТР. Наличие сил трения приводит к тому, что при движении маятника часть механической энергии постоянно переходит во внутреннюю энергию.
Работа момента силы трения при спуске платформы с грузом, в соответствии с (2.15), равна:
где φ1 – угол поворота шкива при перемещении платформы с грузом на расстояние h1;
где R – радиус шкива.
Убыль механической энергии системы при спуске платформы равна работе момента неконсервативной силы трения:
где
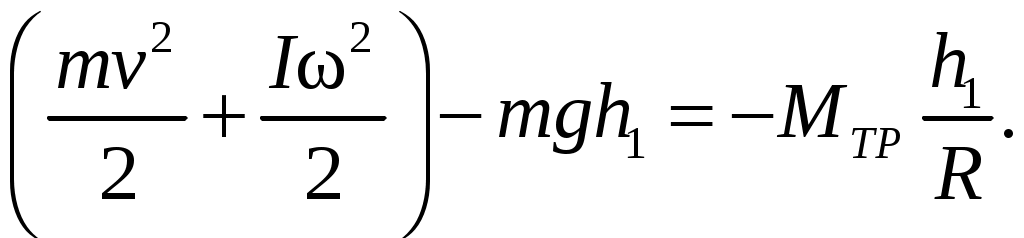 (2.21)
(2.21)После того, как груз достигает нижней точки, маятник продолжает вращаться в ту же сторону и поднимает платформу с грузом на высоту h2, причем h2 < h1. При этом система будет обладать механической энергией:
. (2.22)
Убыль механической энергии системы равна работе момента сил трения при вращении маятника на всем пути движения груза вниз и вверх:
где
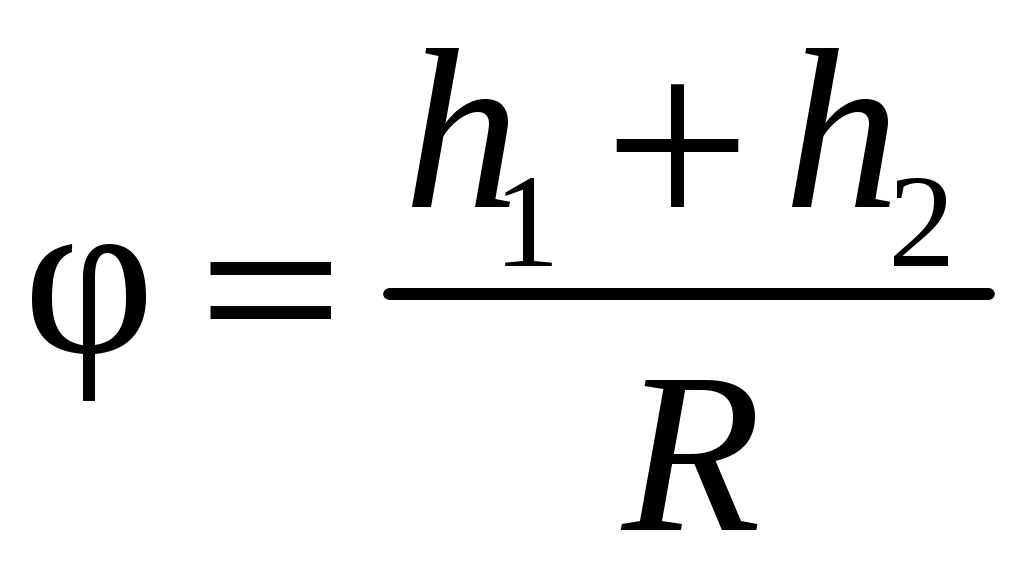 – угол поворота маятника при движении груза вниз на расстояние h1 и вверх на расстояние h2, исходя из того что
– угол поворота маятника при движении груза вниз на расстояние h1 и вверх на расстояние h2, исходя из того что 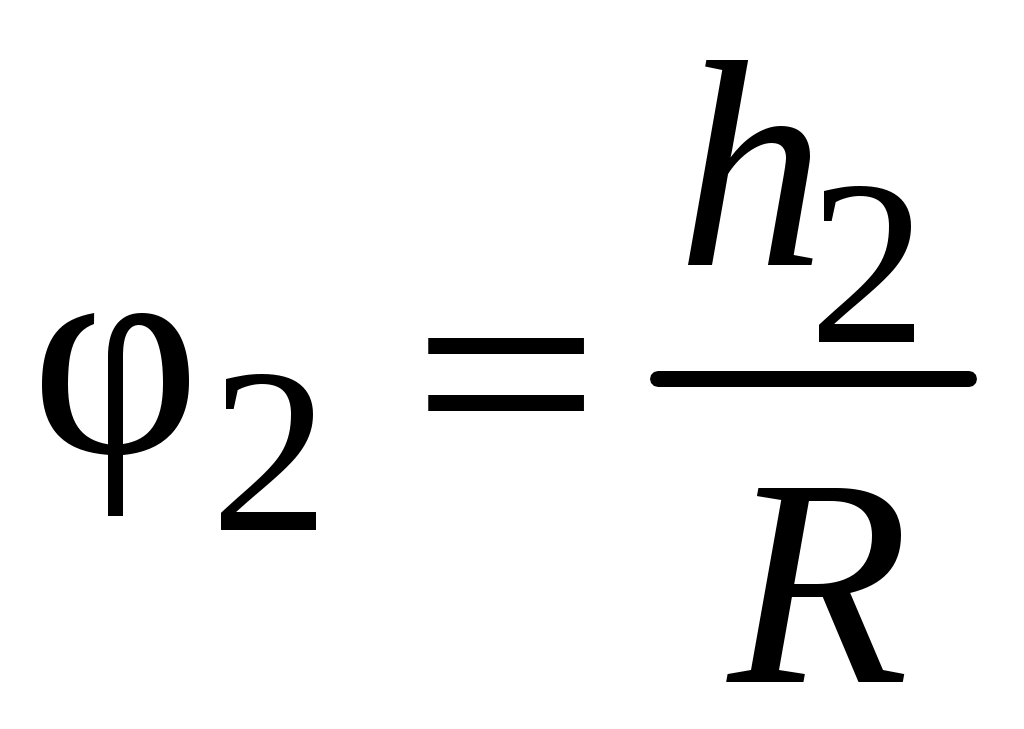 , а
, а С учетом (2.22) и (2.16), выражение (2.23) записывается так:
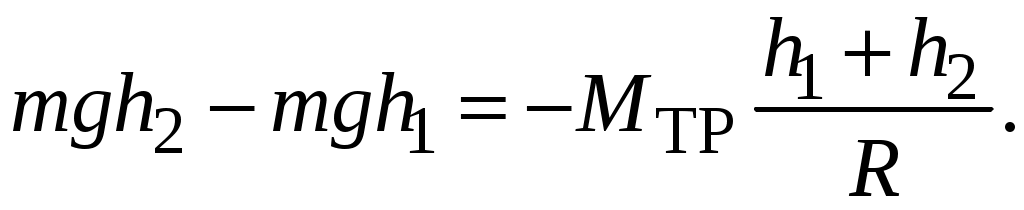 (2.24)
(2.24)Отсюда:
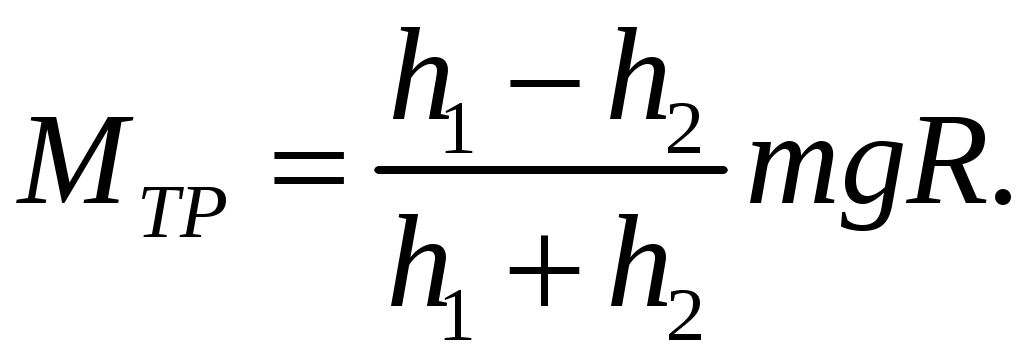 (2.25)
(2.25)Так как движение груза вниз - равноускоренное с начальной скоростью, равной нулю, то в низшей точке скорость груза:
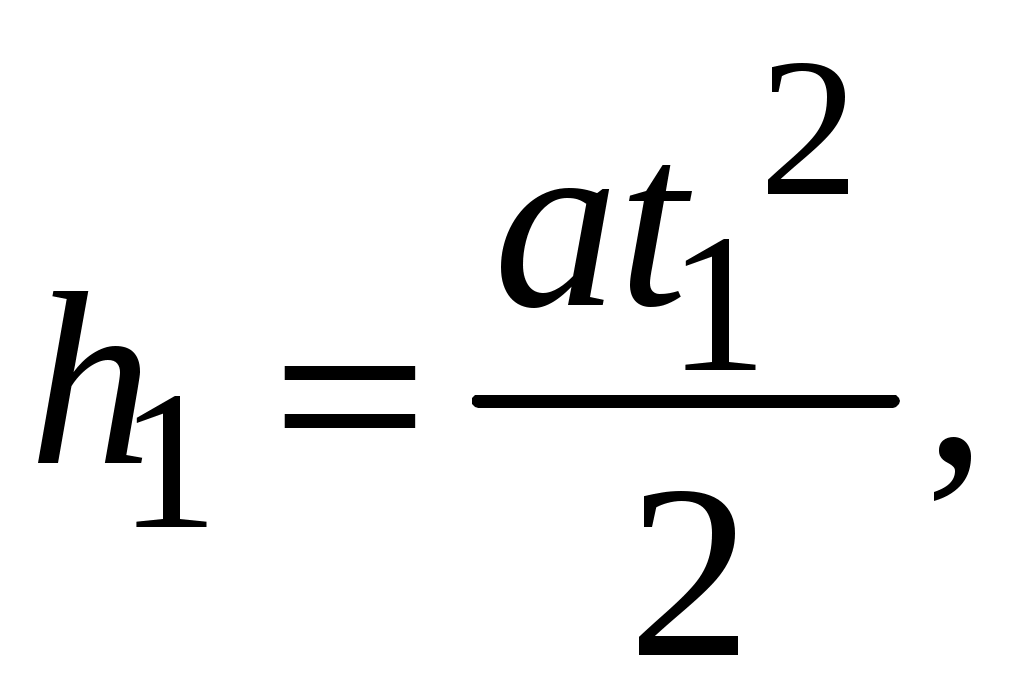 (2.27)
(2.27)где а – ускорение платформы с грузом;
t1 – время опускания груза.
Из уравнений (2.26) и (2.27) можно получить:
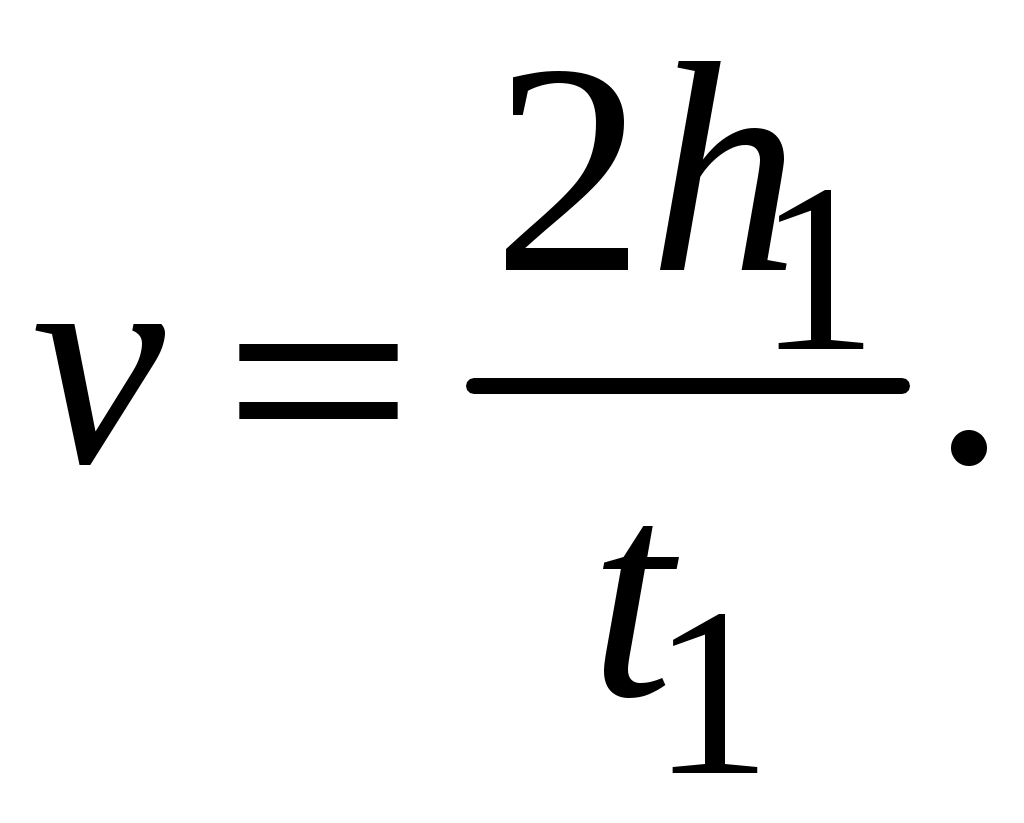 (2.28)
(2.28)Поскольку нить при движении груза разматывается со шкива без скольжения, линейная скорость точек, лежащих на поверхности шкива, равна скорости движения груза. Известно, что модуль угловой скорости связан с модулем линейной скорости движения точки по окружности равенством:
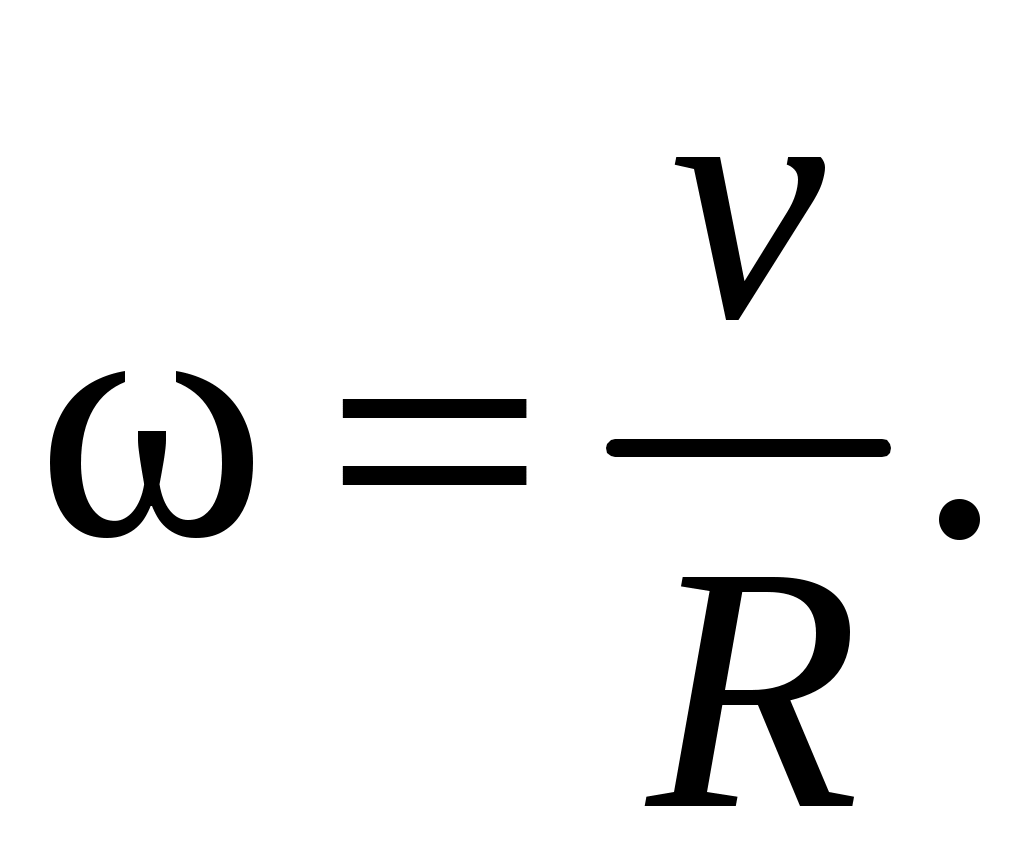 (2.29)
(2.29)Подставив значение линейной скорости (2.28) в (2.29), получим:
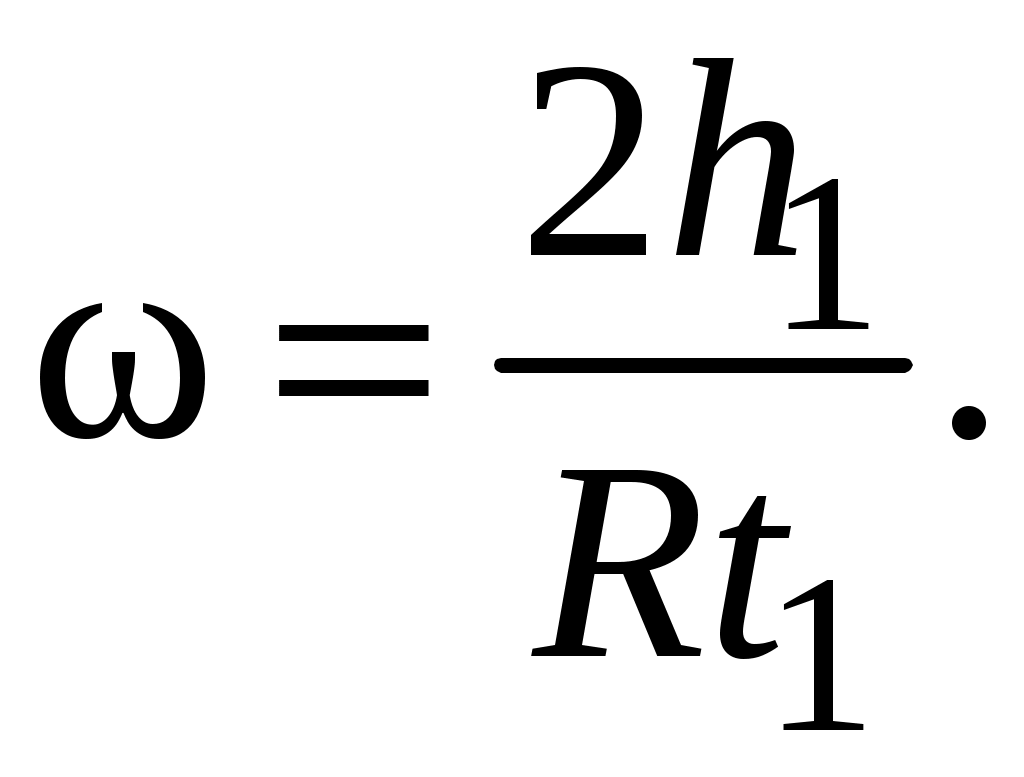 (2.30)
(2.30)Подставив в уравнение (2.21) значения MТР (2.25), υ (2.28), ω (2.30), после преобразований получим расчетную формулу для вычисления момента инерции маятника Обербека:
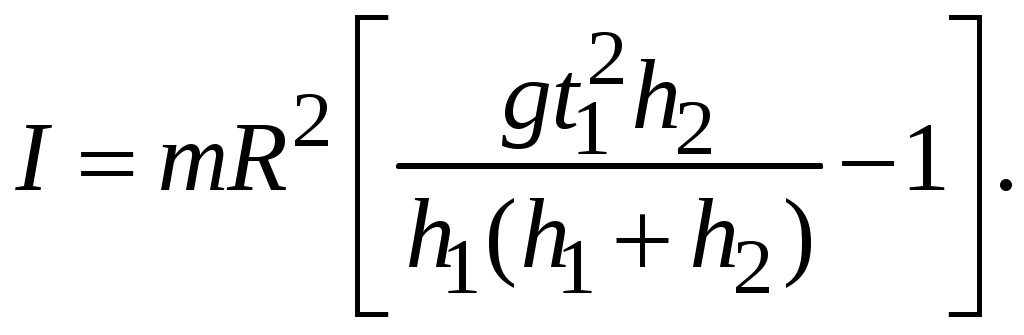 (2.31)
(2.31)Порядок выполнения лабораторной работы
1. Закрепите грузы на крестовинах на одинаковых расстояниях