ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 160
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Измерьте штангенциркулем радиус шкива, с которого разматывается нить.
3. На вертикальной шкале определите верхнее положение платформы с грузом y1 и нижнее положение платформы с грузом при полном разматывании нити y2. Определите высоту опускания груза с платформой
4. Отпустите платформу с грузом, засекая время.
5. Измерьте время t1 движения платформы с грузом до полного разматывания нити и высоту поднятия груза с платформой
Таблица 2.2
| h1= м R = мm = кг | |||||||
| № опыта | l, м | r, м | t, с | h2, м | I, кг · м2 | r2, м2 | I0, кг · м2 |
| 1 | | | | | | | |
| 2 | | | | | | | |
| 3 | | | | | | | |
| 4 | | | | | | | |
6. Измените симметрично расположение грузов на стержнях, поменяв расстояние r.
7. Повторите опыт четыре раза (пункты 4–6).
8. По формуле (2.31) вычислите момент инерции маятника в каждом опыте.
9. Результаты измерений и вычислений занесите в табл. 2.2.
10. Постройте в масштабе график зависимости момента инерции маятника Обербека I отквадрата расстояния r2закрепленных грузов до оси вращения (рис. 2.5).
11. Экспериментальные точки должны располагаться примерно вдоль прямой, но из-за случайных погрешностей будут присутствовать отклонения. Проведите прямую так, чтобы отклонения всех точек от нее в среднем были минимальны. Далее, продлите прямую до пересечения с осью ординат. Точка пересечения покажет
I0 –момент инерции маятника Обербека.
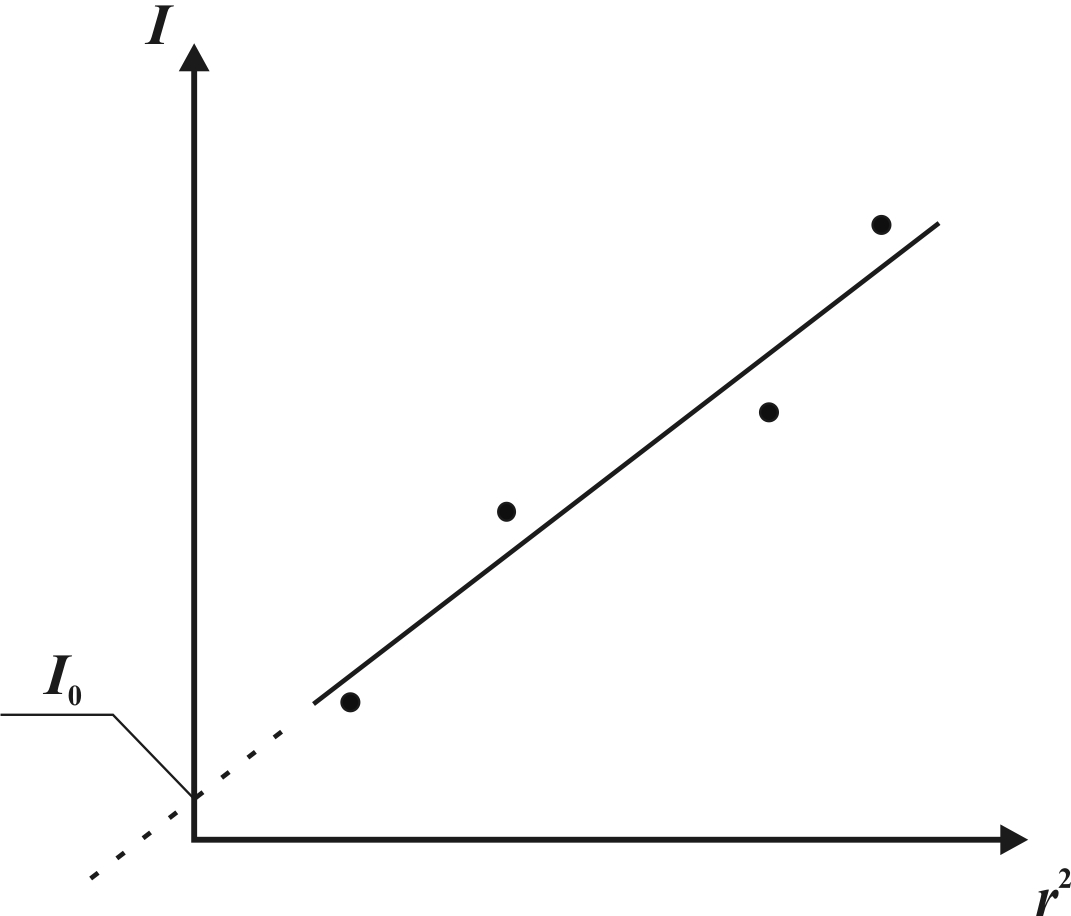
Рис. 2.5. График зависимости I (r2)
12. Сделайте вывод по проделанной работе и полученному результату.
Контрольные вопросы
-
Объясните зависимость момента инерции маятника от расположения грузов на стержнях. -
Каким было бы движение маятника при отсутствии трения? -
Чему равна работа при вращательном движении? -
Укажите значение полной механической энергии для трех важных состояний маятника Обербека (рис 2.4). -
Выведите расчетную формулу для момента инерции I.
Список литературы
1. Тюшев А. Н., Вылегжанина В. Д. Курс лекций по физике. Ч. 1. Механика : учеб. пособие. – Новосибирск : СГГА, 2011. – С. 53–74.
2. Савельев И. В. Курс общей физики. В 3 т. Т. 1. Механика. Молекулярная физика [Электронный ресурс] : учеб. пособие. – СПб. : Лань, 2016. – 436 с. – Режим доступа : http://e.lanbook.com/books/element. php?pl1_id=71760.
3. Трофимова Т. И. Курс физики : учеб. пособие. – М. : Академия, 2015. – 560 с.
3. Лабораторная работа № 21
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цели работы:
-
экспериментально исследовать квазистационарное электрическое поле, построить картину эквипотенциальных поверхностей и линий напряженности этого поля;
-
определить значение модуля напряженности электрического поля в указанных точках.
Приборы и принадлежности:
-
электролитическая ванна;
-
источник переменного напряжения;
-
потенциометр с зондом.
Подготовка к работе
По лекциям и приведенному ниже списку литературы изучите следующие вопросы:
-
закон Кулона;
-
понятие электрического поля;
-
напряженность электрического поля, линии напряженности;
-
потенциал электрического поля, эквипотенциальные линии;
-
связь между напряженностью поля и потенциалом.
Вопросы для допуска к работе
-
Что называется напряженностью электрического поля?
-
Что такое силовая линия электрического поля?
-
Что называется потенциалом электростатического поля?
-
Как расположены друг относительно друга в пространстве линии напряженности и эквипотенциальные поверхности?
-
Как связаны между собой напряженность и потенциал в данной точке?
-
Каковы условия равновесия зарядов на проводнике в электростатическом поле?
Теоретическое введение
Электрическое поле возникает в пространстве при наличии заряженных тел. Неподвижные заряды создают поле, которое называется электростатическим. В природе существуют электрические заряды двух знаков: положительные «+» и отрицательные «–», это наименование условно. Наименьшим зарядом обладают элементарные частицы, например: электрон – частица, входящая в состав атома, – имеет отрицательный заряд –е (здесь е = 1,6 ∙ 10-19 Кл – «элементарный заряд»), а протоны входящие в состав ядра атома, заряжены положительно (+е). Заряды одинакового знака отталкиваются друг от друга, заряды противоположных знаков – притягиваются.
По закону Кулона, силы взаимодействия двух точечных неподвижных зарядов q1 и q2 направлены вдоль прямой, их соединяющей, прямо пропорциональны величинам зарядов и обратно пропорциональны квадрату расстояния r12 между зарядами:
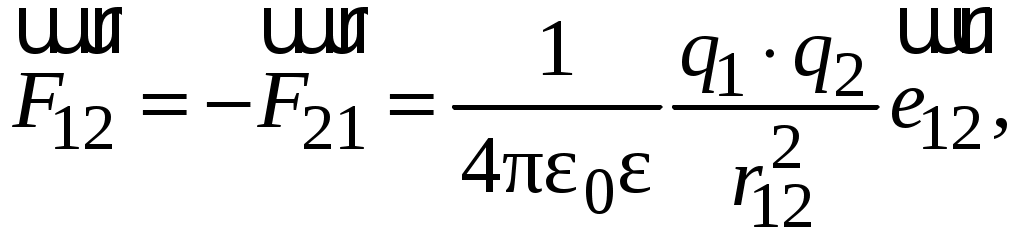 (3.1)
(3.1)
где 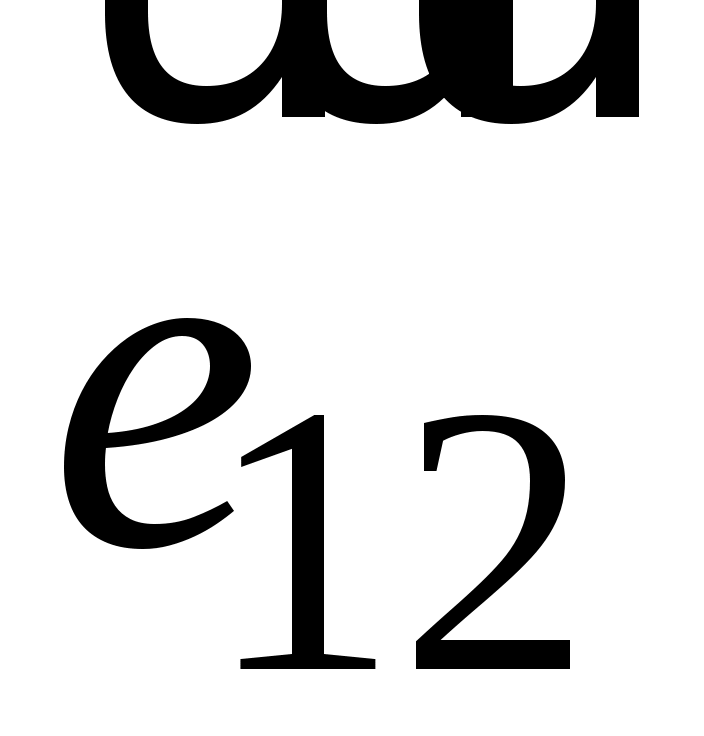 – единичный вектор, направленный от одного заряда к другому,
– единичный вектор, направленный от одного заряда к другому,
ε0 = 8,85 ∙ 10-12 Ф/м – электрическая постоянная,
ε – диэлектрическая проницаемость среды.
Эти силы являются центральными и, следовательно, консервативными.
Отношение силы, действующей на пробный заряд, к величине этого заряда не зависит от величины заряда и называется напряженностью электрического поля
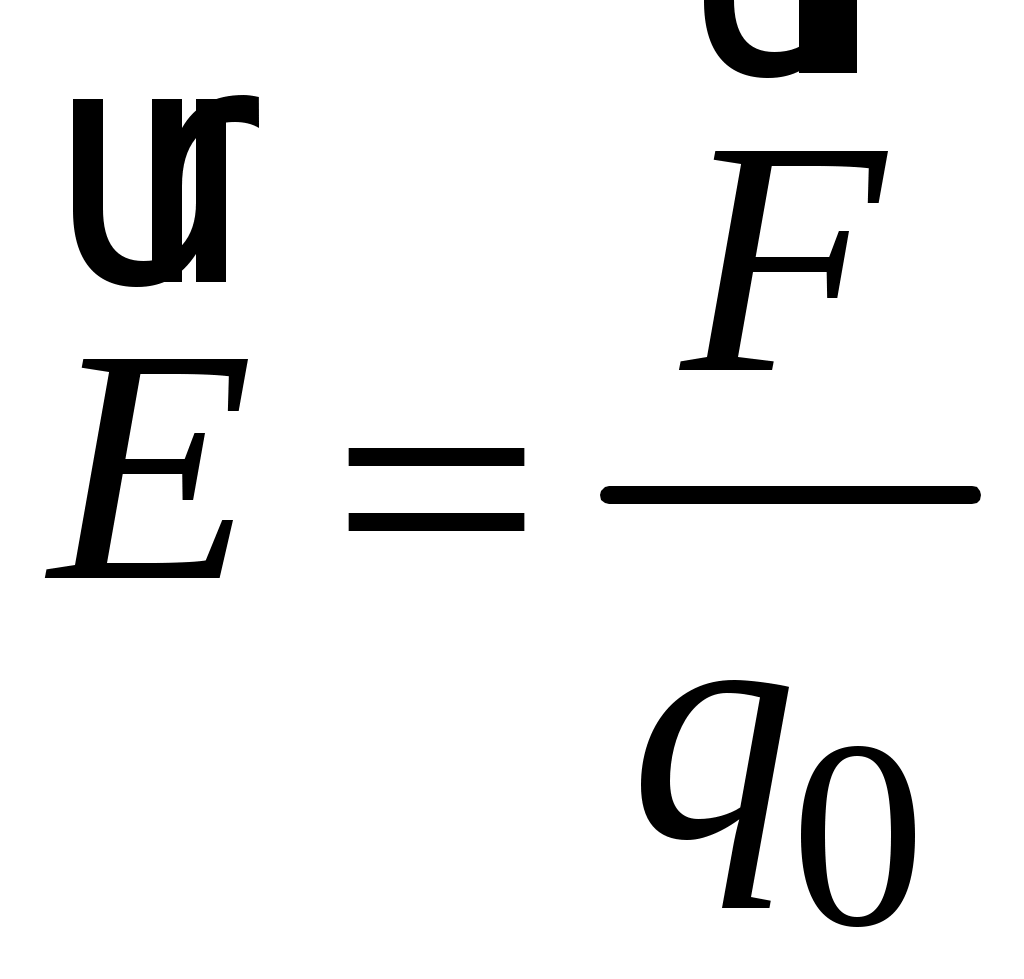 . (3.2)
. (3.2)
Напряженность 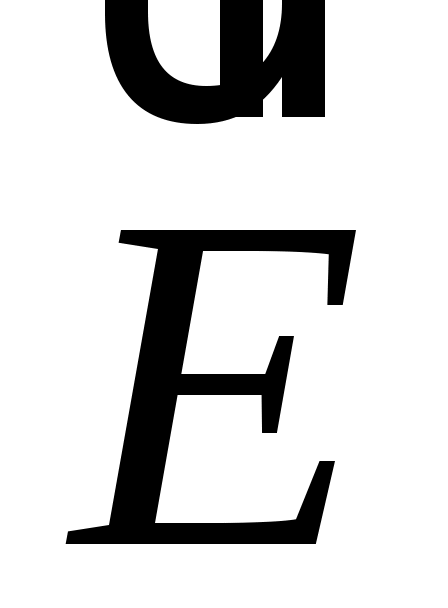 – векторная величина, ее направление совпадает с направлением силы
– векторная величина, ее направление совпадает с направлением силы 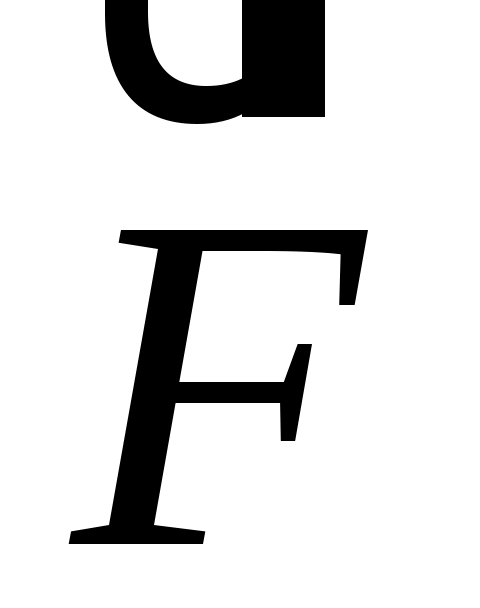 , действующей на пробный положительный заряд
, действующей на пробный положительный заряд 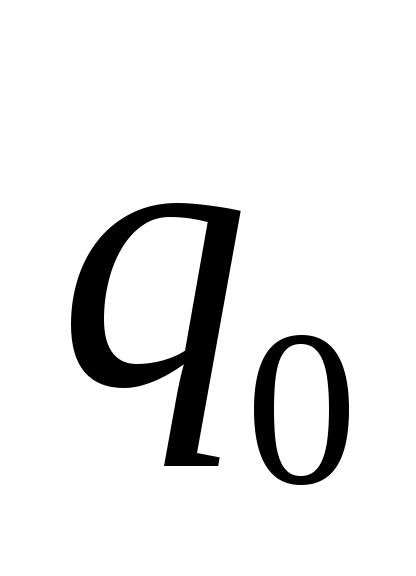 , находящийся в данной точке пространства.
, находящийся в данной точке пространства.
Электростатическое поле можно представить графически с помощью системы линий напряженности (силовых линий), начинающихся на положительных зарядах и заканчивающихся на отрицательных или уходящих на бесконечность. Вектор напряженности 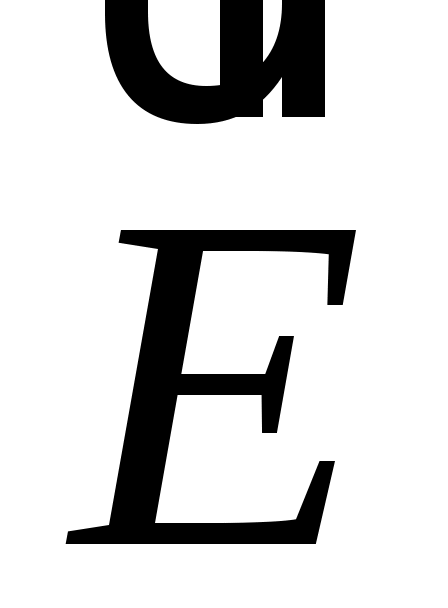 в каждой точке силовой линии направлен по касательной к ней и совпадает с ней по направлению. Густота силовых линий пропорциональна модулю вектора напряженности
в каждой точке силовой линии направлен по касательной к ней и совпадает с ней по направлению. Густота силовых линий пропорциональна модулю вектора напряженности 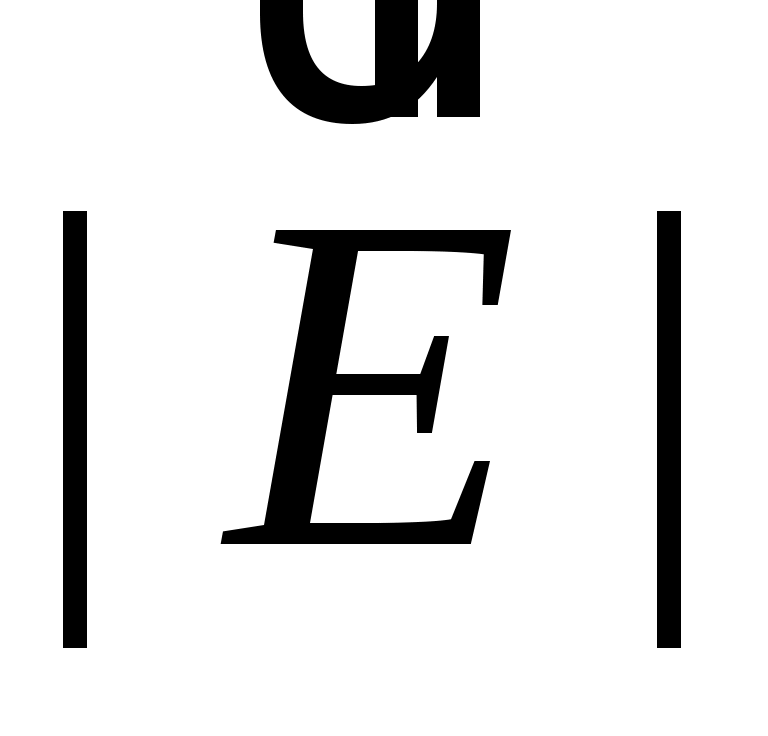 .
.
Сила, действующая на произвольный точечный заряд, помещенный в данную точку поля, определяется произведением величины этого заряда на напряженность электрического поля в данной точке
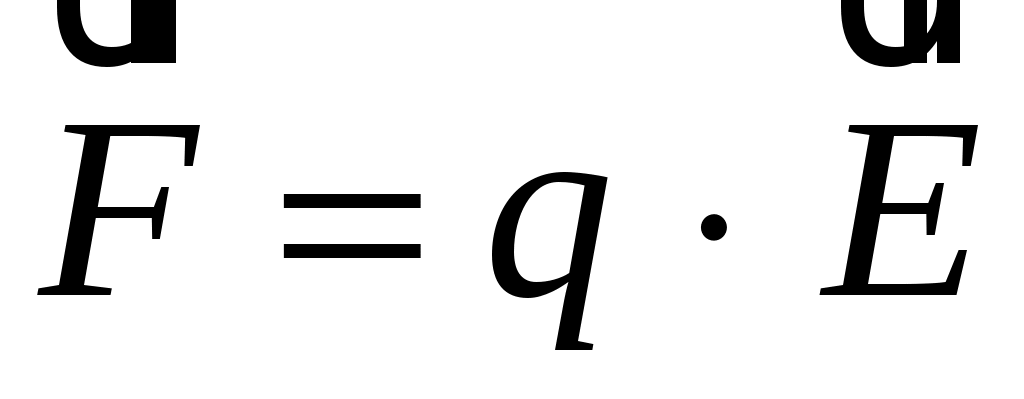 . (3.3)
. (3.3)
Работа консервативных электростатических сил по перемещению заряда в электростатическом поле не зависит от траектории движения, а определяется лишь начальным и конечным положением заряда, эта работа может быть выражена через изменение потенциальной энергии заряда со знаком «–»:
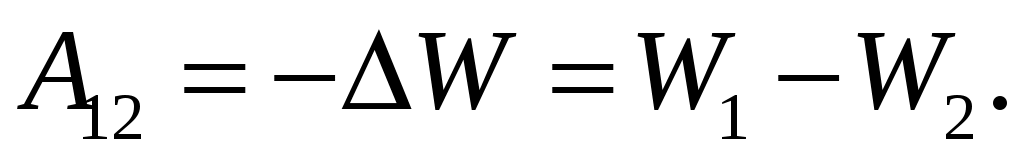 (3.4)
(3.4)
Потенциальная энергия 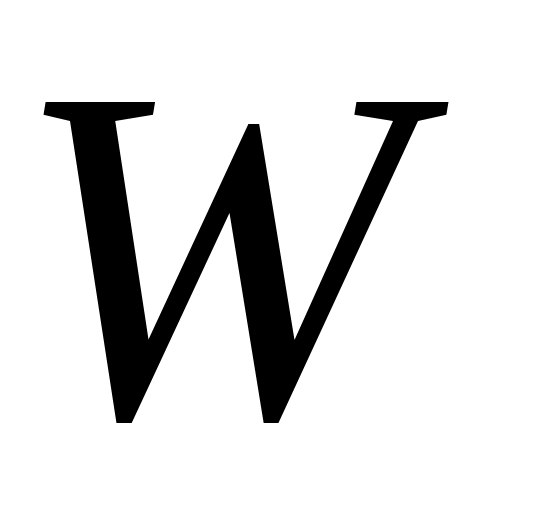 точечного заряда
точечного заряда 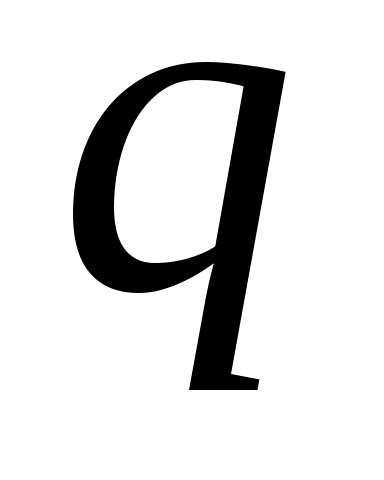 в электростатическом поле может быть выражена через энергетическую характеристику этого поля, называемую потенциалом φ, как произведение
в электростатическом поле может быть выражена через энергетическую характеристику этого поля, называемую потенциалом φ, как произведение 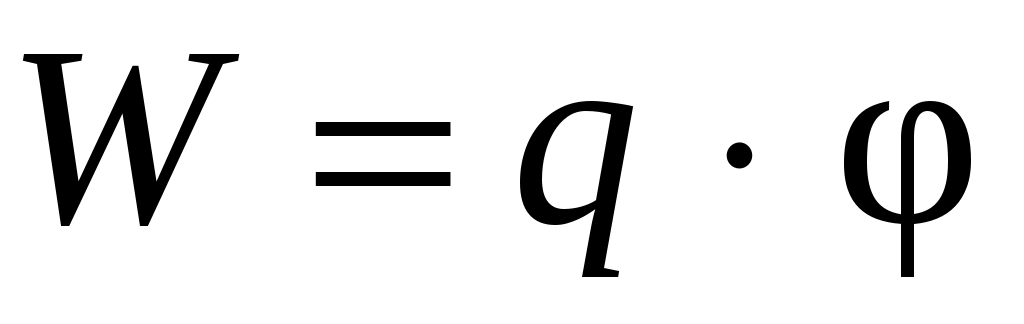 , следовательно, разность потенциалов
, следовательно, разность потенциалов 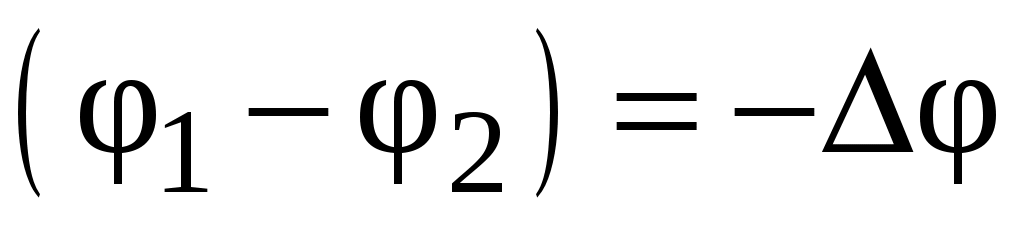 между точками 1 и 2 можно определить через отношение работы сил поля
между точками 1 и 2 можно определить через отношение работы сил поля 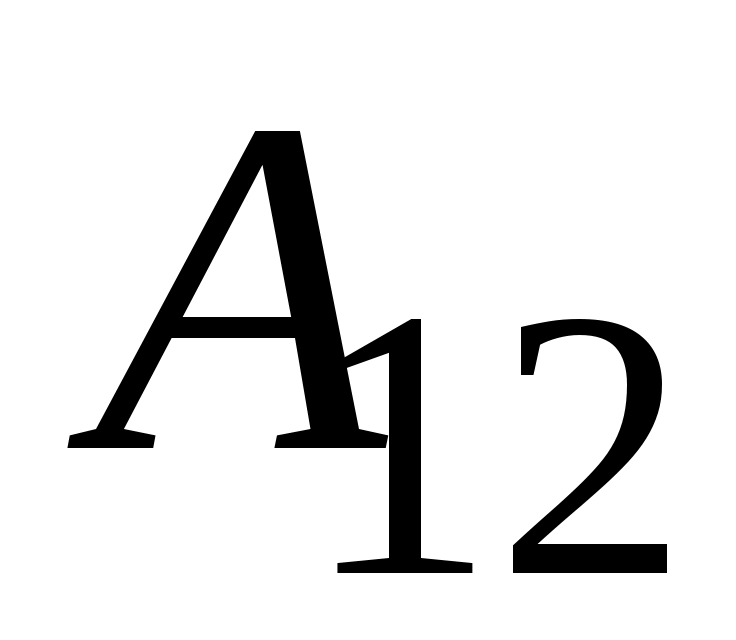 к величине заряда
к величине заряда 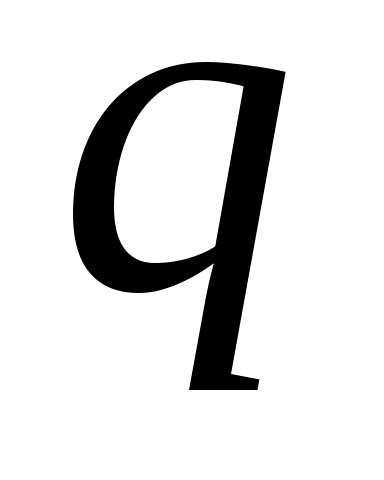
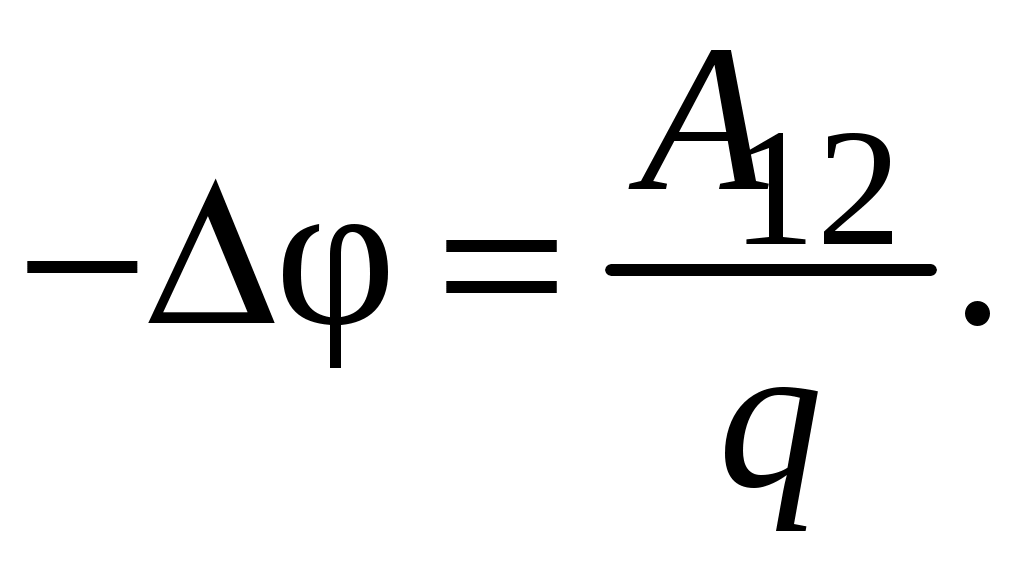 (3.5)
(3.5)
При бесконечно малом перемещении 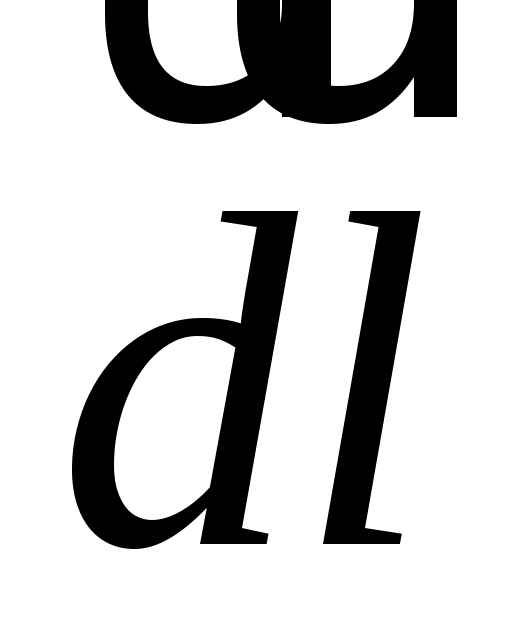 заряда
заряда 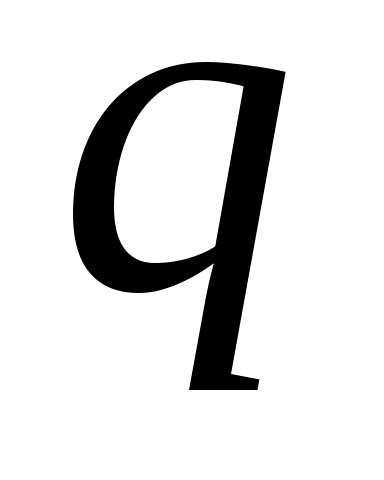 под действием силы
под действием силы 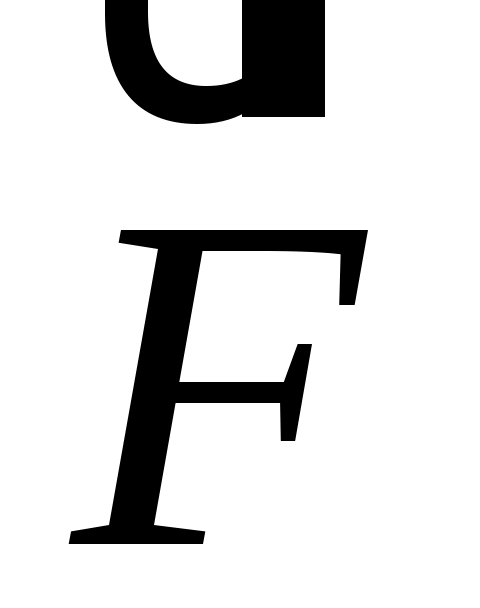 в произвольном направлении совершается элементарная работа
в произвольном направлении совершается элементарная работа 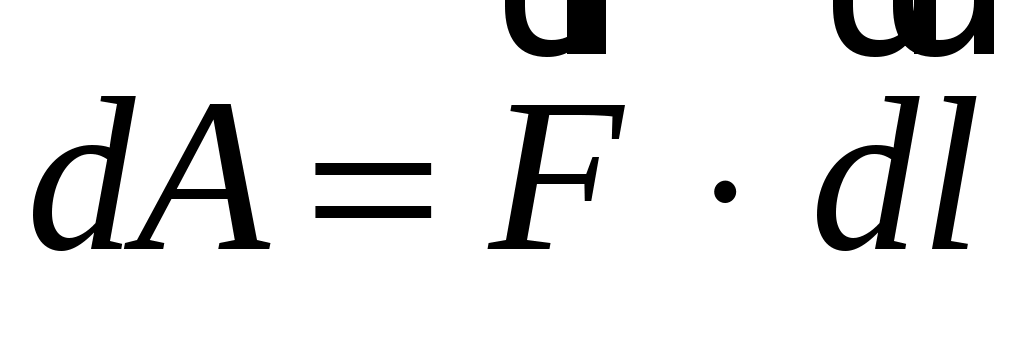 . Тогда из (3.5), с учетом (3.3), получим, что для электростатического поля малая разность потенциалов связана с напряженностью выражением
. Тогда из (3.5), с учетом (3.3), получим, что для электростатического поля малая разность потенциалов связана с напряженностью выражением
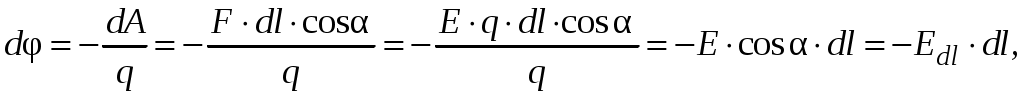 (3.6)
(3.6)
где 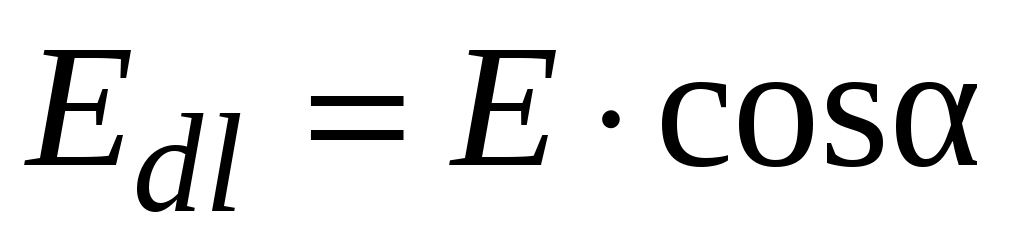 – проекция вектора
– проекция вектора 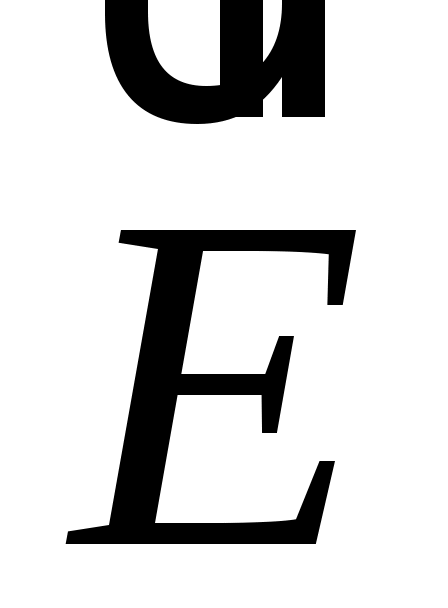 на перемещение
на перемещение 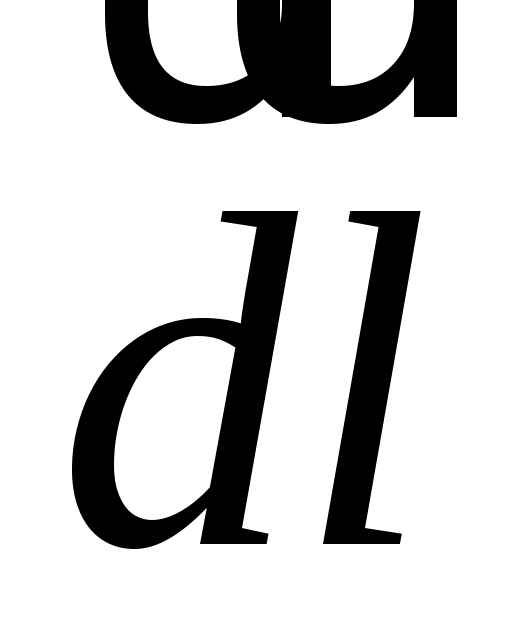 .
.
Следовательно,
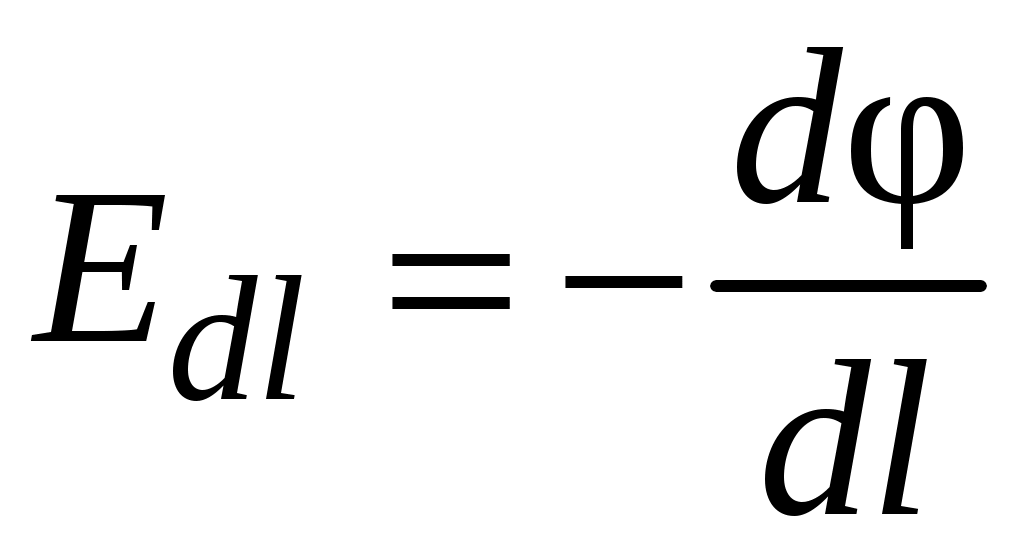 . (3.7)
. (3.7)
В декартовой системе вектор напряженности электростатического поля может быть выражен через свои проекции Ex, Ey, Ez на оси 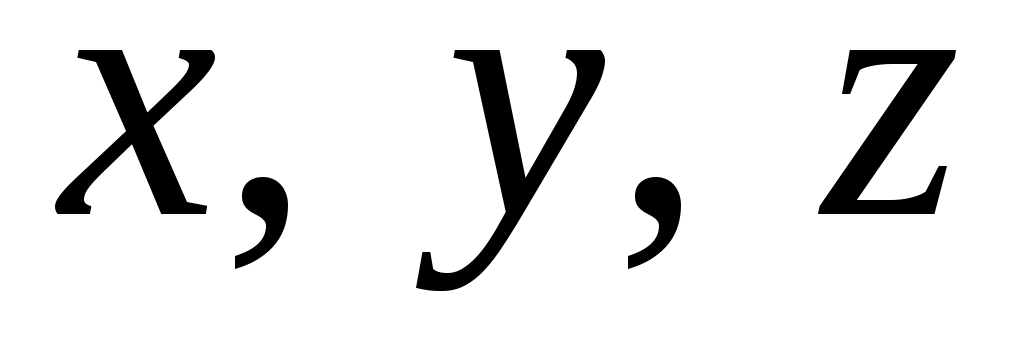 соответственно:
соответственно:
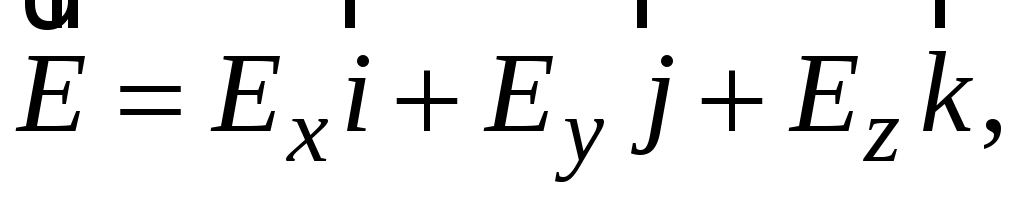 (3.8)
(3.8)
где  – орты координатных осей.
– орты координатных осей.
Из математического определения частной производной функции многих переменных, применительно к функции 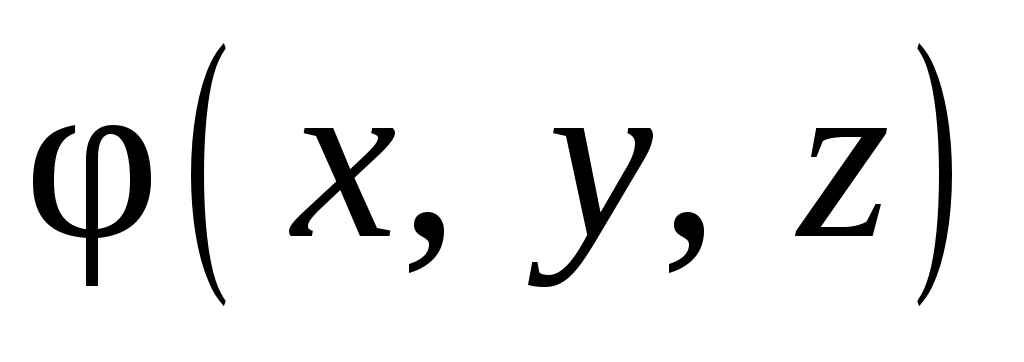 и уравнения (3.7) следует
и уравнения (3.7) следует
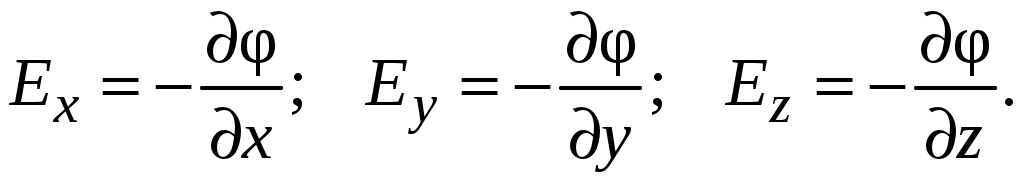 (3.9)
(3.9)
Это означает, что напряженность электростатического поля в любой точке может быть выражена через градиент потенциала в этой точке:
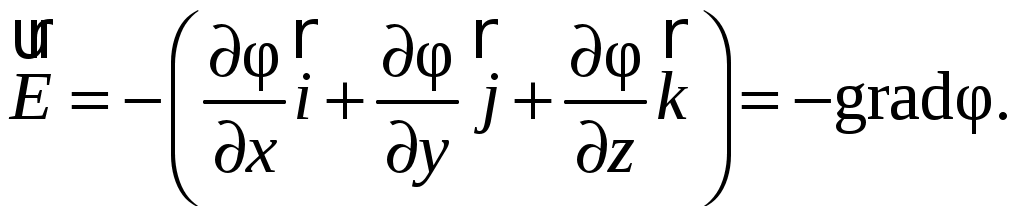 (3.10)
(3.10)
Напомним, что градиентом функции в векторной алгебре называется вектор, проекции которого на координатные оси равны частным производным от данной функции по соответствующим координатам. Градиент функции направлен в сторону ее наиболее быстрого возрастания, поэтому формула (3.10) показывает, что вектор напряженности направлен в сторону максимального убывания потенциала.
Поверхности равного потенциала 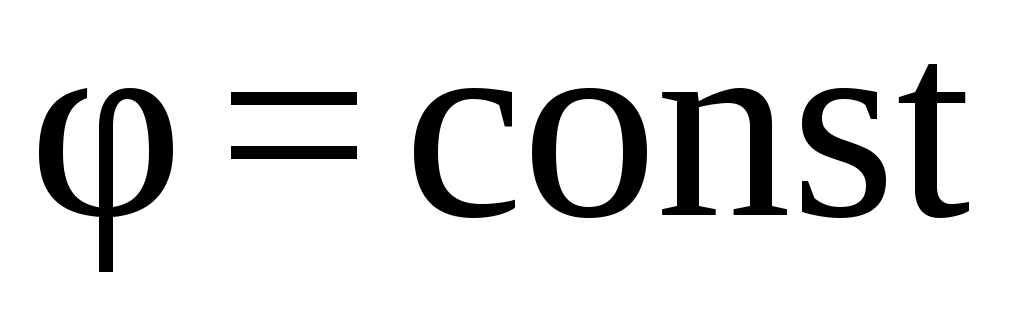 называются эквипотенциальными. Из соотношения (3.6) следует, что при перемещении заряда вдоль эквипотенциальной поверхности (d = 0) работа электростатического поля равна нулю, и это возможно только в том случае, когда вектор напряженности
называются эквипотенциальными. Из соотношения (3.6) следует, что при перемещении заряда вдоль эквипотенциальной поверхности (d = 0) работа электростатического поля равна нулю, и это возможно только в том случае, когда вектор напряженности  перпендикулярен этой поверхности (cos = 0). Следовательно, силовые линии электростатического поля пересекают эквипотенциальные поверхности под прямым углом (рис. 3.1).
перпендикулярен этой поверхности (cos = 0). Следовательно, силовые линии электростатического поля пересекают эквипотенциальные поверхности под прямым углом (рис. 3.1).
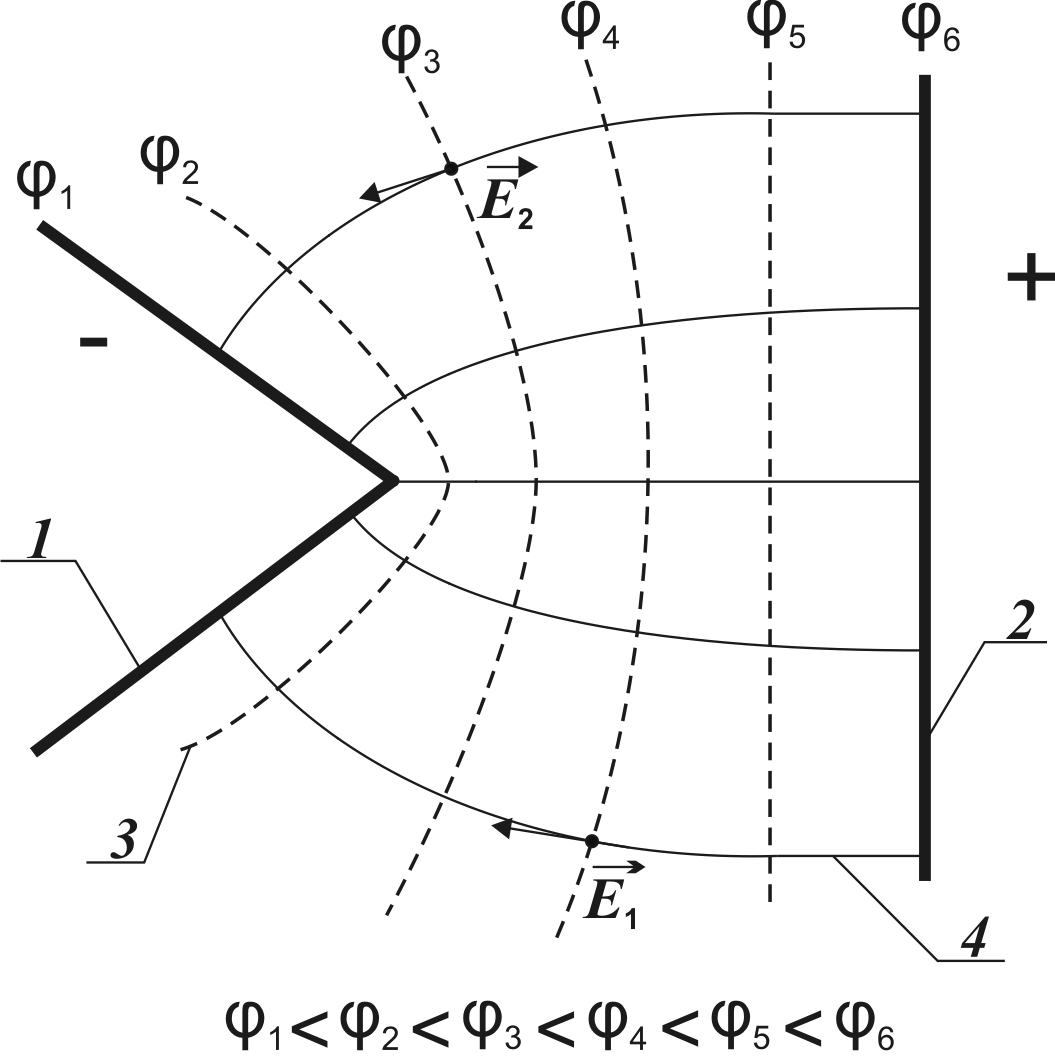
Рис. 3.1. Взаимное расположение в пространстве силовых линий
и эквипотенциальных поверхностей:
1, 2 – проводники; 3 – эквипотенциальная поверхность;
4 – линия напряженности
Внутри проводника всегда имеются свободные заряженные частицы, поэтому при внесении проводника во внешнее электростатическое поле свободные положительные заряды 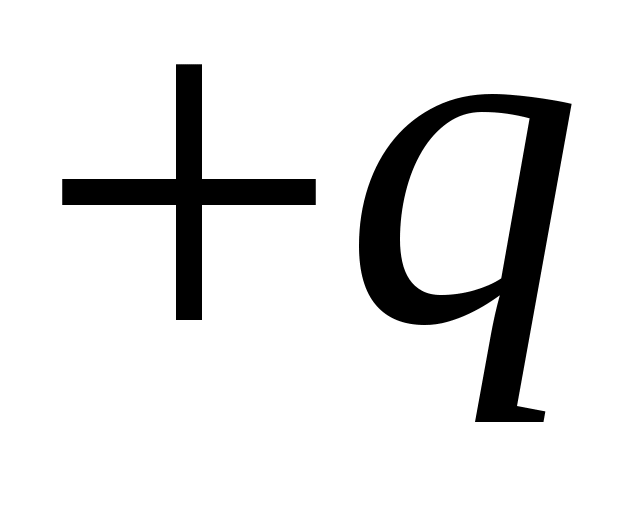 начинают двигаться в направлении вектора
начинают двигаться в направлении вектора 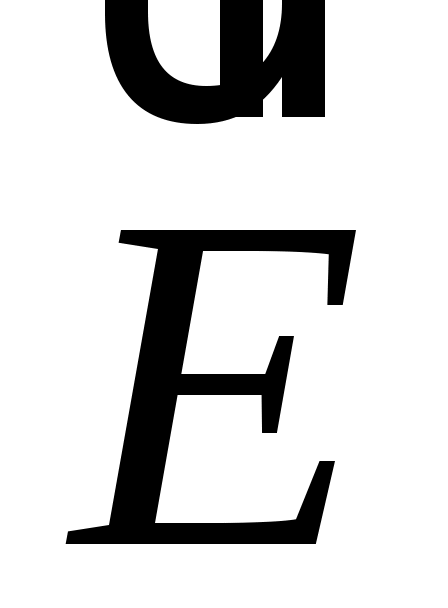 , а отрицательные – в противоположную сторону, на поверхности проводника образуются так называемые индуцированные заряды. Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов на проводнике будет происходить до тех пор, пока не будут выполнены следующие условия:
, а отрицательные – в противоположную сторону, на поверхности проводника образуются так называемые индуцированные заряды. Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов на проводнике будет происходить до тех пор, пока не будут выполнены следующие условия:
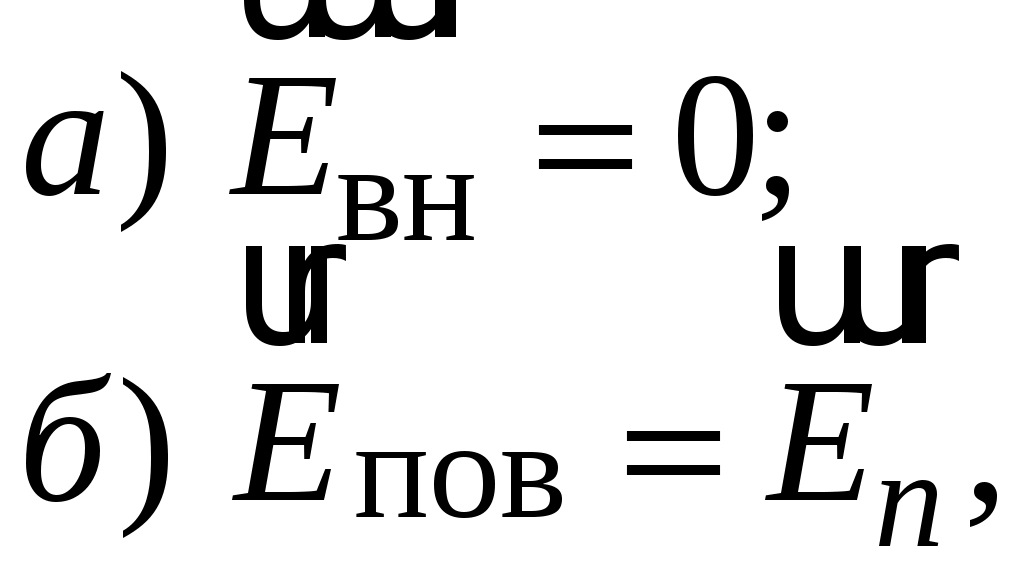 (3.11)
(3.11)
то есть: а) напряженность электрического поля внутри проводника равна 0; б) на поверхности проводника существует только нормальная составляющая электрического поля 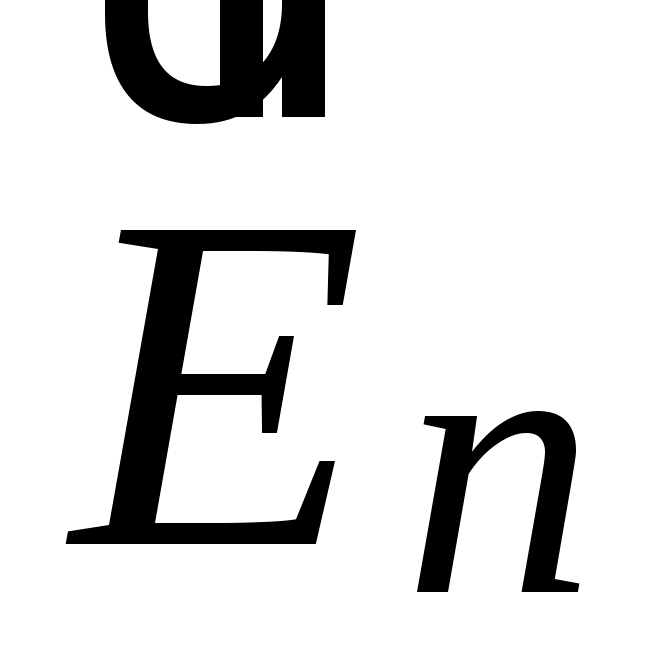 . Следовательно, поверхность проводника является эквипотенциальной и линии напряженности внешнего электрического поля перпендикулярны этой поверхности (см. рис. 3.1).
. Следовательно, поверхность проводника является эквипотенциальной и линии напряженности внешнего электрического поля перпендикулярны этой поверхности (см. рис. 3.1).
Электрическое поле, напряженность которого одинакова во всех точках:
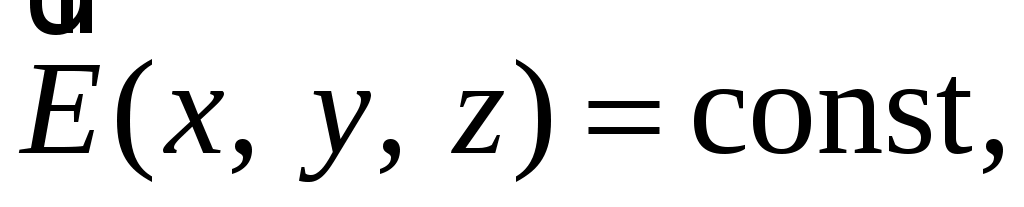
называют однородным. Очевидно, что линии напряженности такого поля представляют собой параллельные прямые. Соответственно, эквипотенциальными поверхностями будут перпендикулярные к ним параллельные плоскости. Однородное поле возникает, например, между двумя параллельными плоскими заряженными проводниками, размеры которых велики по сравнению с расстоянием между ними (рис. 3.2). Напомним, что такая система проводников называется плоским конденсатором.
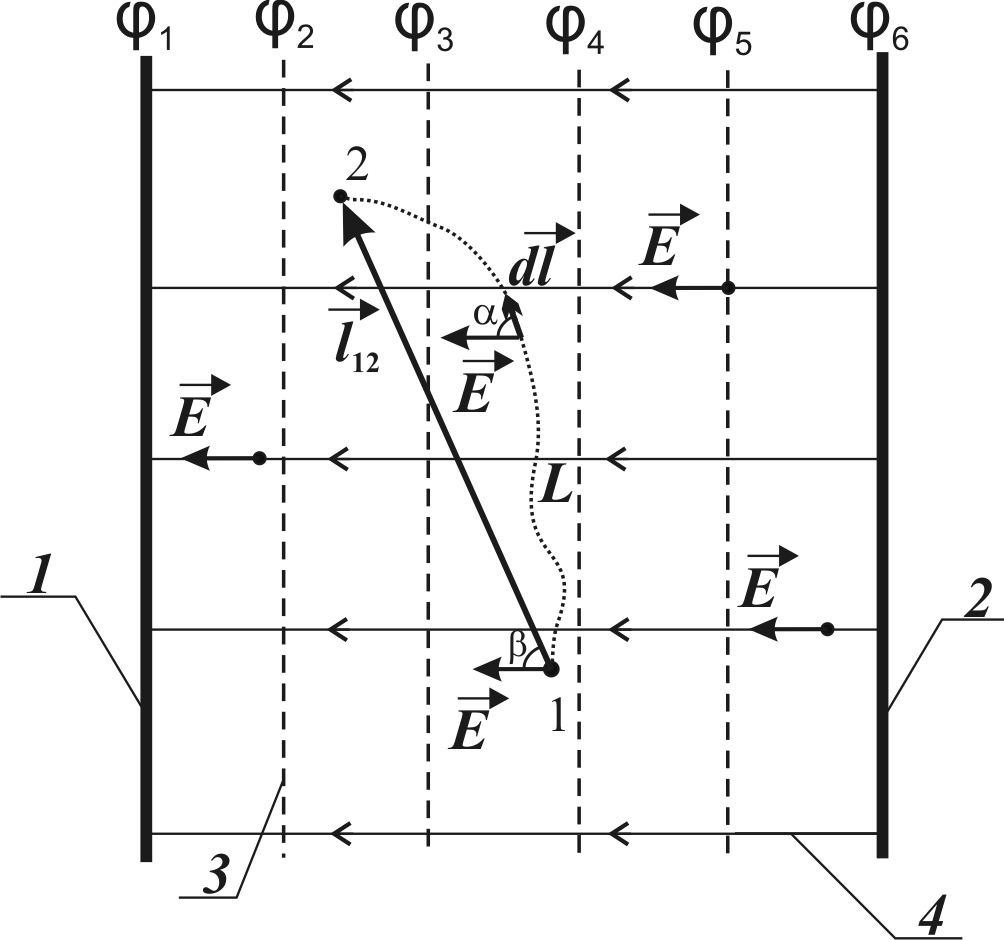
Рис. 3.2. Однородное электрическое поле:
1, 2 – параллельные проводники; 3 – эквипотенциальная
поверхность; 4 – линия напряженности
В однородном поле очень легко проинтегрировать уравнение (3.6), чтобы получить разность потенциалов между любыми двумя точками 1 и 2. Если учесть, что постоянный вектор напряженности 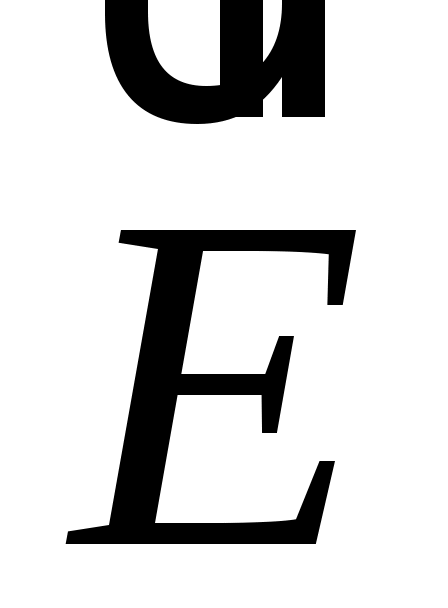 можно вынести за знак интеграла, как любой постоянный множитель, то, интегрируя по произвольному пути L (см. рис. 3.2), получим:
можно вынести за знак интеграла, как любой постоянный множитель, то, интегрируя по произвольному пути L (см. рис. 3.2), получим:
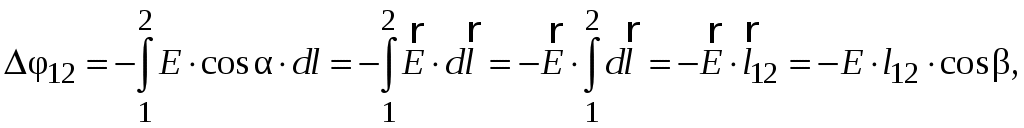 (3.12)
(3.12)
где 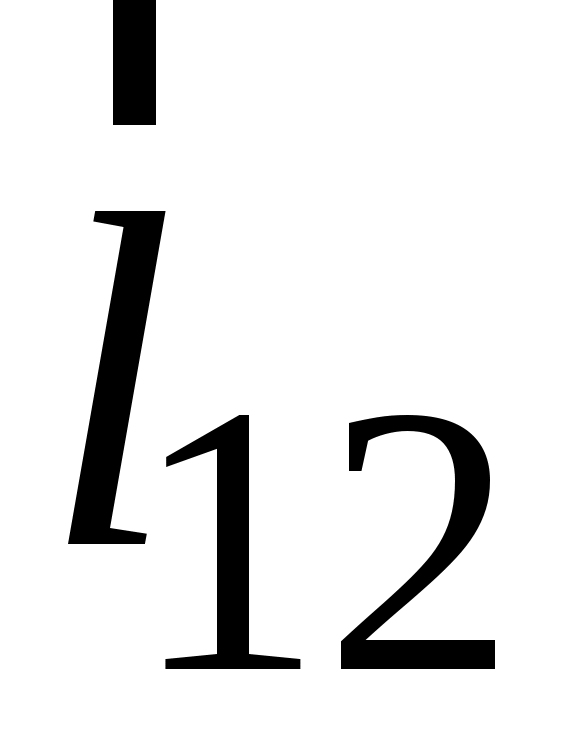 – вектор, проведенный от точки 1 к точке 2;
– вектор, проведенный от точки 1 к точке 2;
– угол между векторами 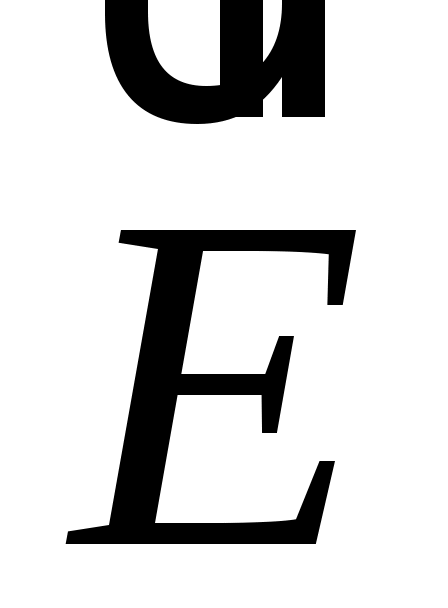 и
и 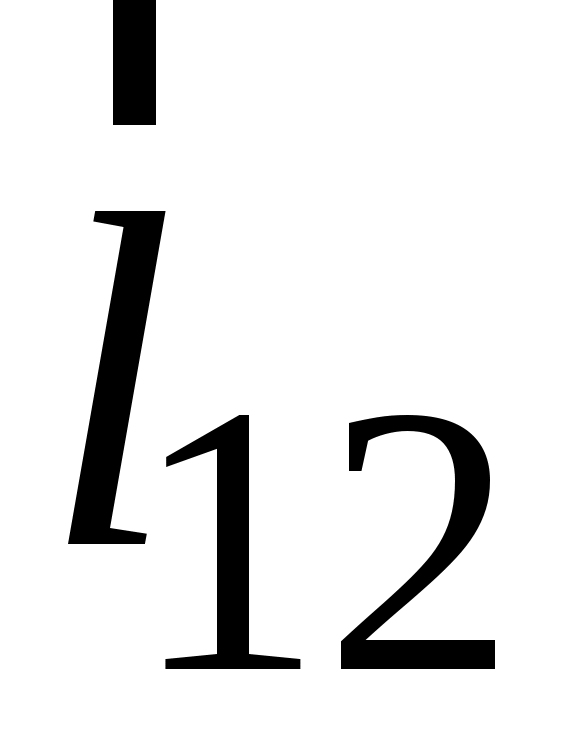 .
.
Если точки 1 и 2 лежат на одной линии напряженности, то есть векторы 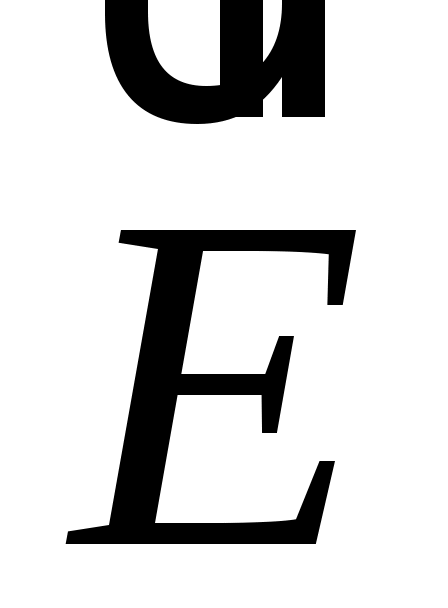 и
и 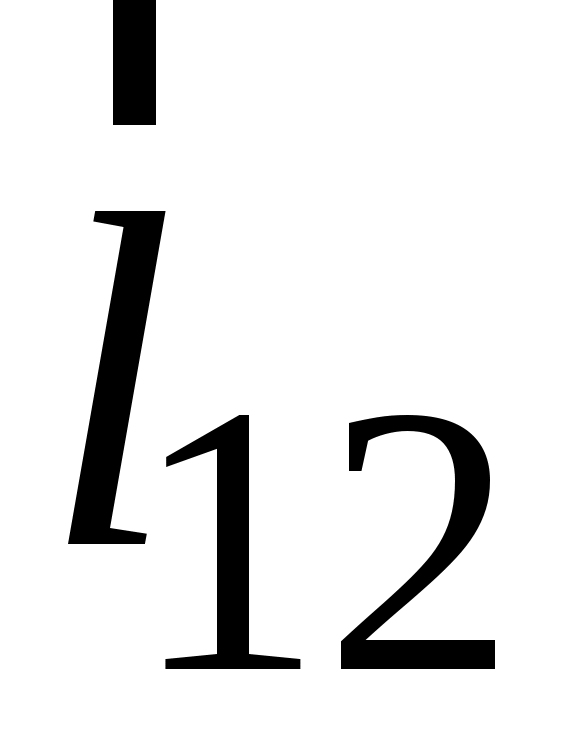 параллельны, то угол = 0 или 180°, и формула (3.12) превращается в
параллельны, то угол = 0 или 180°, и формула (3.12) превращается в
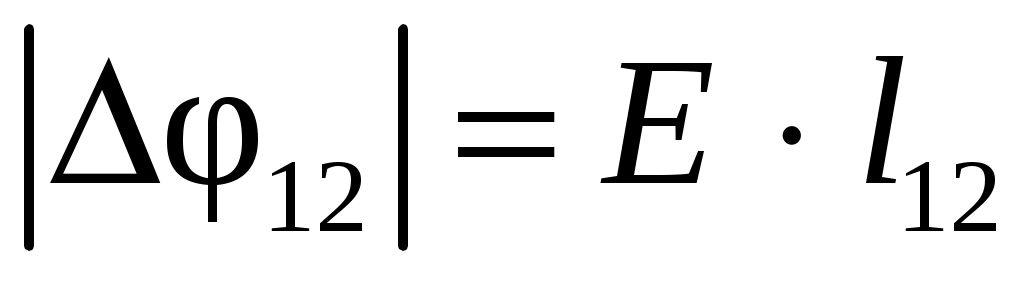 . (3.13)
. (3.13)
Эта формула позволяет приближенно вычислить напряженность электрического поля в точке, в окрестности которой оно мало отличается от однородного. Достаточно провести через данную точку линию напряженности и измерить вдоль нее расстояние 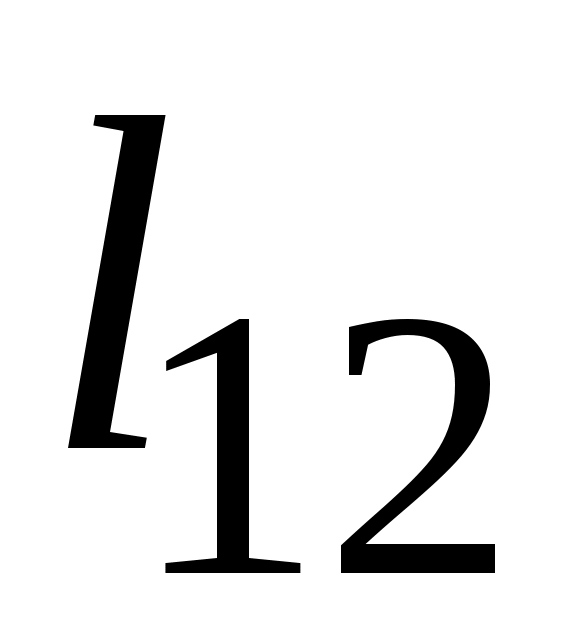 между ближайшими эквипотенциальными поверхностями с потенциалами 1 и 2, после чего найти величину напряженности по формуле
между ближайшими эквипотенциальными поверхностями с потенциалами 1 и 2, после чего найти величину напряженности по формуле
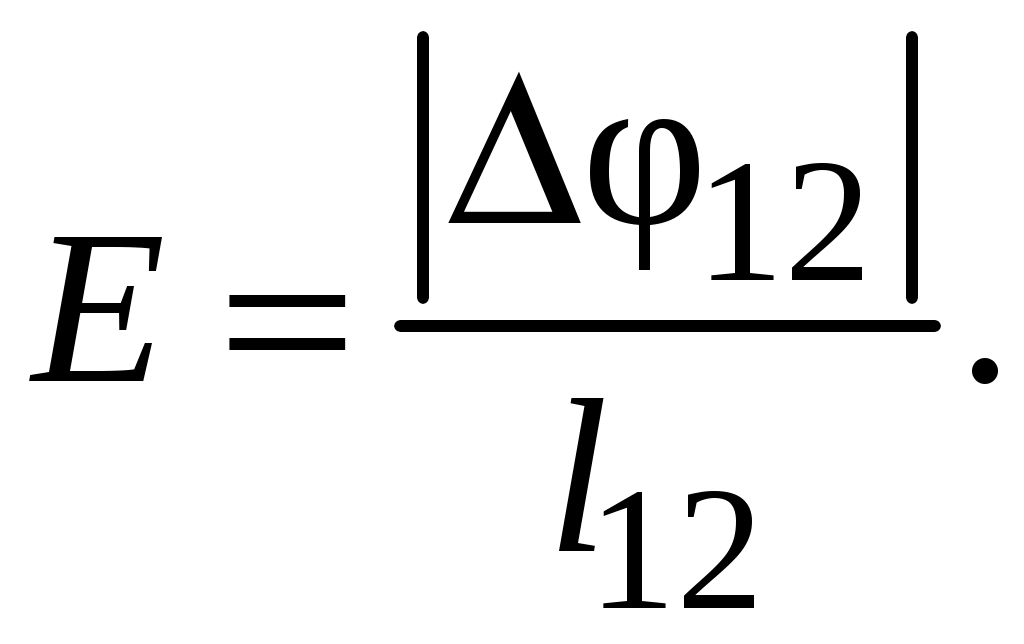 (3.14)
(3.14)
Экспериментальная установка
Изучение электростатического поля состоит в определении величины и направления вектора напряженности 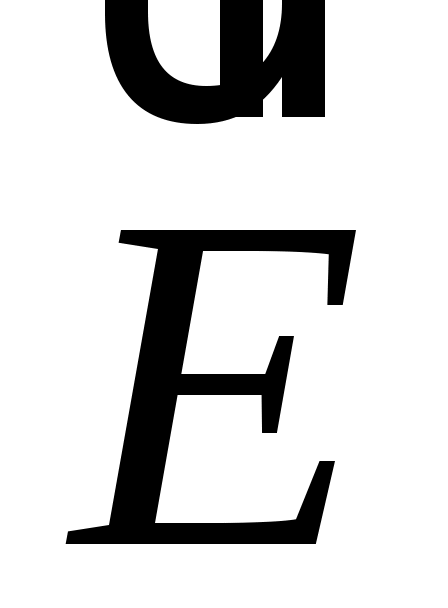 . Но на практике гораздо проще исследовать пространственное распределение потенциалов
. Но на практике гораздо проще исследовать пространственное распределение потенциалов 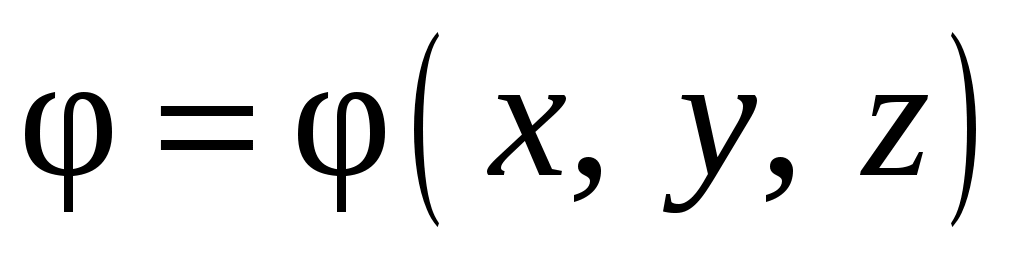 , построить картину эквипотенциальных поверхностей, и, используя взаимную перпендикулярность линий напряженности и эквипотенциальных поверхностей, воссоздать картину силовых линий электростатического поля.
, построить картину эквипотенциальных поверхностей, и, используя взаимную перпендикулярность линий напряженности и эквипотенциальных поверхностей, воссоздать картину силовых линий электростатического поля.
В данной лабораторной работе (рис. 3.3) исследуется квазистационарное электрическое поле, которое возникает в слабопроводящей среде (водопроводная вода), в которую помещены электроды – металлические проводники, подсоединенные к источнику переменного напряжения. Так как проводимость такой среды намного меньше проводимости проводника, то поверхность проводника с большой степенью точности можно считать эквипотенциальной, при этом топография поля в пространстве между электродами будет аналогична топографии электростатического поля заряженных проводников в непроводящей среде. Известно, что водопроводная вода содержит в небольших количествах молекулы солей металлов, которые в электрическом поле распадаются на ионы металлов и ионы оснований, и, в дальнейшем, могут выделяться в виде осадка вблизи электродов. Для исключения такого электролиза используется переменное напряжение U
с частотой 50 Гц. В этом случае внутри электролитической ванны, между электродами, возникает квазистационарное электрическое поле с распределением потенциалов, аналогичным случаю электростатического поля неподвижных заряженных тел. Токи, возникающие в слабопроводящей среде, тоже являются переменными, и мы измеряем действующее значение этих токов.
экспериментально исследовать квазистационарное электрическое поле, построить картину эквипотенциальных поверхностей и линий напряженности этого поля;
определить значение модуля напряженности электрического поля в указанных точках.
электролитическая ванна;
источник переменного напряжения;
потенциометр с зондом.
закон Кулона;
понятие электрического поля;
напряженность электрического поля, линии напряженности;
потенциал электрического поля, эквипотенциальные линии;
связь между напряженностью поля и потенциалом.
Что называется напряженностью электрического поля?
Что такое силовая линия электрического поля?
Что называется потенциалом электростатического поля?
Как расположены друг относительно друга в пространстве линии напряженности и эквипотенциальные поверхности?
Как связаны между собой напряженность и потенциал в данной точке?
Каковы условия равновесия зарядов на проводнике в электростатическом поле?
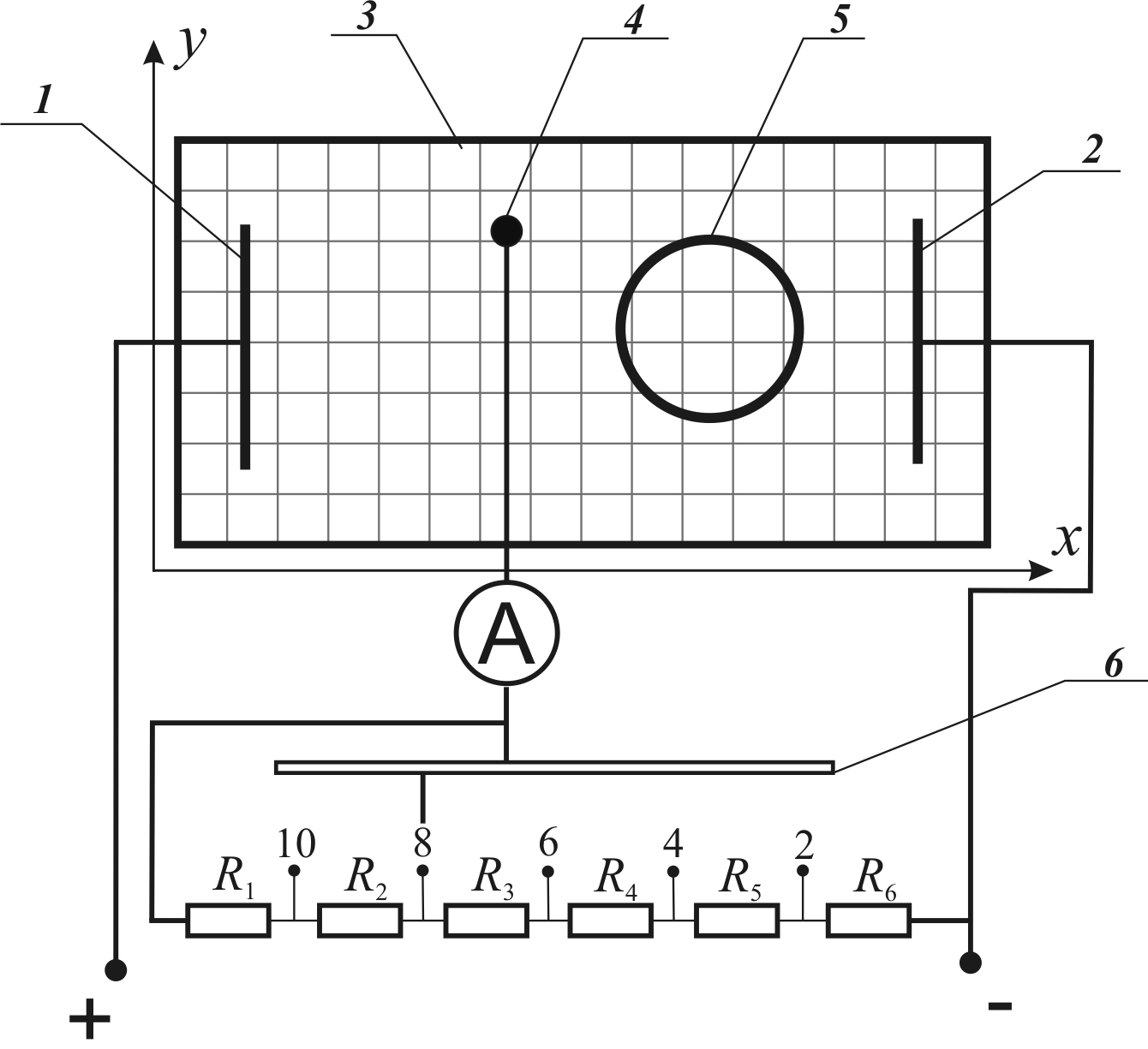
Рис. 3.3. Схема лабораторной установки для исследования
электростатического поля:
1, 2 – электроды; 3 – электролитическая ванна; 4 – зонд; 5 – металлическое
тело; 6 – переключатель потенциометра
Порядок выполнения лабораторной работы
-
Согласуйте с преподавателем расположение электродов в электролитической ванне и подключите электроды к разъемам лабораторной установки. -
Налейте воду в электролитическую ванну и включите установку в сеть переменного напряжения. -
Начертите на тетрадном листе в клетку схему расположения электродов в масштабе, точно воспроизведя при этом координатную сетку, имеющуюся на дне ванны. -
Переключатель потенциометра установите в положение «2 В» и опустите зонд в электролитическую ванну. Во всех точках с тем же потенциалом показание амперметра, включенного последовательно, будет минимально. С помощью зонда необходимо определить положение нескольких (8–10) точек указанного потенциала и координаты этих точек перенести на схему. -
Переведите переключатель потенциометра в последующие положения «4В, 6В,…» и определите координаты точек других потенциалов. -
Постройте картину эквипотенциальных линий, соединив на схеме точки одинаковых потенциалов. -
Используя свойство взаимной перпендикулярности линий напряженности и эквипотенциальных линий, постройте картину силовых линий электрического поля с указанием направления вектора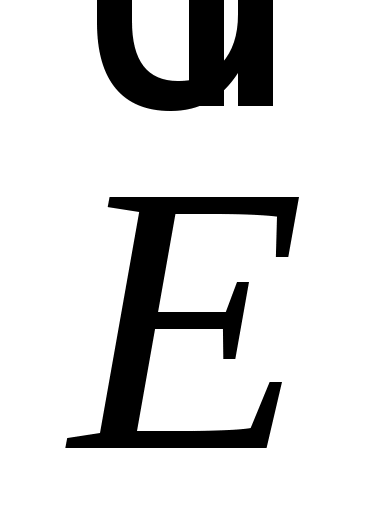 .
. -
По требованию преподавателя поместите между электродами предложенное им металлическое тело и повторите пункты 3–7, сделав чертеж на новом листе. Сравните результаты с предыдущим опытом. -
Определите значение модуля вектора напряженности электрического поля в указанных преподавателем точках.
Контрольные вопросы
-
Если известно, что напряженность электрического поля в какой либо точке равна нулю, значит ли это, что потенциал в этой точке равен нулю? -
Почему при внесении незаряженного проводника в электрическое поле изменяется картина силовых линий? -
В чем заключается метод моделирования электрического поля в среде со слабым электролитом? -
Куда направлена действующая на ионы кулоновская сила внутри ванны с электролитом? Покажите на схеме с указанными силовыми линиями.
Список литературы
-
Тюшев А. Н., Вайсберг А. И. Курс лекций по физике : учеб. пособие. Ч. 2. Электричество и магнетизм. – Новосибирск : СГГА, 2011. – С. 10–39. -
Трофимова Т. И. Курс физики : учеб. пособие. – М. : Академия, 2015. – Гл. 11. -
Савельев И. В. Курс общей физики. В 3 т. Том 2. Электричество и магнетизм. Волны. Оптика [Электронный ресурс] : учеб. пособие. – СПб. : Лань, 2016. – 500 с. – Режим доступа : http://e.lanbook.com/books/element. php?pl1_id=71761 - §§1-9, 18.
4. Лабораторная работа № 22