Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл (3,25Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 153

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Погрешность методов Ньютона-Котеса

Рассмотрим один из возможных способов оценки погрешности методов численного интегрирования на примере метода средних прямоугольников.

^Дл^я^это^г^о^з^а^пи^ш^ем^вы^р^а^ж^е^ние^д^л^я^ин^те^г^р^ала^на^отре^з^кеx_i_₁, x_i^,^по^л^у^че^н^н^о^е

методом средних прямоугольников для постоянного шага интегрирования:

i
x

_fxdx hfx_i R_i,

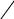^xi1

i
где

_x_x_i_₁ x_i _,_а

R_i^{– погрешность}^{интегрирования, откуда}

R_i

x

i

2
_fxdx hfx_i. (3.10)

^xi1

^{Для оценки погрешности интегрирования}R_i^{разложим}

^{подынтегральную}^{функцию}fx ^в^ряд^{Тейлора}^в^{окрестности}^{средней}^точки

x_i^:

x x²

fx 

fx_i  x  x_i f^x_i ⁱ

2

f^x_i  ... . (3.11)

^В^малой^{окрестности}^точкиx_i

в разложении (3.11) можно ограничиться

небольшим количеством членов ряда. Поэтому, подставляя в (3.10) вместо

^{функции}fx ^{ее тейлоровское разложение (3.11), и, интегрируя его}

почленно, можно вычислить интеграл с любой наперед заданной точностью

x_i



^xi1

^f ^x^dx^^hf ^xi ^

x_i

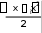^xi1

^f^ ^xi ^

x_i

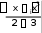^xi1

^f^ ^xi ^^...^

(*)

_h
3

^hf ^x ^

^f^ ^x ^^...

ⁱ24 ⁱ

При интегрировании и подстановке пределов получаем, что все ^{интегралы}^от^членов^ряда^(3.11),^{содержащих}^{нечетные}^{степени}^приx x_i^,

обращаются в ноль. Подставляя полученное соотношение в формулу (3.10), получим:


_h3

R_if

24

^x_i

...

При малой величине шага интегрирования h основной вклад в погрешность будет вносить первое слагаемое, называемое главным членом

погрешности вычисления интеграла на отрезке x_i_₁, x_i, будем считать его

^равнымR_i^.^{Главный}^член^полной^{погрешности}^{вычисления}^{интеграла}^на

отрезке a,b

x_i_₁, x_i^:

определяется суммированием погрешностей на каждом отрезке

_n __h²n

^   ^h2 b

a

^ 

24
R₀_R_i

i1

_hf x_i

i1

24 ^^f

xdx. (3.12)

К интегралу в формуле (3.12) мы перешли, «используя» метод средних

^{прямоугольников}^для^{функции}f^x^.

Формула (3.12) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, данная оценка является априорной, так как не требует знания значения вычисляемого интеграла. Степень, в которую возводится шаг h , называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок точности. Аналогично можно получить априорные оценки погрешностей других рассмотренных ранее методов.

Оценим погрешность метода левых прямоугольников. Погрешность

^инте^г^р^и^р^о^в^а^н^и^яR_i^н^а^отре^з^кеx_i_₁, x_i ^равняе^т^ся^ра^з^нос^т^и^ме^ж^ду^точ^н^ым

^{значением}^{интеграла}^и^его^{приближенным}^{значением}hfx_i_₁^:

R_i

x_i

_f

^xi1

xdx hf

_h2

  
^xi1 ₂

f^x_i_₁.

Из полученного выражения видно, что основной член погрешности на каждом частичном отрезке имеет второй порядок. Поскольку полное число отрезков интегрирования равно n , то полная погрешность метода левых прямоугольников может быть рассчитана следующим образом:

_n __hn

^   ^hb

^ 

2
R₀_R_i

i1

_hf

i1

^xi1

_f xdx.

a

2
Результат оценки погрешности формулы правых прямоугольников будет таким же.

Погрешность формулы трапеций оценивается аналогичным образом.

Так как значение интеграла на отрезке x_i_₁, x_i вычисляется по формуле