Добавлен: 09.11.2023
Просмотров: 78
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.3. Описание формирующего этапа эксперимента
На основании вывода констатирующего этапа эксперимента и для подтверждения гипотезы исследования был проведён формирующий этап, где участие приняли 15 учащихся экспериментальной группы 3 «Б» класса. Уроки математики проводились по программе «Школа России», «Математика». Авторы: Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова С. В.
Цель формирующего этапа эксперимента: разработка системы упражнений, направленных на формирование умений учащихся обобщать. Для реализации поставленной цели учащимся предлагались упражнения; были разработаны фрагменты уроков по программному материалу.
На каждом уроке предлагались упражнения, направленные на формирование умений учащихся обобщать.
-
Тема: «Числовые выражения»
Задание 1: Учащимся предлагается определить порядок арифметических действий.
| 900 – (600 – 100) : 5 | 150 + 50 4 + 6 |
| (900 – 600) – 100 : 5 | 880 – 720 : 8 9 |
После выполнения задания учитель, подводя итог и обобщая материал, спрашивает у учеников: «Так какое арифметическое действие будет первым? Вторым? Третьим?».
Задание 2: Учащимся предлагается расставить скобки так, чтобы равенства стали верными.
| 15 + 75 – 25 : 5 = 25 | 72 : 9 8 – 1 = 0 |
После выполнения данного задания учитель подводит итог и предлагает ребятам обобщить работу: «А какими правилами вы пользовались при постановке скобок?». Дети отвечают на вопрос учителя и делают вывод, что при расстановке скобок они не только учитывали арифметические знаки, но и использовали простейшие логические операции.
-
Тема: «Уравнения»
Задание: Учащимся предлагается найти уравнения, которые решены неправильно и решить их.
| 768 – х = 700 х = 768 – 700 х = 68 | х + 10 = 190 х = 190 + 10 х = 200 | х – 380 = 100 х = 380 – 100 х = 280 |
Перед выполнением этого задания учитель может напомнить детям, что здесь им понадобится вспомнить для успешного решения уравнений. После выполнения этого упражнения дети совместно с учителем обобщают и делают вывод:
-
для того, чтобы найти неизвестное вычитаемое, нужно из разности вычесть уменьшаемое; -
для того, чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое; -
для того, чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
-
Тема: «Виды треугольников»
Задание: Учащимся предлагается выписать номера остроугольных, прямоугольных и тупоугольных треугольников (см. рис. 2.1.).
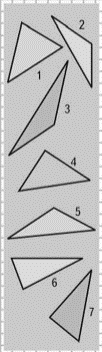
Рис. 2.1. Виды треугольников
После выполнения этого задания учитель может предложить детям начертить равнобедренный, равносторонний и разносторонний треугольники. Подводя итог, учитель задаёт детям наводящие вопросы: «Какие есть виды треугольников по их сторонам?», «Какие вы знаете виды треугольников по их углам?». И учащиеся называют способы определения треугольников по его углам и сторонам. После сделанного вывода и обобщения дети характеризуют каждый треугольник, который находится на полях учебника. Например, треугольник №1 – равнобедренный, остроугольный, треугольник №2 – разносторонний, тупоугольный и т. д.
-
Тема: «Внетабличное деление»
Задание: Учащимся нужно найти частное и остаток, используя значение первого выражения в каждом столбике. Данное упражнение даётся детям на повторение алгоритма умножения двузначного числа на однозначное.
| 84 : 12 85 : 12 94 : 12 | 76 : 4 77 : 4 79 : 4 | 69 : 23 79 : 23 90 : 23 |
Учитель спрашивает у детей последовательность действий при умножении двузначного числа на однозначное, при этом составляя алгоритм совместно с детьми. После выполнения задания учитель проверяет результаты деления у учащихся с проговариванием алгоритма вслух.
Тема: «Периметр и площадь квадрата и прямоугольника»
Задание: ученикам предлагается найти длину стороны квадрата и площадь, если периметр его равен 28 см. Учитель задаёт детям наводящие вопросы о том, что такое периметр и площадь, и как их найти. После вопросов дети выполняют задание, а в конце обобщают, что для нахождения одной стороны при периметре квадрата 28, нужно периметр квадрата разделить на количество сторон - 28 : 4 = 7, значит, сторона квадрата 7 см. Дети называют формулу нахождения площади и пользуются ею: 7 7 = 49 см
2 – площадь квадрата.
Кроме представленных выше упражнений, на каждом уроке изучения нового материала использовался приём обобщения. Ниже представлены фрагменты уроков.
Фрагмент урока № 1.
Тема урока: Вычисления вида 240 3, 960 : 3.
Цель: ознакомление учащихся с приёмами устных вычислений деления и умножения трёхзначных чисел, основанными на свойствах умножения и деления суммы на число.
Подготовительная работа.
Перед изучением новой темы учитель предлагает учащимся соотнести выражения со свойствами арифметических действий, которые они иллюстрируют (см. рис. 2.2.).
| 23 4 = 20 4 + 3 4 | | Переместительное свойство умножения |
| | | |
| 56 : 4 = 40 : 4 + 16 : 4 | | Умножение суммы на число |
| | | |
| 8 12 = 12 8 | | Деление суммы на число |
Рис. 2.2. Пример задания из учебника
Затем учитель задаёт детям обобщающие вопросы.
-
В чём суть переместительного свойства умножения? -
Как это можно применить при вычислениях? -
Объясните, в чём заключается свойство умножения суммы на число? (Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и результаты сложить.) -
А в чём заключается свойство деления суммы на число? (Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и результаты сложить.)
После обобщения свойств арифметических действий учитель предлагает учащимся рассмотреть пары выражений и ответить на вопрос: «Как математические свойства, о которых только что говорили, можно применить при умножении и делении трёхзначных чисел?»
Дети обобщают и делают вывод о том, что при умножении и делении трёхзначных чисел можно заменить умножение и деление трёхзначных чисел действиями с сотнями и десятками, число 230 – это 23 десятка, а число 560 – это 56 десятков.
Изучение нового материала.
Учащиеся наблюдают над примером 240 3. Учитель записывает у доски решение, а ученики комментируют. Число 240 нужно представить в виде суммы разрядных слагаемых: 200 и 40, а затем каждое слагаемое умножить на 3. После этого результаты умножения складываются и дети читают ответ: 240 3 = (200 + 40) 3 = 200 3 + 40 3 = 600 + 120 = 720.
Учитель записывает пример второго вида на доске 960 : 6.
-
Как заменить число 960? (Суммой удобных слагаемых – 600 и 360.)
Дети заменяют число 960 суммой удобных слагаемых и затем каждое слагаемое делят на 6. После этого результаты деления складываются и зачитывается ответ: 960 : 6 = (600 + 360) : 6 = 600 : 6 + 360 : 6 = 100 + 60 = 160.
После наблюдения над выражениями учитель просит обучающихся открыть учебник и сравнить вычисления на доске и в учебнике.
Дети отвечают, подтверждая свои предположения, что это умножение суммы на число и деление суммы на число. Учитель подводит итог и обобщает, что вычисления сделаны правильно.
Фрагмент урока № 2.
Тема урока: Виды треугольников.
Цель: формирование умения различать треугольники по видам углов.
Подготовительная работа.
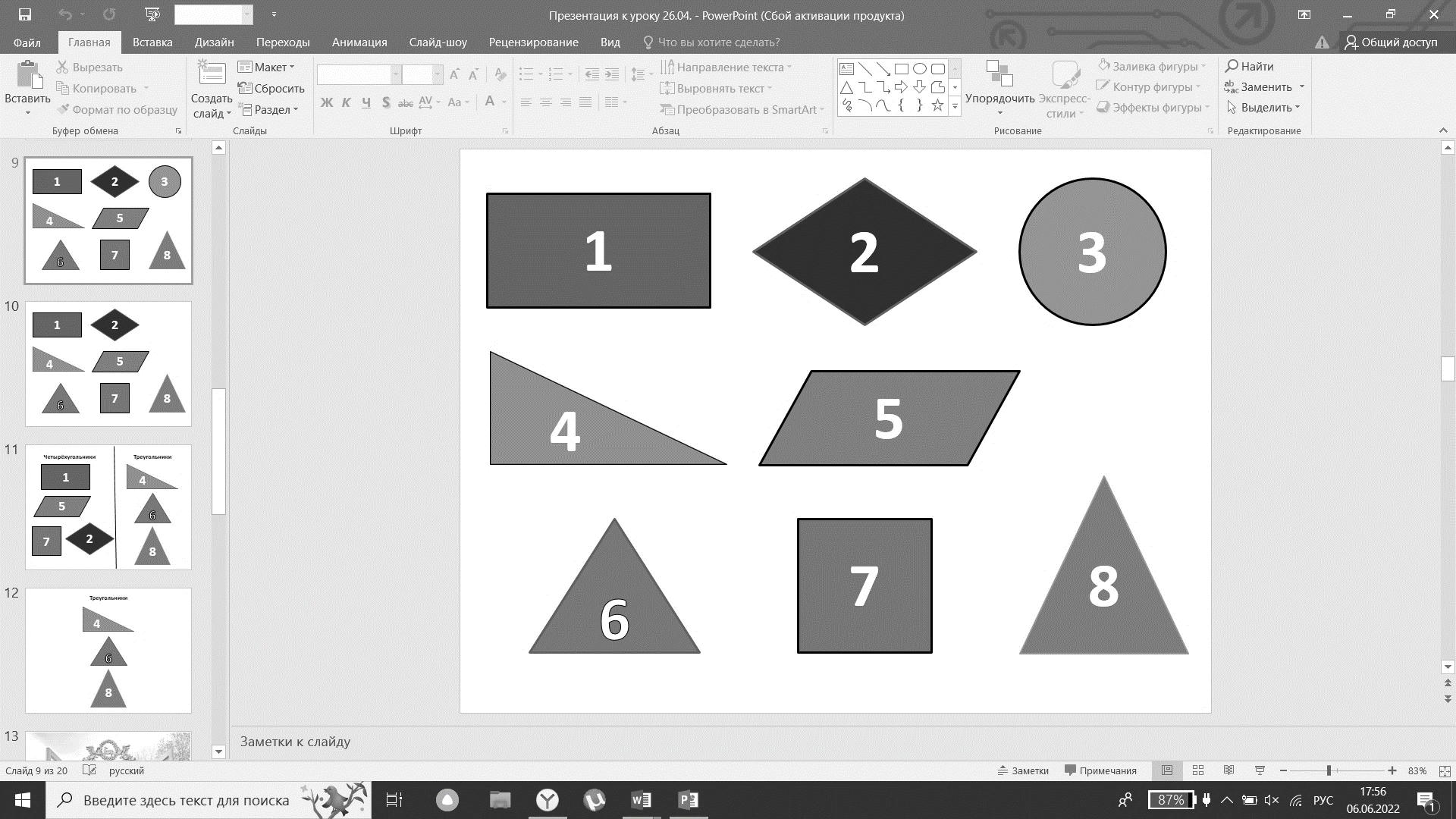
Рис. 2.3. Геометрические фигуры
-
Найдите лишнюю фигуру (см. рис. 2.3.).
Учащиеся говорят, что это фигура под №3 (круг) и объясняют это тем, что только у этой фигуры нет углов.
-
На какие группы можно разделить оставшиеся фигуры? (Четырёхугольники и треугольники).
Учитель предлагает детям объяснить причину получения треугольниками такого названия.
-
На какие группы можно разделить треугольники по длине сторон?
Дети вспоминают, что треугольники по длине сторон бывают разносторонними, равнобедренными и равносторонними, а также они отмечают, почему эти треугольники получили такое название. После этого учитель помогает вспомнить виды углов.
Затем учитель задаёт проблемный вопрос: «Есть ли такие виды треугольников, которые различаются по углам?» И тогда дети формулируют тему урока и ставят цели на урок.
Изучение нового материала:
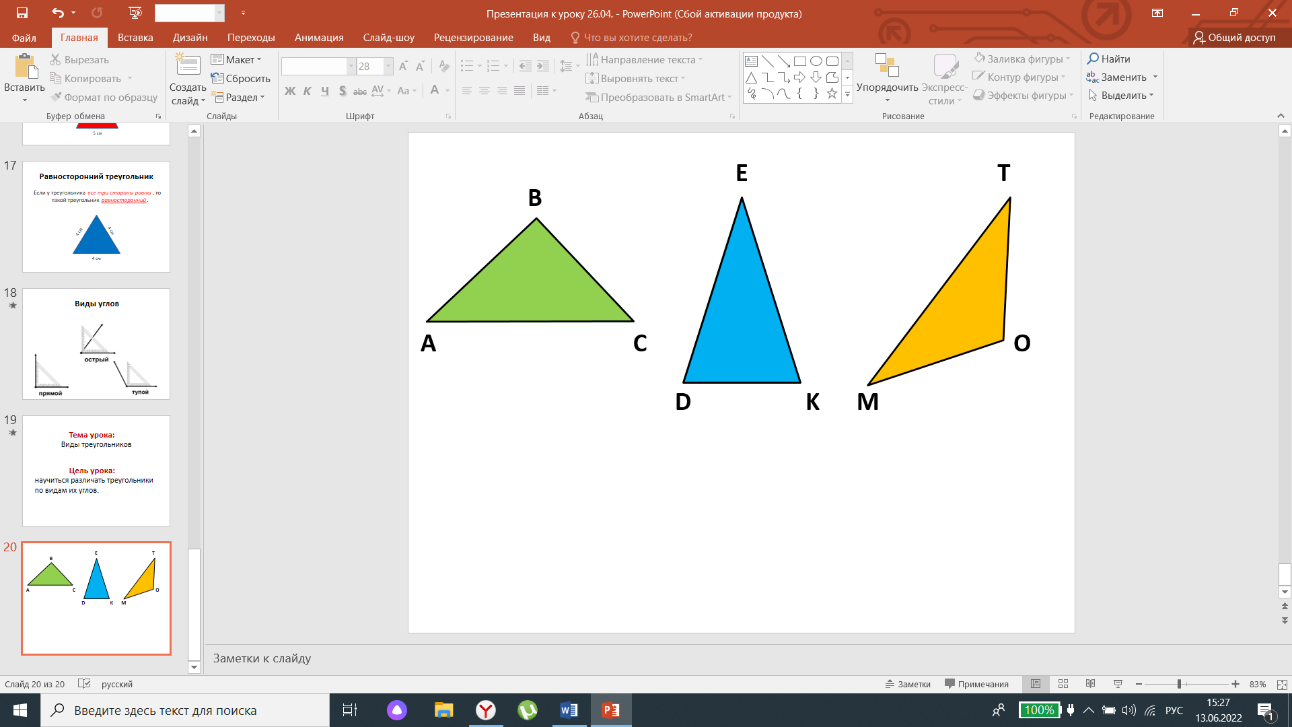
Рис. 2.3. Треугольники
На доске расположены геометрические фигуры (см. рис. 2.3.).
Учащиеся с помощью модели прямого угла (угольника) определяют виды треугольников.
-
Назовите треугольник, у которого есть острый угол. -
Назовите треугольник, который имеет тупой угол. -
У какого треугольника прямой угол?
После нахождения всех треугольников, учитель задаёт детям обобщающие вопросы: «Как можно назвать треугольник, у которого все углы острые?», «Как назвать треугольник, который имеет тупой угол? Прямой угол?»
После обобщающего вывода, который сделали дети, они открывают учебник и читают теоретический материал, в котором убеждаются, что вывод сделан правильно.
Учитель задаёт обобщающий вопрос: «С какими видами треугольников познакомились на уроке?», и далее работают по теме урока.
Фрагмент урока № 3.
Тема урока: Приёмы письменных вычислений. Алгоритм письменного умножения трёхзначного числа на однозначное.
Цель: ознакомление с алгоритмом письменного умножения трёхзначного числа на однозначное с переходом через разряд.
Подготовительная работа.
На доске записан пример, который нужно решить в столбик.
234 2
-
В каком порядке выполняли вычисления? (Сначала умножали единицы, потом десятки, потом сотни.)
Изучение нового материала.
При изучении новой темы учитель также предложил решить детям пример в столбик.
325 3
Желающий ученик выходит к доске и приступает к решению. Учитель во время решения задаёт наводящие вопросы.
-
В каком порядке вычисляли по разрядам в столбик? -
Почему в десятках получилось 7? (При умножении единиц получилось 15, единицы записали под единицами, десяток запомнили. Потом к 6 десяткам прибавили 1 десяток. Получилось 7 десятков.) -
Что нужно знать, чтобы не ошибаться в решении таких примеров? (Алгоритм умножения трёхзначного числа на однозначное.)
Затем совместно с детьми составляется алгоритм, который потом раздаётся каждому ученику на карточках. Учитель, обобщая алгоритм, задаёт вопрос: «Какой приём можно использовать, чтобы не забыть прибавить 1 в следующем разряде?». Далее продолжается работа по теме урока.
Фрагмент урока № 4.
Тема урока: Приёмы письменных вычислений. Алгоритм письменного деления трёхзначного числа на однозначное.
Цель: ознакомление учащихся с алгоритмом деления трёхзначного числа на однозначное.
Подготовительная работа.
На данном этапе при изучении новой темы детям предлагается заполнить таблицу.
Таблица 2.5
| Делимое | 18 | 76 | | 39 | 57 | | 29 | 65 | 88 |
| Делитель | 5 | | 7 | 6 | 8 | 7 | | | 9 |
| Частное | | 8 | 6 | | | 7 | | 9 | |
| Остаток | 3 | 4 | 3 | | 2 | 6 | 2 | | |