ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 154
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, присоединяемых к сечениям 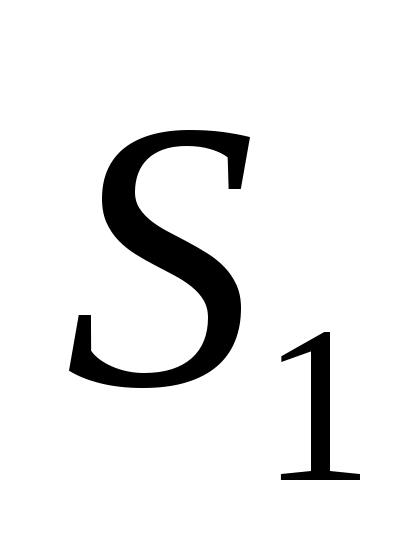 и
и 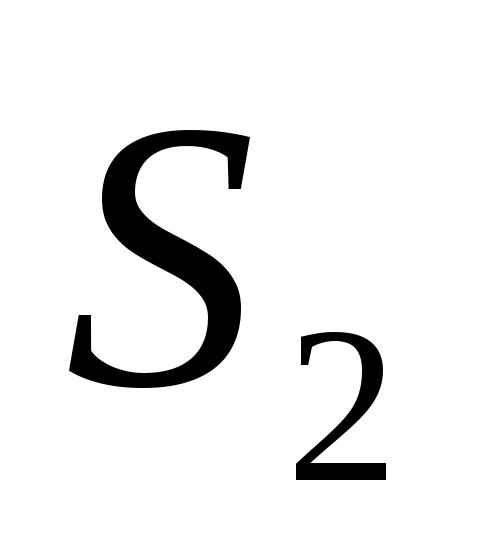 .
.
Из уравнения неразрывности следует, что скорости в сечении 1 и 2 обратно пропорциональны площадям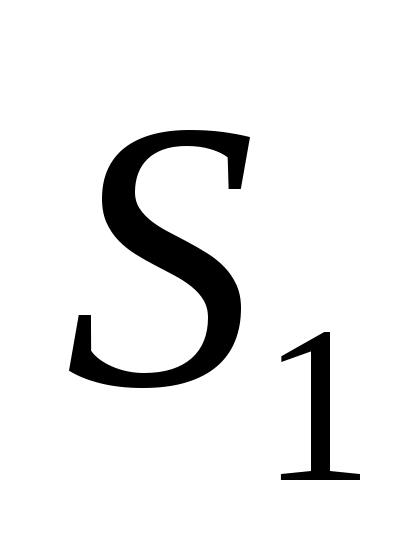 и
и 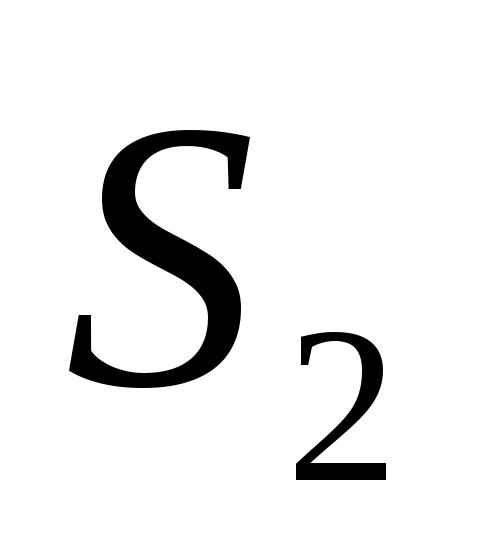 , то есть
, то есть
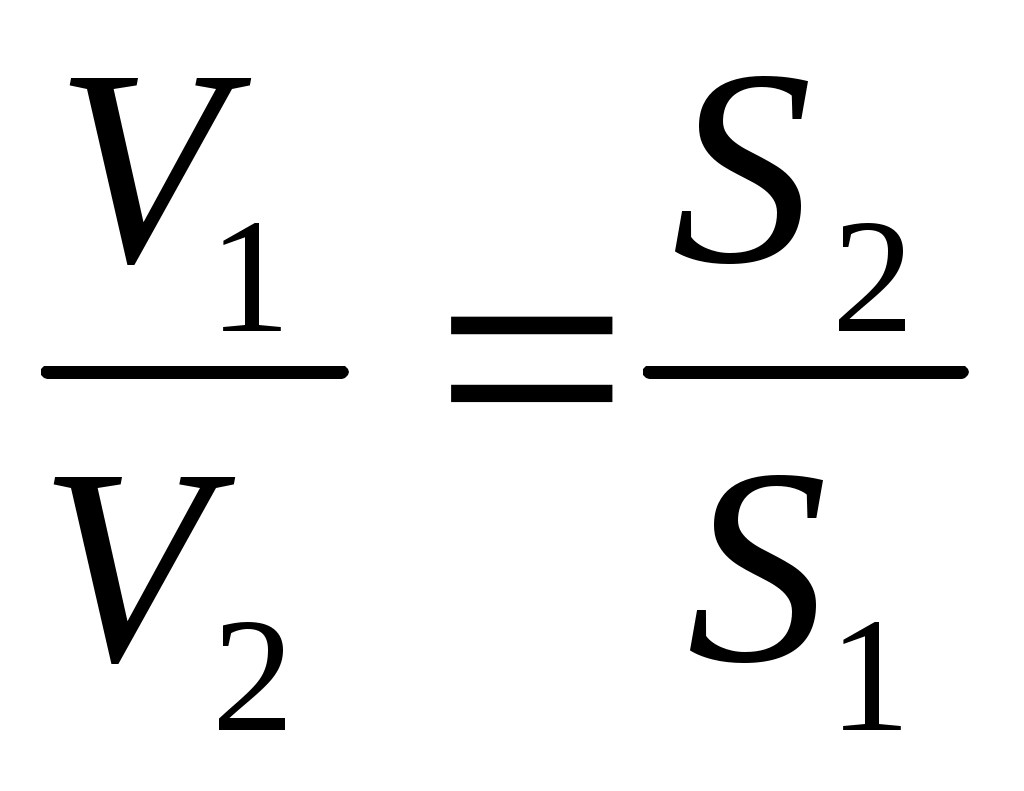 . (II.30)
. (II.30)
Представим выражение (11.30) таким образом:
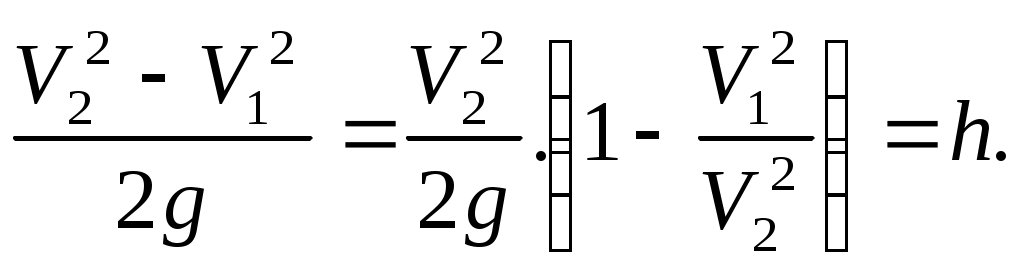 (II.31)
(II.31)
Отсюда
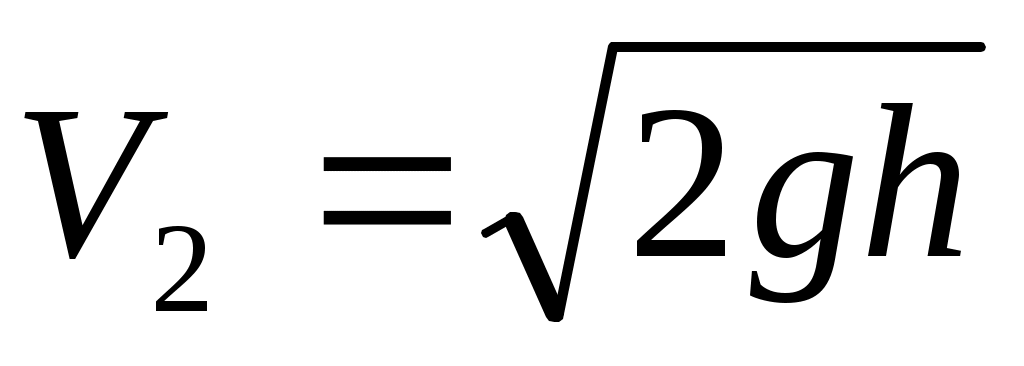
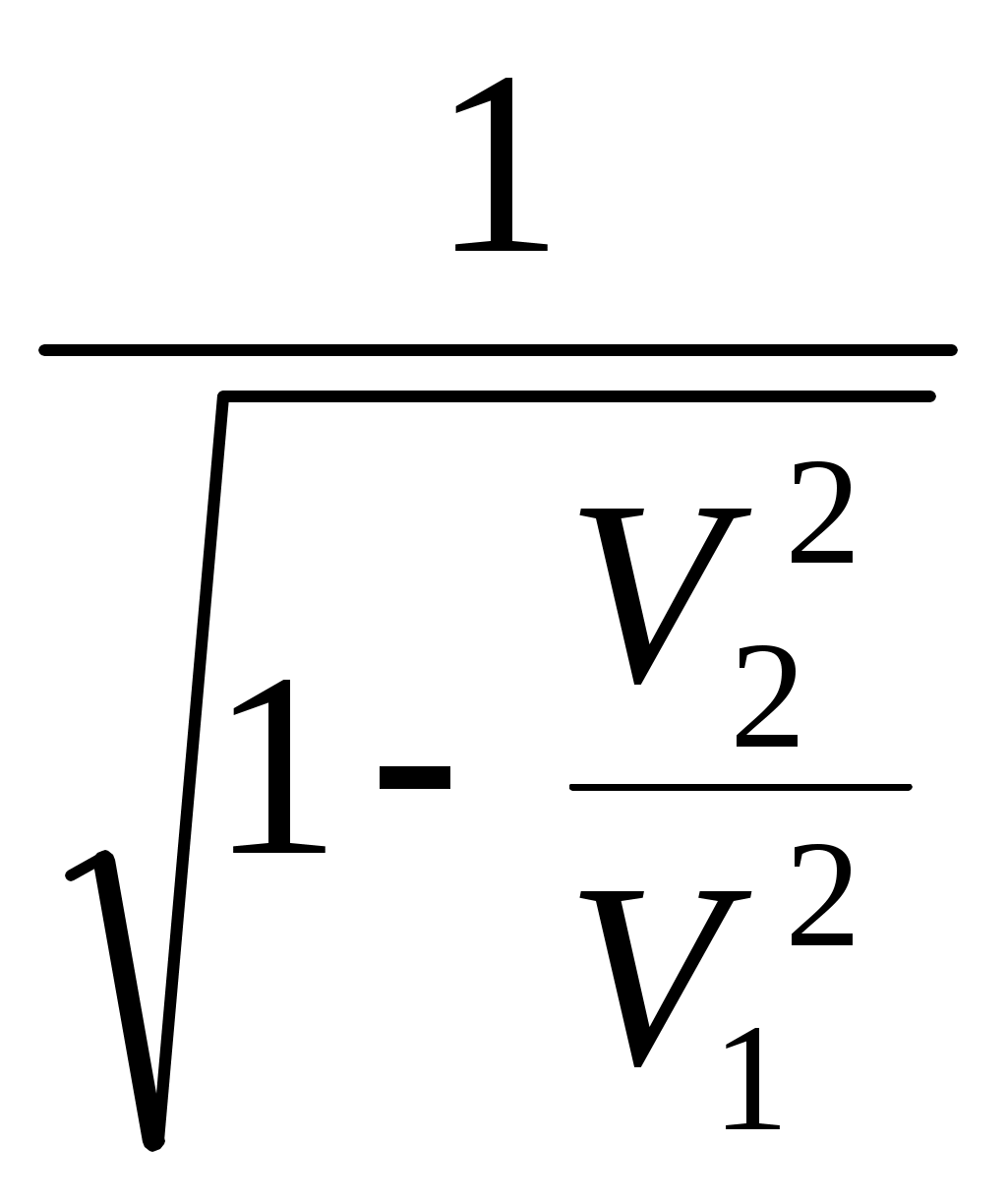
или с учетом (11.31),
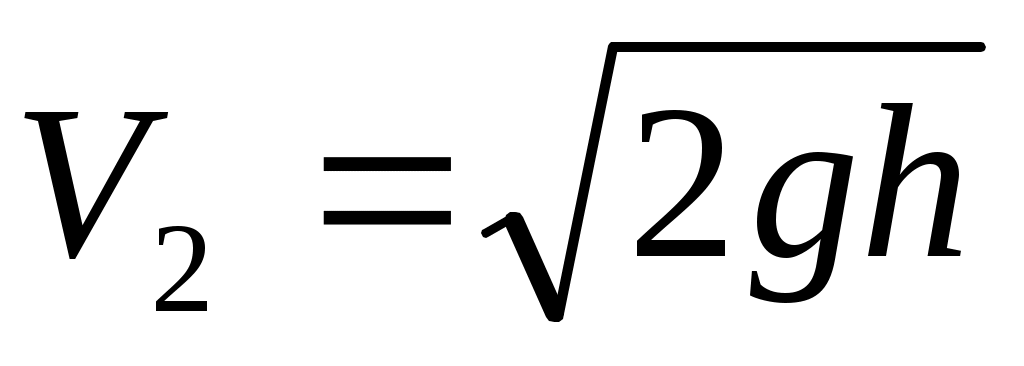
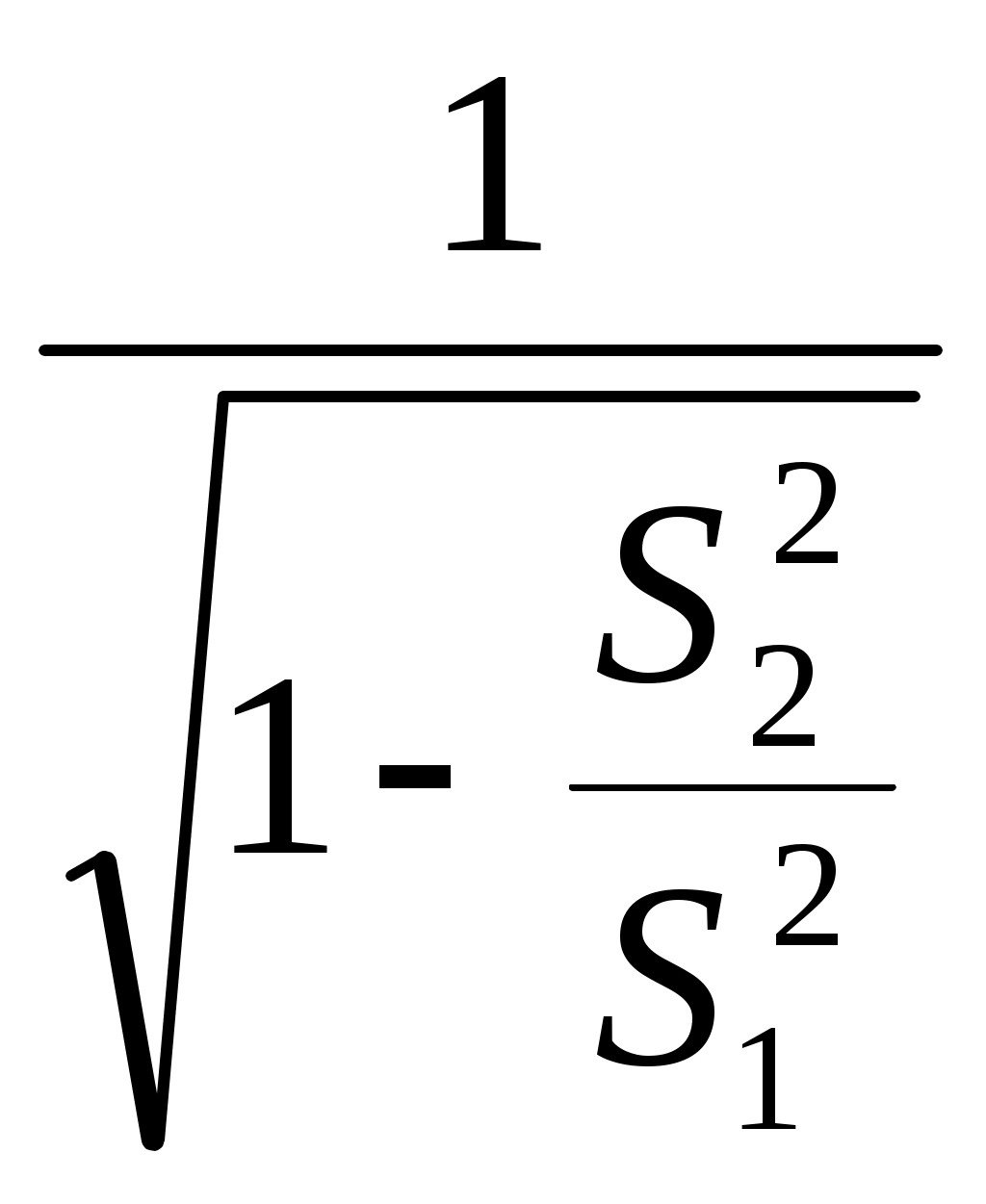
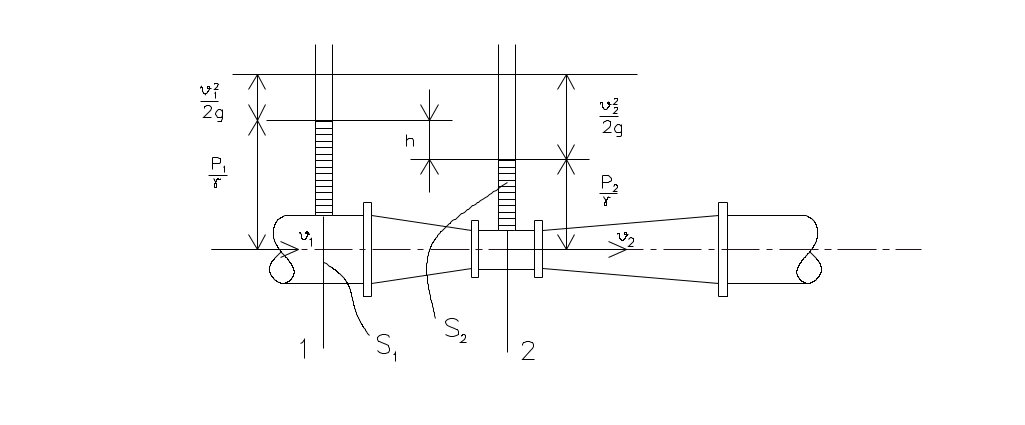
Рис. II.07.
Следовательно,
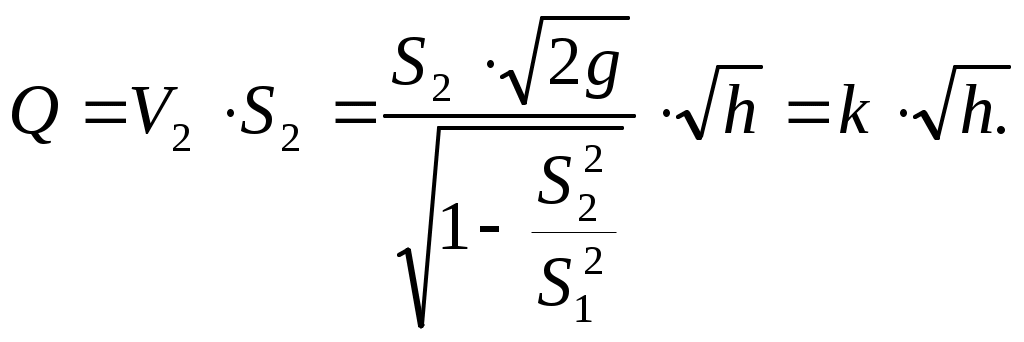 (II.32)
(II.32)
Здесь k – константа водомера, постоянная для водомера заданной конструкции и размеров.
Скорость течения жидкости может быть измерена весьма простым прибором, называемым трубкой Пито. Этот прибор представляет собой согнутую под прямым углом трубку, открытый конец которой направляется против течения так, чтобы ее ось совпала с направлением вектора скорости. Если в точке потока, в которой измеряется скорость, предварительно измерить пьезометрический напор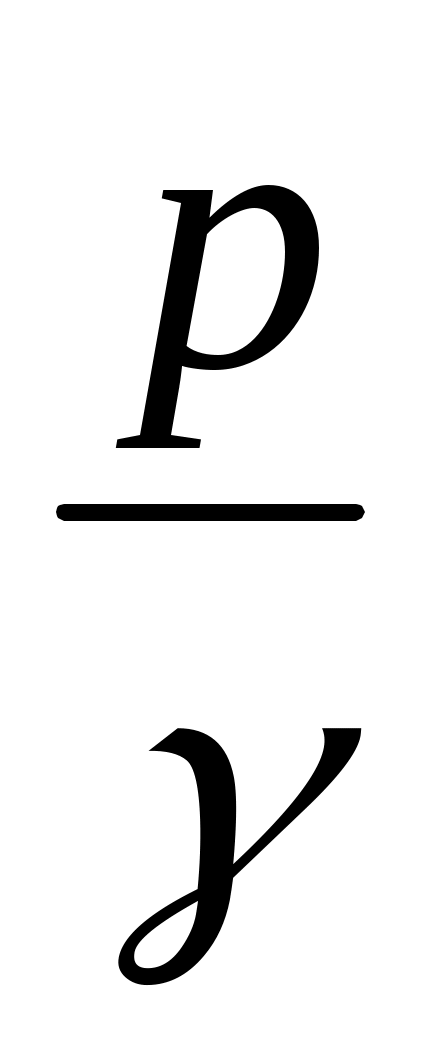 , а затем измерить гидродинамическое давление трубкой Пито, то тогда легко вычислить и величину скорости. Посмотрим, на какой уровень поднимется жидкость в трубке Пито. Составим уравнение Бернули для сечений вдали от трубки Пито и для ее открытого конца (рис. II.08.):
, а затем измерить гидродинамическое давление трубкой Пито, то тогда легко вычислить и величину скорости. Посмотрим, на какой уровень поднимется жидкость в трубке Пито. Составим уравнение Бернули для сечений вдали от трубки Пито и для ее открытого конца (рис. II.08.):
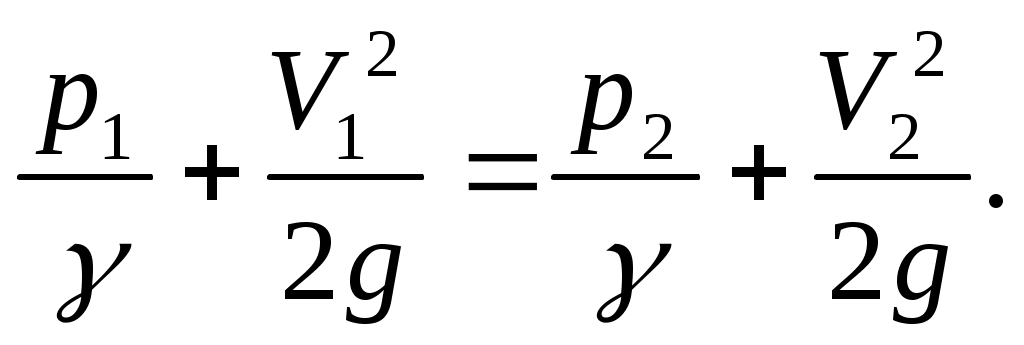
 (II.33)
(II.33)
Но скорость частиц жидкости, набегающих на неподвижную жидкость в конце трубки Пито
, падает до нуля (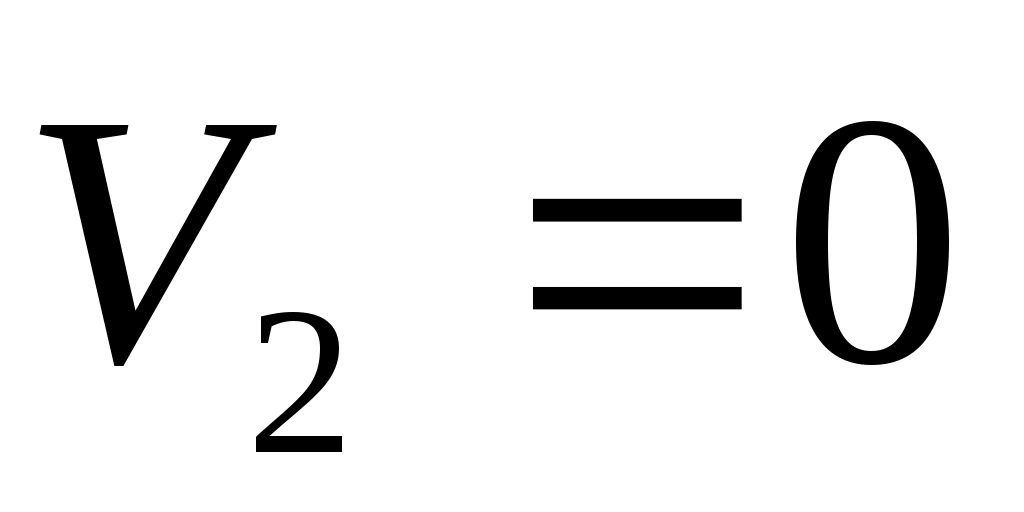 ), и они оказывают на жидкость в трубке Пито дополнительное давление, соответствующее потерянной кинетической энергии
), и они оказывают на жидкость в трубке Пито дополнительное давление, соответствующее потерянной кинетической энергии 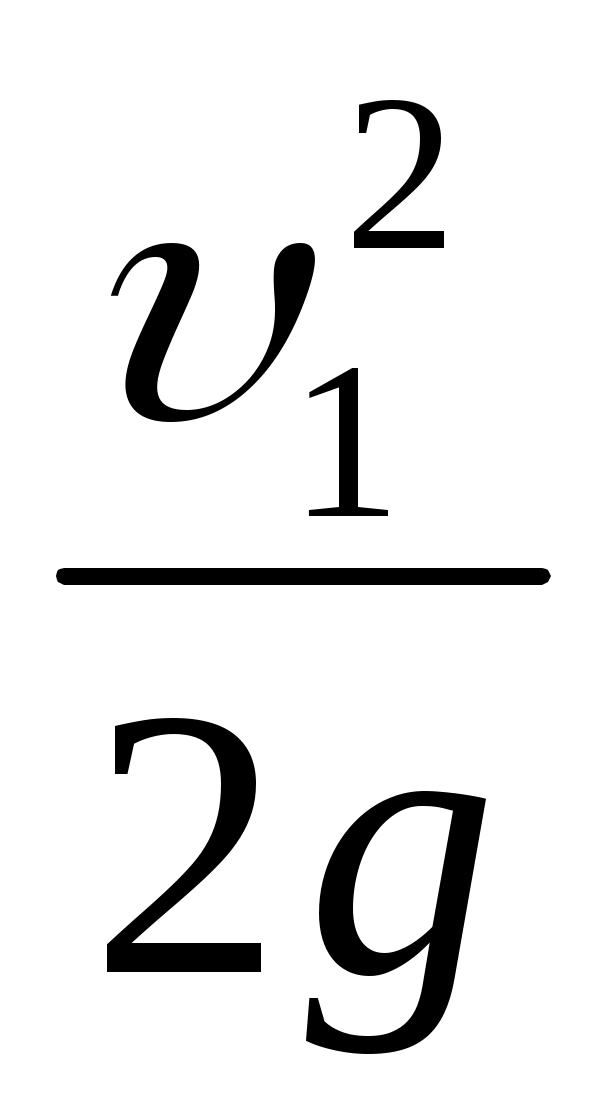 . Действительно, из выражения (II.33) получим:
. Действительно, из выражения (II.33) получим:
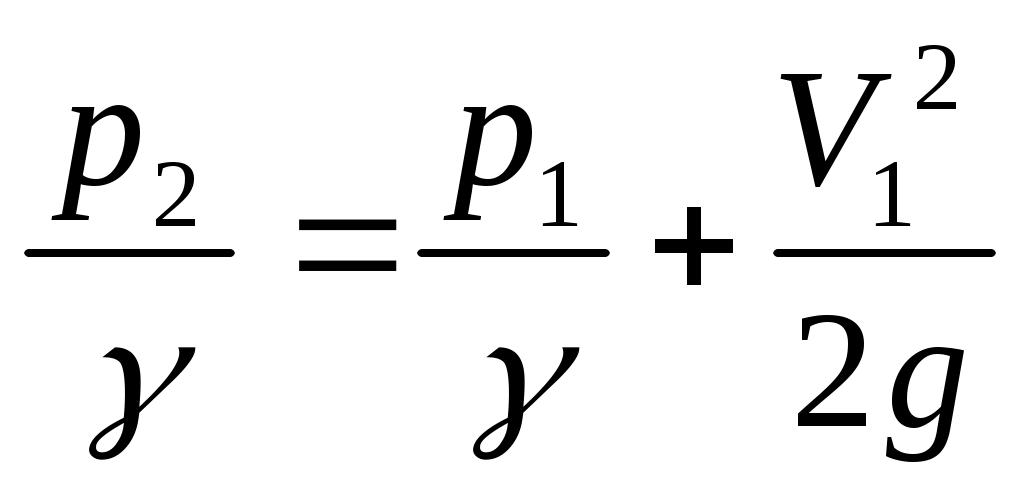 .
.
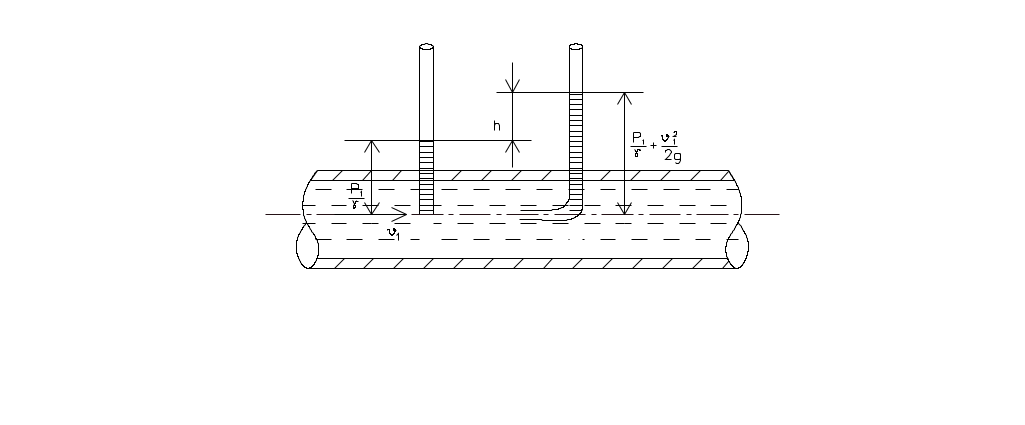
Рис. II.08.
Так как при получении зависимостей (II.31) для водомера Вентури и (II.33) для трубки Пито не учитывались потери напора, то результаты вычислений по этим формулам должны давать несколько завышенные, по сравнению с действительными, значения искомых величин. Поэтому в эти формулы обычно вводятся поправочные коэффициенты, находимые опытным путем.
Из уравнения неразрывности следует, что скорости в сечении 1 и 2 обратно пропорциональны площадям
Представим выражение (11.30) таким образом:
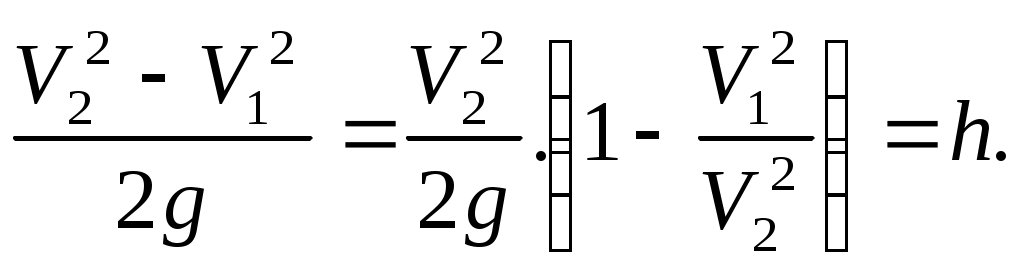 (II.31)
(II.31)Отсюда
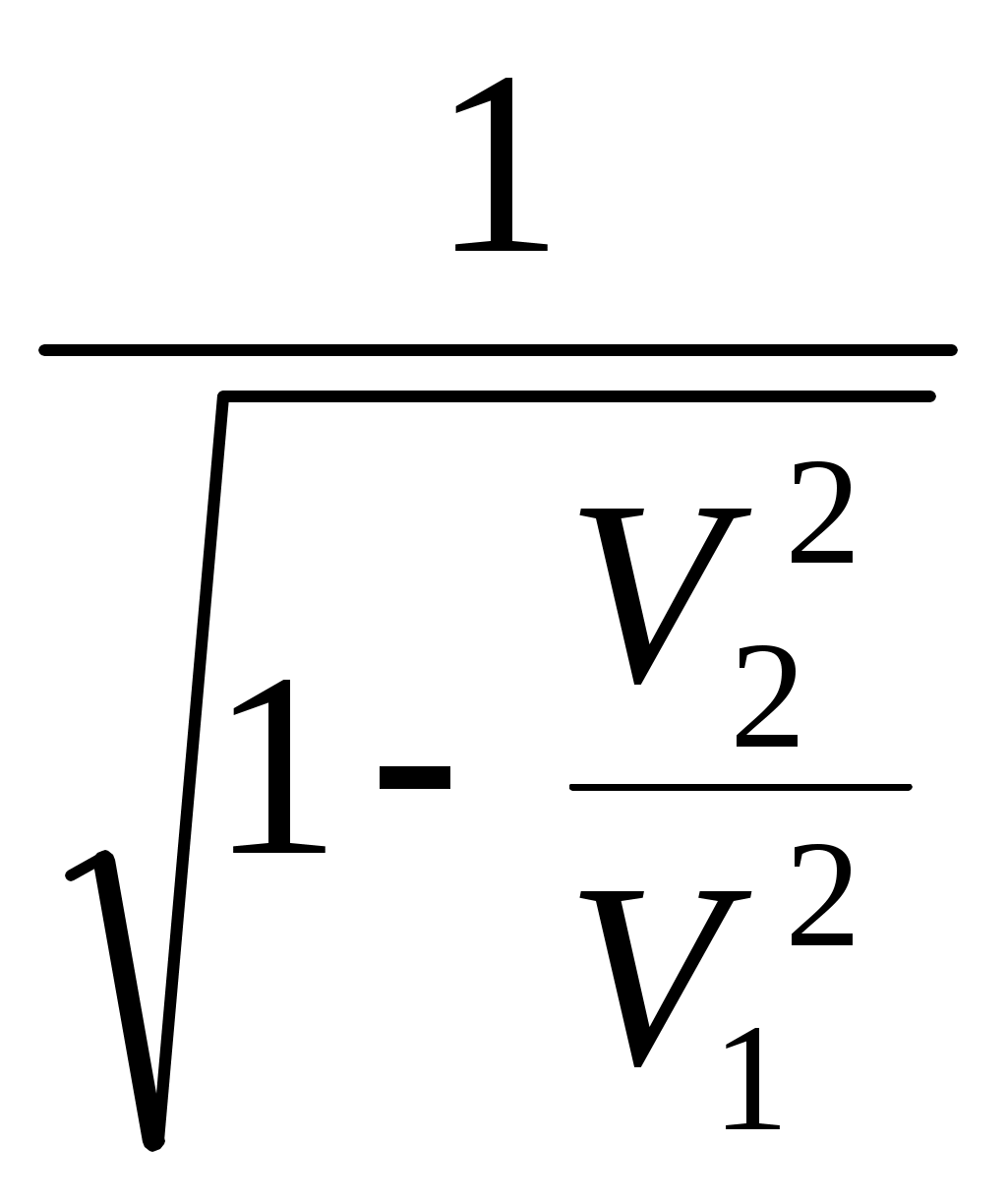
или с учетом (11.31),
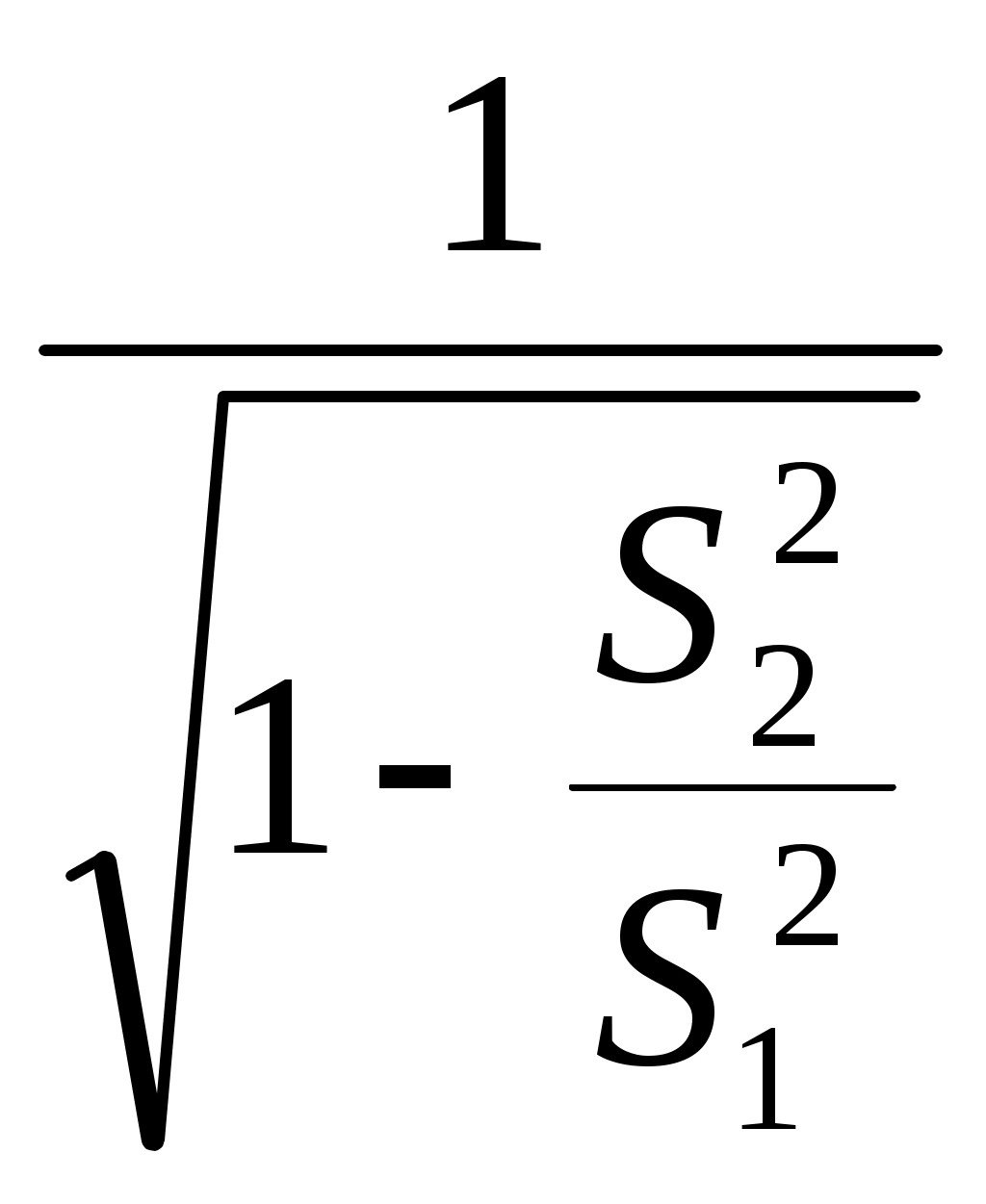

Рис. II.07.
Следовательно,
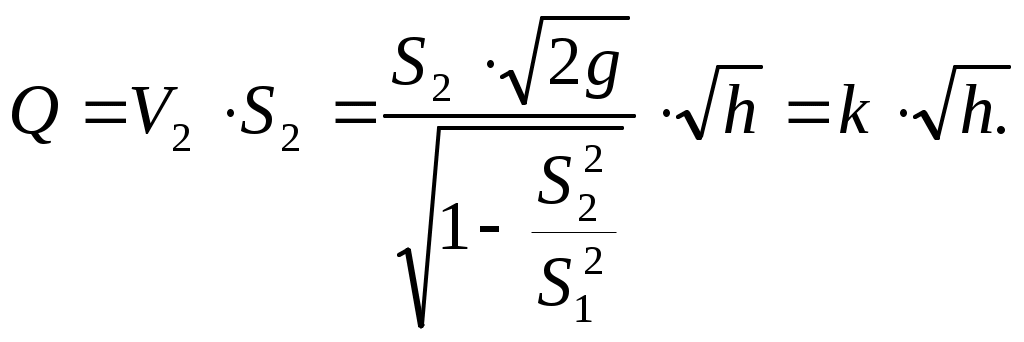 (II.32)
(II.32)Здесь k – константа водомера, постоянная для водомера заданной конструкции и размеров.
Скорость течения жидкости может быть измерена весьма простым прибором, называемым трубкой Пито. Этот прибор представляет собой согнутую под прямым углом трубку, открытый конец которой направляется против течения так, чтобы ее ось совпала с направлением вектора скорости. Если в точке потока, в которой измеряется скорость, предварительно измерить пьезометрический напор
Но скорость частиц жидкости, набегающих на неподвижную жидкость в конце трубки Пито
, падает до нуля (
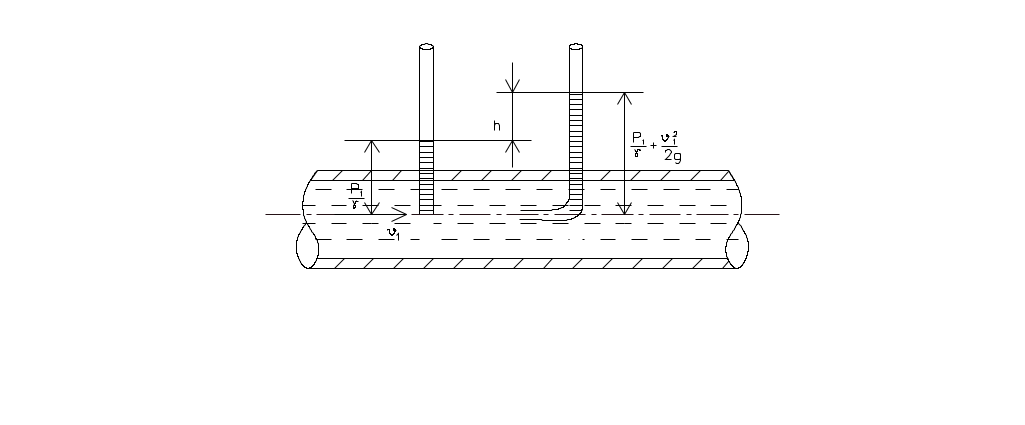
Рис. II.08.
Так как при получении зависимостей (II.31) для водомера Вентури и (II.33) для трубки Пито не учитывались потери напора, то результаты вычислений по этим формулам должны давать несколько завышенные, по сравнению с действительными, значения искомых величин. Поэтому в эти формулы обычно вводятся поправочные коэффициенты, находимые опытным путем.