ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 153
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Очевидно, что для потока в трубе или канале необходимо постоянство расхода, вычисленного по средней скорости wср:
В случае одномерного течения сжимаемой жидкости принцип неразрывности требует постоянства массового расхода, который равен произведению объемного расхода на плотность ρ:
Одномерное течение несжимаемой жидкости является предметом изучения гидравлики. В отличие от нее гидродинамика рассматривает более сложные двухмерные и трехмерные потоки, в которых скорость может изменяться в направлении двух дли трех координатных осей.
Б. Уравнение неразрывности для трехмерного течения несжимаемой жидкости.
Из курса математического анализа известно, что непрерывную функцию, имеющую все непрерывные производные, можно разложить в ряд Тейлора. Поэтому можем для скорости и давления записать следующие разложения
Или, пренебрегая малыми величинами высшего порядка, при стремлении Δl к нулю:
Здесь u и
p и
Эти разложения мы будем пользоваться в дальнейшем при составлении указанных дифференциальных уравнений.
Выберем в потоке фиксированный в пространстве элементарный объем в форме параллелепипеда с ребрами dx, dy, dz (рис. 7). Пусть у левой грани этого объема составляющая скорости в направлении оси x равна ux. По достижении правой грани эта составляющая может измениться и стать равной
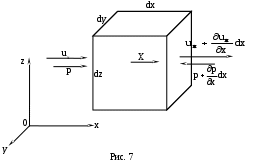
Через левую грань за единицу времени втекает внутрь параллелепипеда объем жидкости, равный произведению нормальной составляющей скорости на площадь грани: wxdydz.
Через правую грань вытекает объем
Суммарное поступление жидкости через левую и правую грани равно разности:
Аналогично получим, что через грани, перпендикулярные оси у (задняя и передняя грани на рис. 7), Суммарное поступление жидкости внутрь параллелепипеда равно
Разделив последнее равенство на объем параллелепипеда dxdydz, получим уравнение неразрывности в дифференциальной форме
При выводе уравнения неразрывности мы не учитывали сжимаемости жидкости. В наиболее общем случае неустановившегося движения сжимаемой жидкости уравнение неразрывности имеет вид (приводится без вывода):
2.2. Уравнения движения идеальной жидкости Эйлера
Идеальной жидкости, лишенной свойства вязкости, в природе не существует. Опыт показывает, однако, что при обтекании некоторых тел маловязкой жидкостью (такой, как вода, воздух) торможение из-за вязкого трения охватывает лишь тонкий пристенный слой. За пределами этого слоя вязкость оказывает пренебрежимо малое влияние на распределение скоростей и давлений. Поэтому для изучения внешнего потока возможно использовать методы динамики идеальной жидкости, что существенно упрощает задачу по сравнению с динамикой вязкой жидкости. Пренебрежение вязкостью помогает также решать в первом приближении задачи одномерного течения.
А. Вывод уравнений. Уравнения гидродинамики Эйлера выражают в применении к жидкой частице второй закон Ньютона: «Произведение массы частицы на ускорение равно действующей силе», т.е.
Здесь
Применим второй закон Ньютона к частице жидкости в форме параллелепипеда с малыми ребрами dx, dy, dz (см. рис. 7). Рассмотрим проекции записанного выше векторного равенства на координатные оси, причем начнем с проекции на ось x:
Здесь ux и fx – составляющие скорости и силы по оси x. Масса m равна произведению плотности ρ на объем частицы, или ρdxdydz.
К силам, действующим на частицу, относится разность давлений на грани, перпендикулярные оси x. Если давление у левой грани (см. рис. 7) равно p, то у правой грани
Кроме силы давления частица может испытывать действие в направлении оси x внешних объемных сил (например, силы тяжести или инерции). Если проекцию ускорения, создаваемого внешними силами в направлении оси х, обозначить через X, м/сек
2 (см. п.2.1), то сама сила окажется равна произведению ускорения на массу частицы, т.е. Хρdxdydz, н (или кгс). Подставляя полученные величины в уравнение (II.8) и пользуясь аналогичными рассуждениями для проекций ускорений и сил на координатные оси y и z, получим систему дифференциальных уравнений гидродинамики Эйлера:
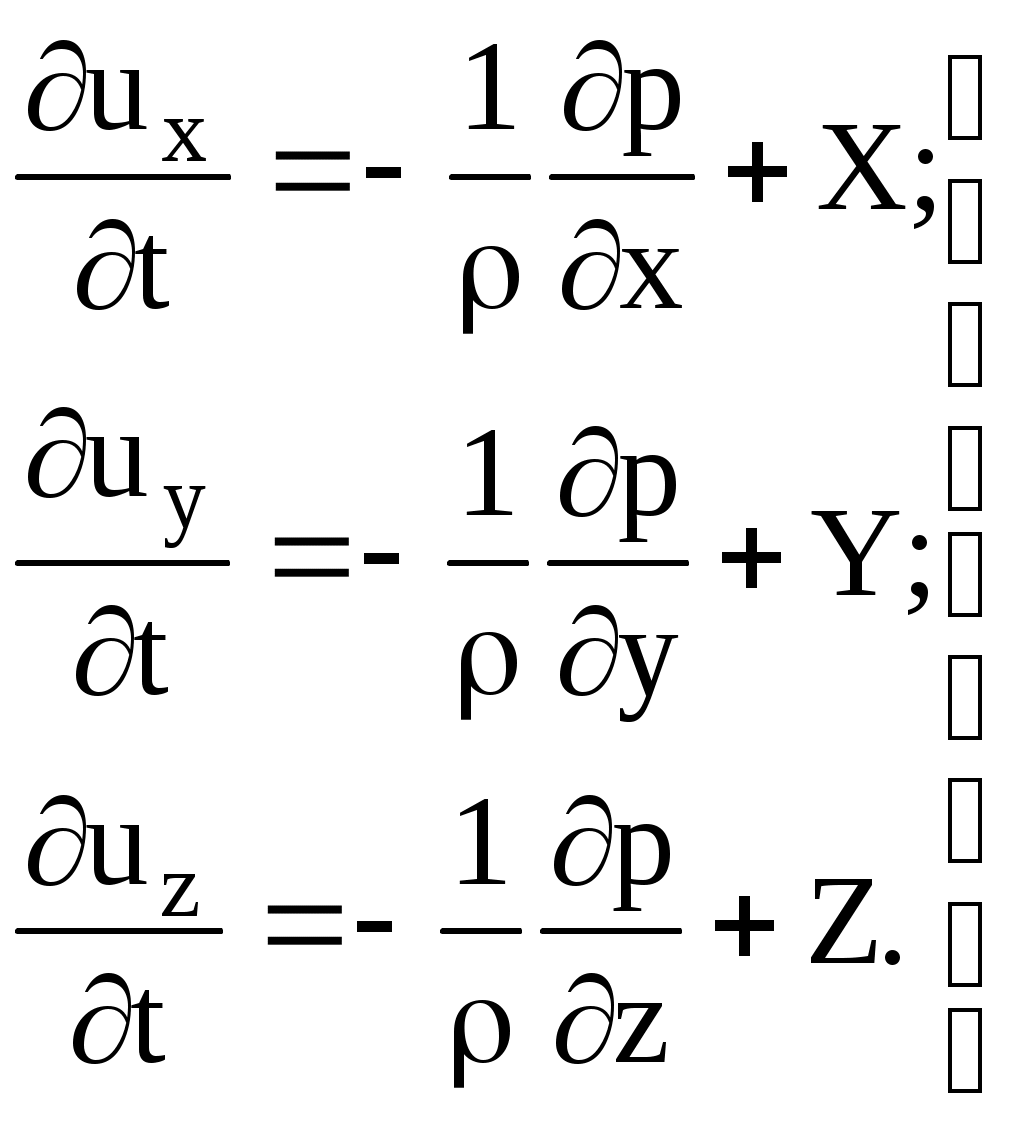 (II.9)
(II.9)Здесь Y, Z – проекции ускорений объемных сил на оси y, z.
Дифференциальные уравнения Эйлера показывают, что ускорение частиц (левые части записанных уравнений) обусловлено перепадом давления (первые члены правых частей) и действием внешних объемных сил. В реальной жидкости, если скорости распределены неравномерно, возникают еще касательные напряжения вследствие вязкости, которые мы не учитывали при выводе уравнений движения идеальной жидкости.
Если из внешних сил на движущуюся жидкость действует только сила тяжести с ускорением g, представляется целесообразным выбрать систему координат так: плоскость ху расположить горизонтально, а ось z направить вертикально вверх. Тогда уравнения Эйлера примут вид:
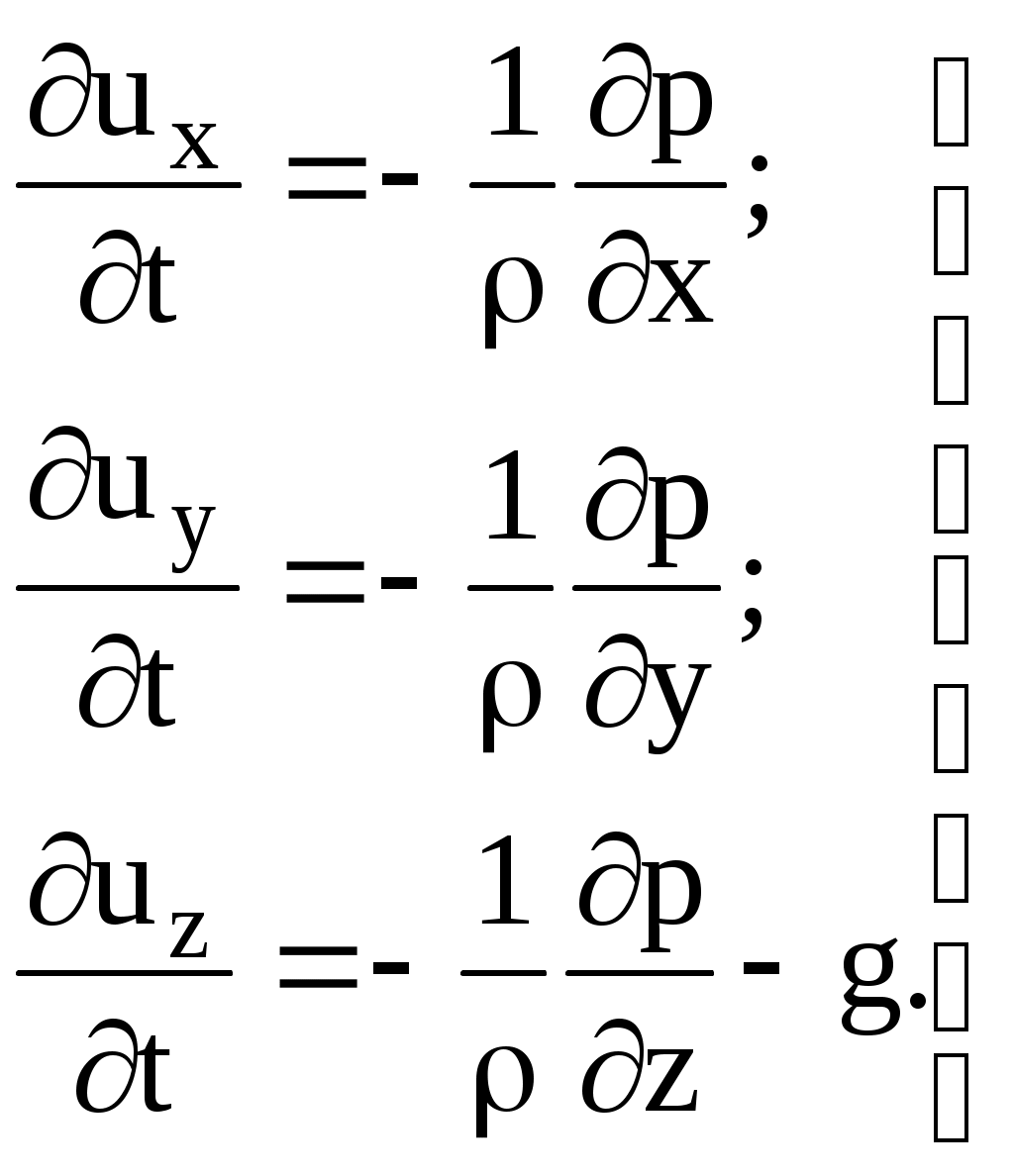 (II.9а)
(II.9а)Уравнения Эйлера (II.9) совместно с уравнением неразрывности для несжимаемой жидкости (II.7) образуют систему четырех уравнений, содержащую четыре неизвестных: wx, wy, wz, p. В случае сжимаемой жидкости (газа) к уравнениям Эйлера и неразрывности необходимо добавить еще уравнение, дающее связь между давлением и плотностью жидкости:
Интегрируя полученную замкнутую систему уравнений при за/-данных граничных и начальных условиях, можно в принципе определить вектор скорости и давление в любой точке потока и в любой момент времени.
Б. Граничные и начальные условия. Граничные условия при обтекании тела задают распределение скоростей вдали от тела, где не сказывается его искажающее влияние на поток, и на поверхности тела. Согласно принципу относительности движения, известному из механики, задача о движении тела в неподвижной жидкости (например, самолета, корабля) в динамическом отношении тождественна задаче об обтекании неподвижного тела равномерным потоком. Поэтому гидромеханика широко использует принцип «обращения движения». Граничные условия для обращенной задачи о движении тела в неподвижной жидкости обычно задаются следующим образом:
1. Условия «на бесконечности». В удалении от_обтекаемого тела задаются давление
2. Условие «непроницаемости». Пусть n – нормаль к поверхности обтекаемого тела. Если жидкость через поверхность не протекает, то нормальная составляющая скорости равна нулю: wn = 0, и скорость течения на поверхности тела может быть только касательной к ней.
Начальные условия характеризуют состояние потока в некоторый конкретный момент. При установившемся движении скорость и давление в данной тючке не меняются во времени и начальные условия не задаются.
В общем случае пространственного (трехмерного) потока, когда скорость изменяется в направлении всех трех координатных осей, интегрирование системы уравнений движения и неразрывности встречает чрезвычайные математические трудности. Поэтому задача решается при внесении различных упрощающих предположений. Наиболее полно разработана теория одномерного движения. Для несжимаемой жидкости эта теория составляет основу гидравлики.
При одномерном течении граничные условия задают величины скорости и давления на сечениях, ограничивающих заданный участок струйки (потока).
2.3. Уравнение Д. Бернулли для элементарной струйки идеальной жидкости
Выше были получены дифференциальные уравнения движения идеальной жидкости и уравнение неразрывности движения, образующие замкнутую систему уравнений. Для решения конкретных инженерных задач необходимо уметь находить интегралы этих уравнений. Методы решения дифференциальных уравнений в частных производных (так называемые уравнения математической физики) приводятся в соответствующих разделах высшей математики. Сразу же оговоримся, что рассматриваемая система уравнений настолько сложа, что до настоящего времени еще не получено ее решение в общем виде. Однако для некоторых частных случаев движения жидкости решение этих уравнений может быть получено. В частности, эта система сможет быть проинтегрирована, если рассматривать установившиеся движение идеальной жидкости вдоль линии тока (или в элементарной струйке).