ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 149
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и  (постоянные величины).
(постоянные величины).
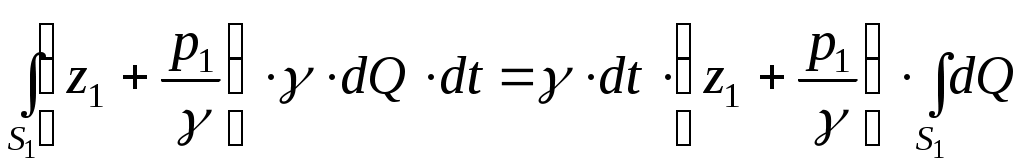 .
.
Но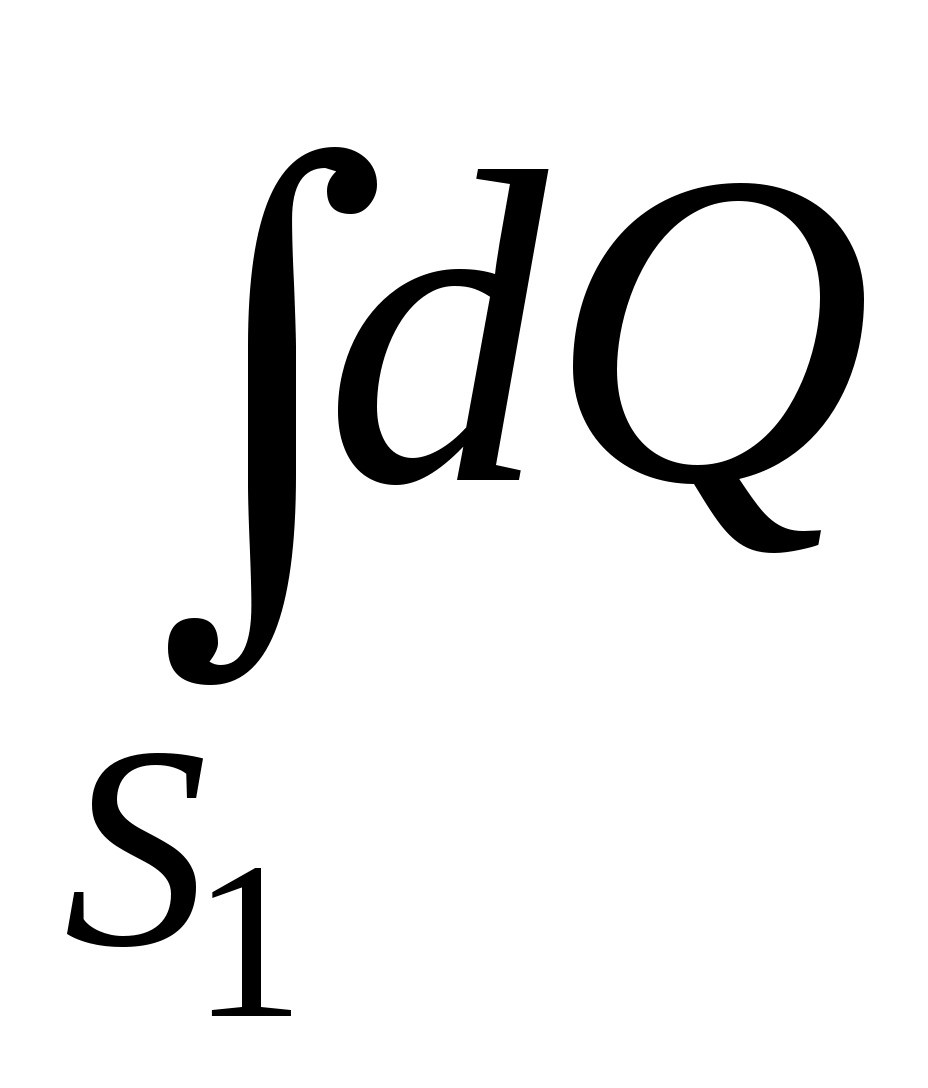 представляет собой расход потока Q. Поэтому:
представляет собой расход потока Q. Поэтому:
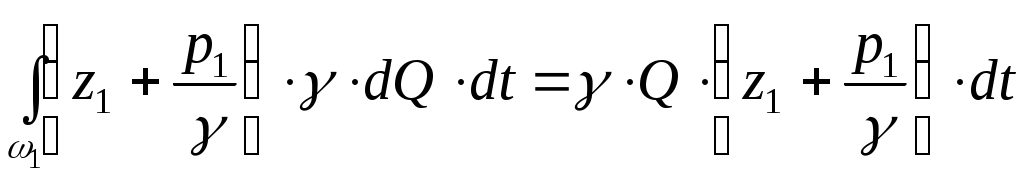 . (II.21)
. (II.21)
Запишем второй интеграл в следующем виде:
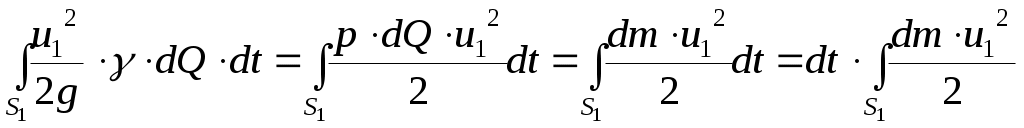
Этот интеграл представляет собой, как уже указывалось, кинетическую энергию, проносимую потоком через сечение 1-1 за время . Для его вычисления необходимо знать, каким образом распределяются скорости движения частиц жидкости по живому сечению. Если вычислить кинетическую энергию потока в предположении и постоянстве этих скоростей (другими словами, по средней скорости потока в данном живом сечении
. Для его вычисления необходимо знать, каким образом распределяются скорости движения частиц жидкости по живому сечению. Если вычислить кинетическую энергию потока в предположении и постоянстве этих скоростей (другими словами, по средней скорости потока в данном живом сечении 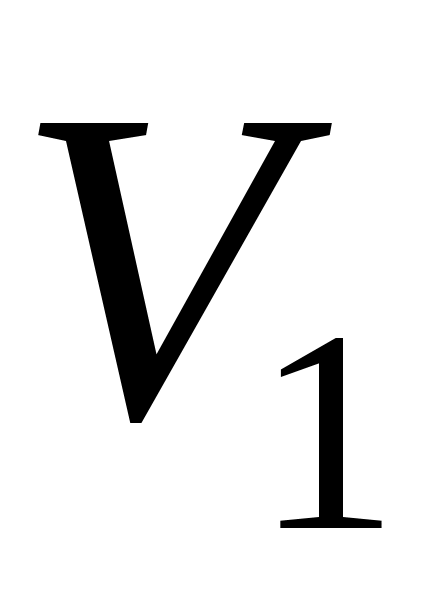 , то получим:
, то получим:
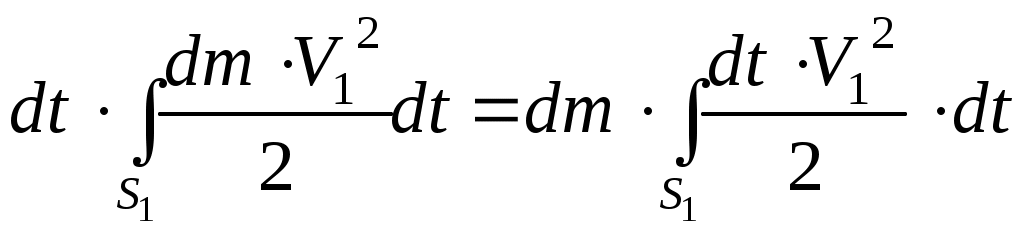 .
.
Это выражение по величине всегда меньше, чем действительная кинетическая энергия, вычисленная по действительным скоростям. обозначим отношение этих двух величин :
:
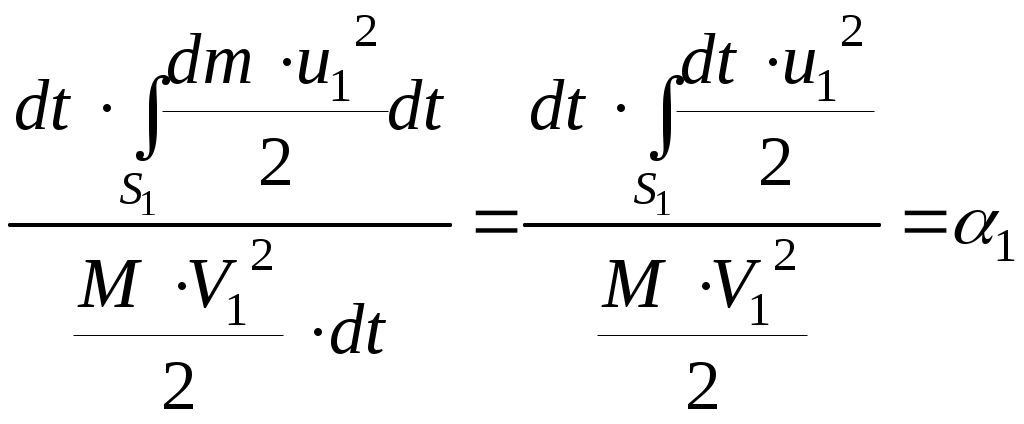 . (II.02)
. (II.02)
Коэффициент называется коэффициентом кинетической энергии потока и представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости потока. Очевидно, что этот коэффициент всегда больше единицы.
называется коэффициентом кинетической энергии потока и представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости потока. Очевидно, что этот коэффициент всегда больше единицы.
Возвращаясь к поставленной задаче о вычислении второго интеграла в выражении (11.20), констатируем, что его значение можно выразить через среднюю скорость посредством введения коэффициента кинетической энергии :
:
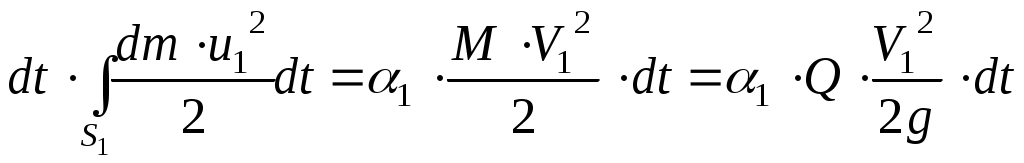
(II.23)
Подставив значения интегралов (11.21) и (11.23) в зависимость (11.20), получим:
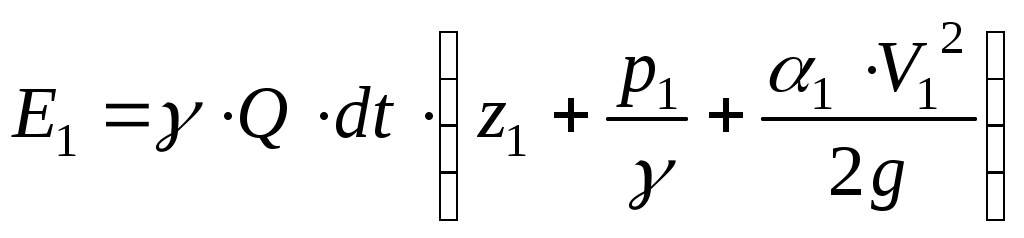 (II.24)
(II.24)
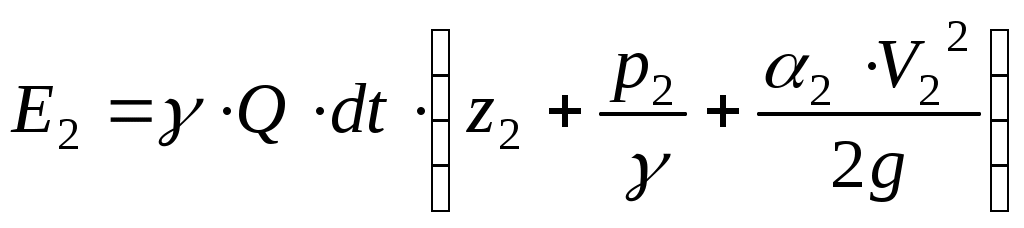 (II.25)
(II.25)
Поделив выражения (11.24) и (11.25) на вес жидкости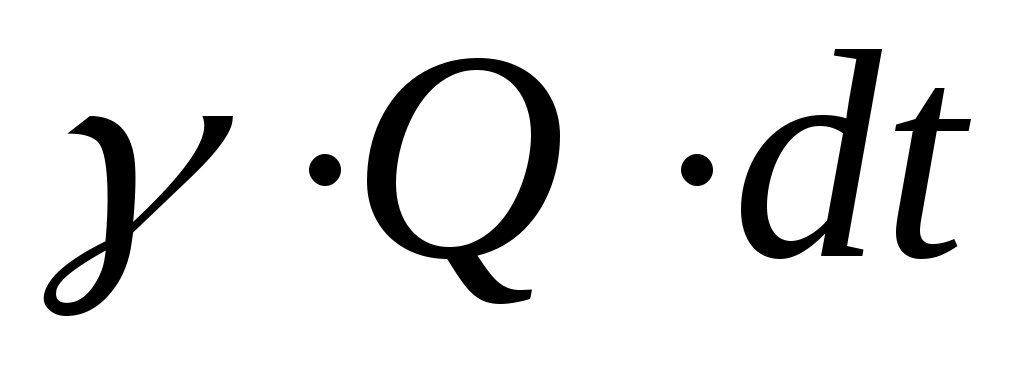 , получим значения полных удельных энергий потока в этих сечениях:
, получим значения полных удельных энергий потока в этих сечениях:
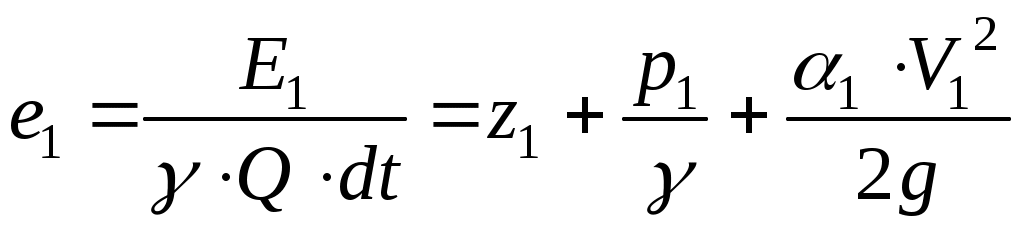 ;
;
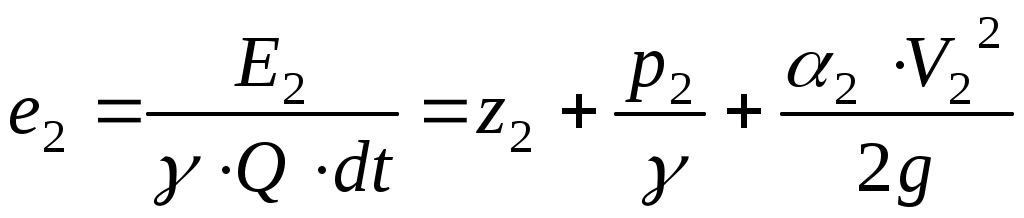 .
.
Так как на участке потока между сечениями 1-1 и 2-2 часть энергии потока затрачивается на преодоление гидравлических сопротивлений и необратимо превращается в тепловую энергию,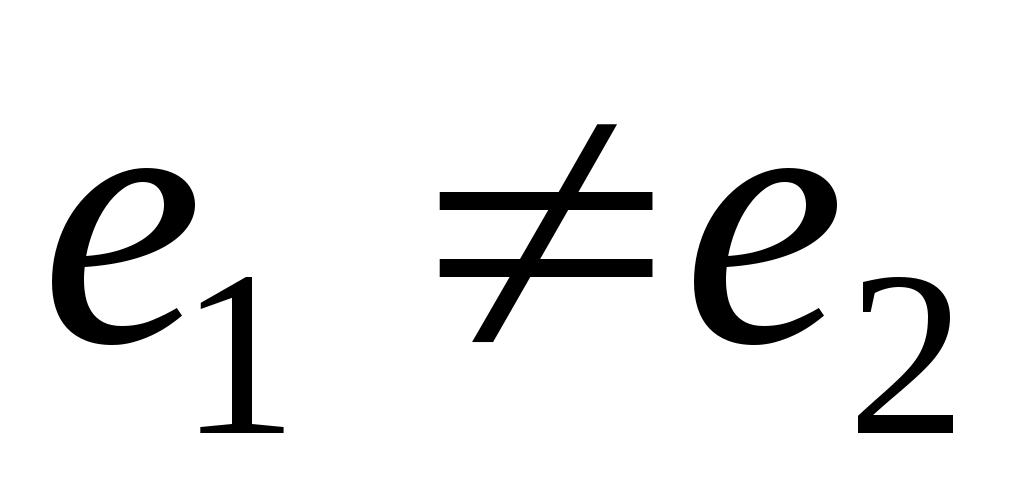 . Очевидно также, что
. Очевидно также, что 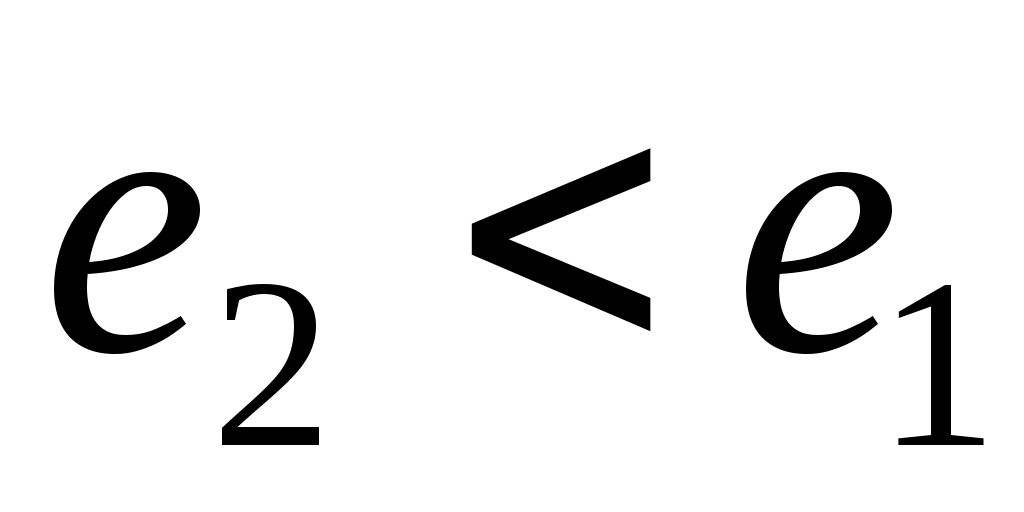 . Разница между этими удельными энергиями выразит потери удельной энергии потока на рассматриваемом участке движения:
. Разница между этими удельными энергиями выразит потери удельной энергии потока на рассматриваемом участке движения:
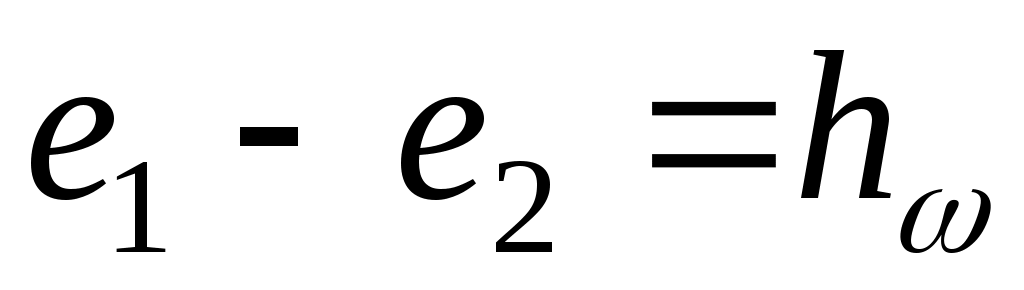 .
.
Тогда:
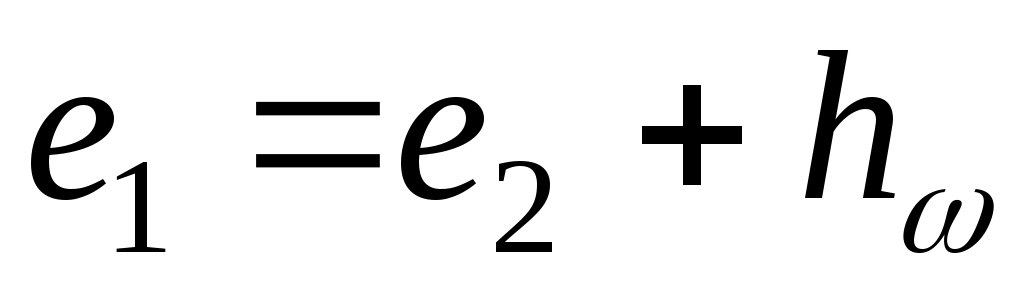 ,
,
или
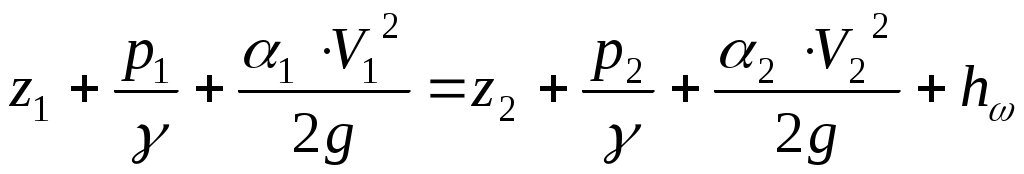 (II.26)
(II.26)
Полученное уравнение и есть уравнение Д.Бернулли для установившегося потока реальной жидкости. По внешнему виду оно почти не отличается от полученного ранее уравнения Бернулли для элементарной струйки реальной жидкости. Тем не менее это уравнение обладает рядом отличительных особенностей, которые необходимо всегда помнить для правильного его использования.
Во-первых, это уравнение записывается не для отдельных частиц жидкости, находящихся на одной и той же линии тока, а для различных сечений потока, при этом совершенно различно, какую частицу жидкости в сечении мы выбираем для определения величин и
и  , так как при плавно изменяющемся движении
, так как при плавно изменяющемся движении 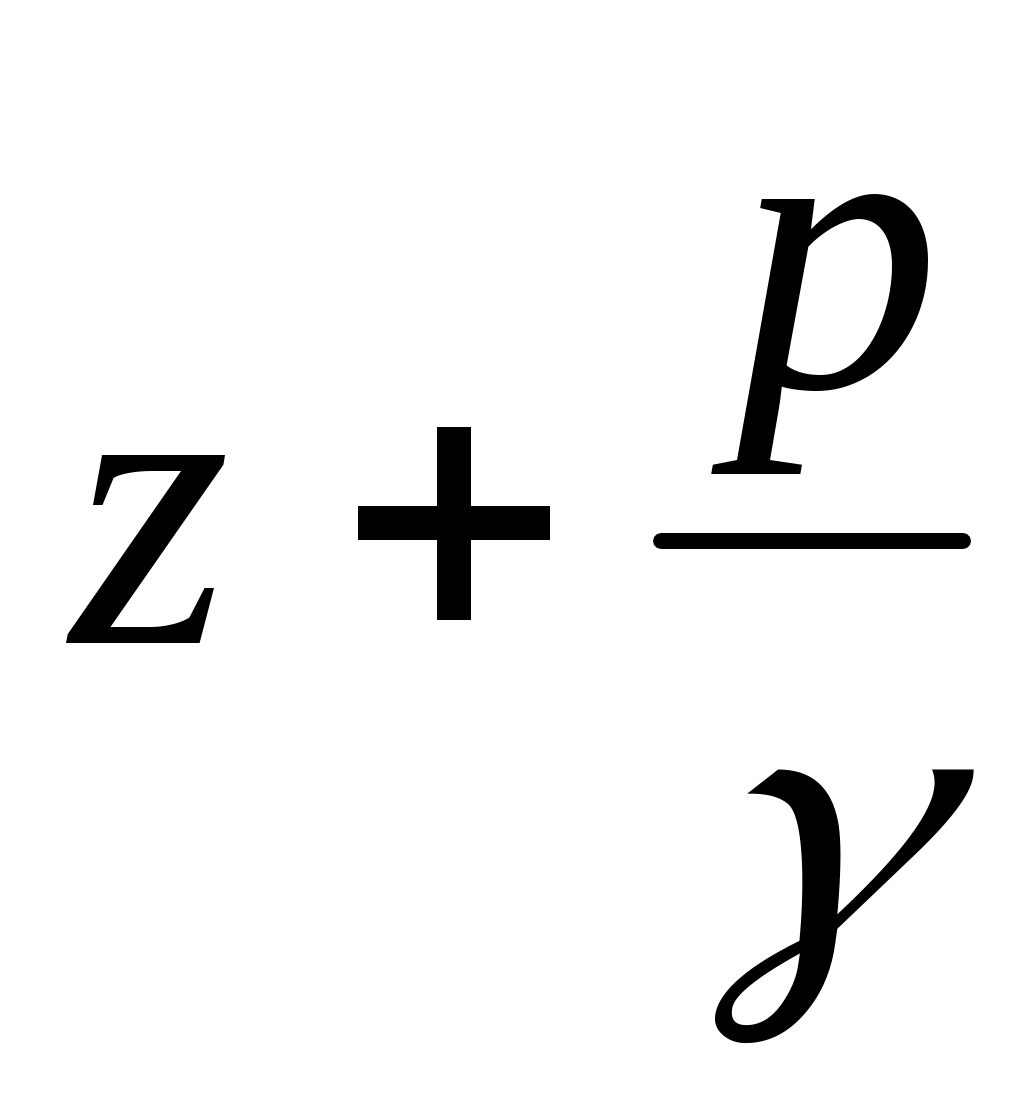 сохраняет постоянное значение для всех частиц жидкости в данном живом сечении. Необходимо лишь, чтобы значения
сохраняет постоянное значение для всех частиц жидкости в данном живом сечении. Необходимо лишь, чтобы значения
 и
и  соответствовали, хотя и произвольной, но обязательно одной и той же частице.
соответствовали, хотя и произвольной, но обязательно одной и той же частице.
Во-вторых, не обязательно, чтобы поток на всем протяжении между рассматриваемыми сечениями, для которых составляется уравнение Д.Бернулли, был близким к параллельноструйчатому. На этом участке он может претерпевать весьма резкие изменения своей формы. Совершенно необходимо лишь, чтобы в сечениях, для которых записывается уравнение Д.Бернулли, движение было плавно изменяющимся.
Изменение формы (деформация) потока сопровождается затратами удельной его энергии и учитывается членом .
.
По аналогии с предыдущим будем называть величину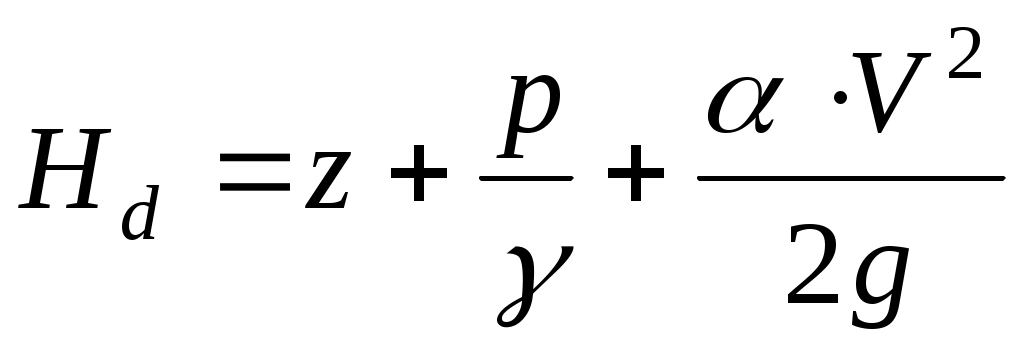 - гидродинамическим напором потока, величину
- гидродинамическим напором потока, величину 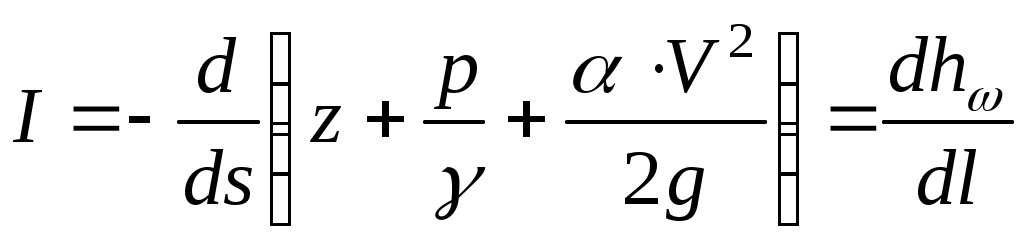 - гидравлическим уклоном потока, а величину
- гидравлическим уклоном потока, а величину 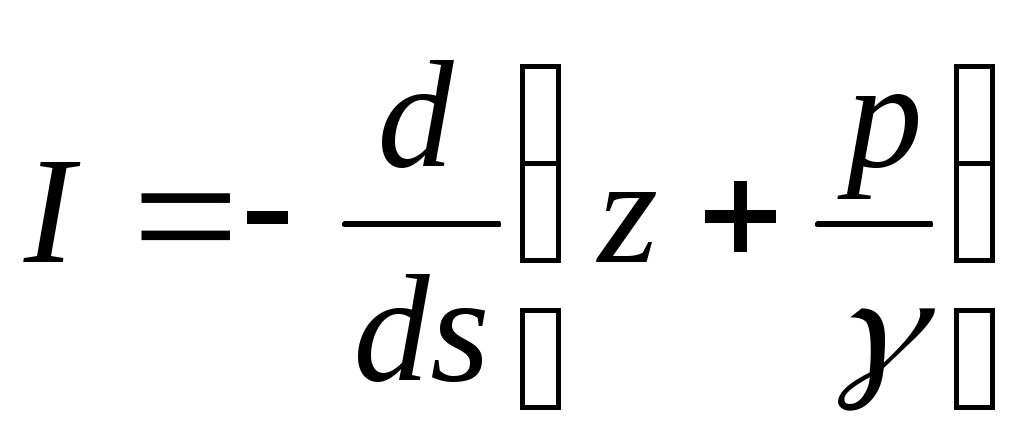 - пьезометрическим уклоном потока.
- пьезометрическим уклоном потока.
Отметим, что при равномерном движении, когда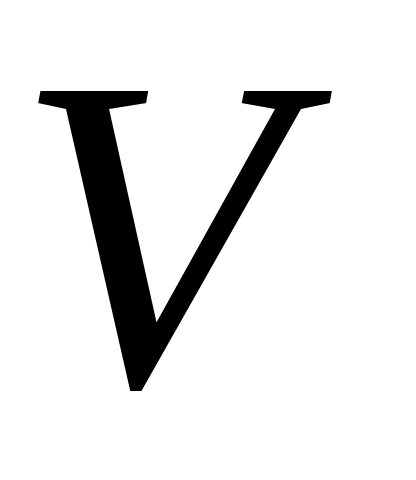 не изменяется по длине потока, то есть
не изменяется по длине потока, то есть 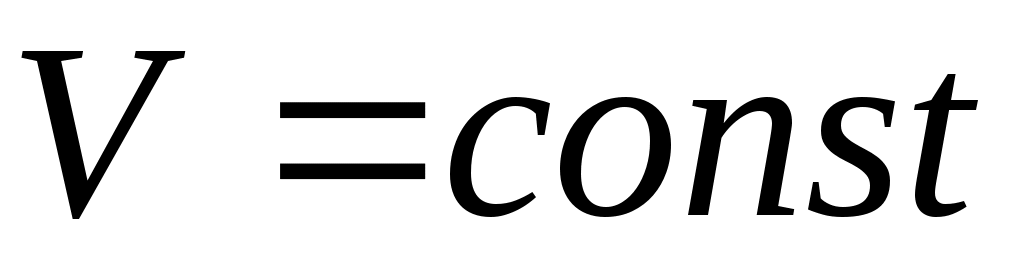 , гидравлический и пьезометрический уклоны совпадают:
, гидравлический и пьезометрический уклоны совпадают:

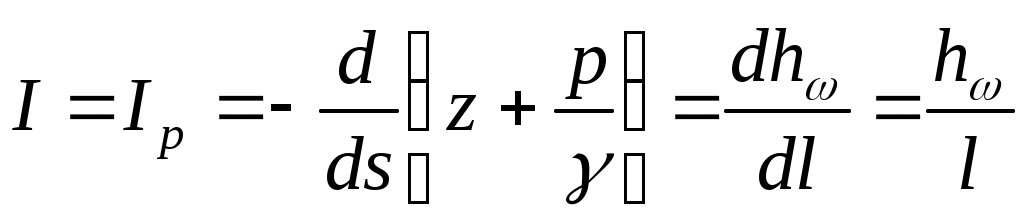 . (II.27)
. (II.27)
Практическое использование уравнения Д.Бернулли
«Уравнение Бернулли имеет чрезвычайно важное значение в гидравлике, позволяя по двум известным элементам их трех (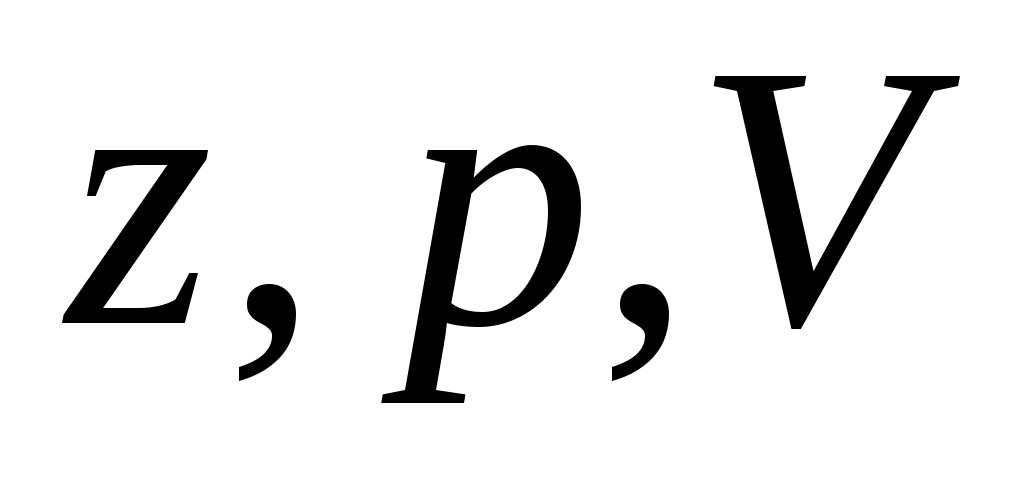 ) определить третий. Нередко это уравнение является наиболее действительным средством как для исследования различных теоретических вопросов гидравлики, так и для решения многих практических задач, выдвигаемых инженерной практикой, а поэтому его можно считать фундаментальным для гидравлики уравнением движения», - так определил значение уравнения Бернулли академик Н.Н.Павловский.
) определить третий. Нередко это уравнение является наиболее действительным средством как для исследования различных теоретических вопросов гидравлики, так и для решения многих практических задач, выдвигаемых инженерной практикой, а поэтому его можно считать фундаментальным для гидравлики уравнением движения», - так определил значение уравнения Бернулли академик Н.Н.Павловский.
С помощью уравнения Бернулли легко объяснить ряд явлений, наблюдаемых в технике и повседневной жизни. Так, например, очень легко установить характер распределения давлений в горизонтальной трубе переменного сечения (рис. II.06). Действительно, применяя уравнение неразрывности к двум сечениям, показанным на рисунке, устанавливаем, что в узкой части поток обладает большими средними скоростями, чем в широкой части: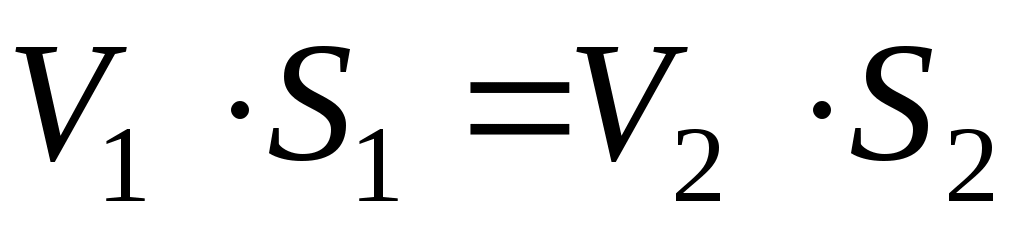 и
и 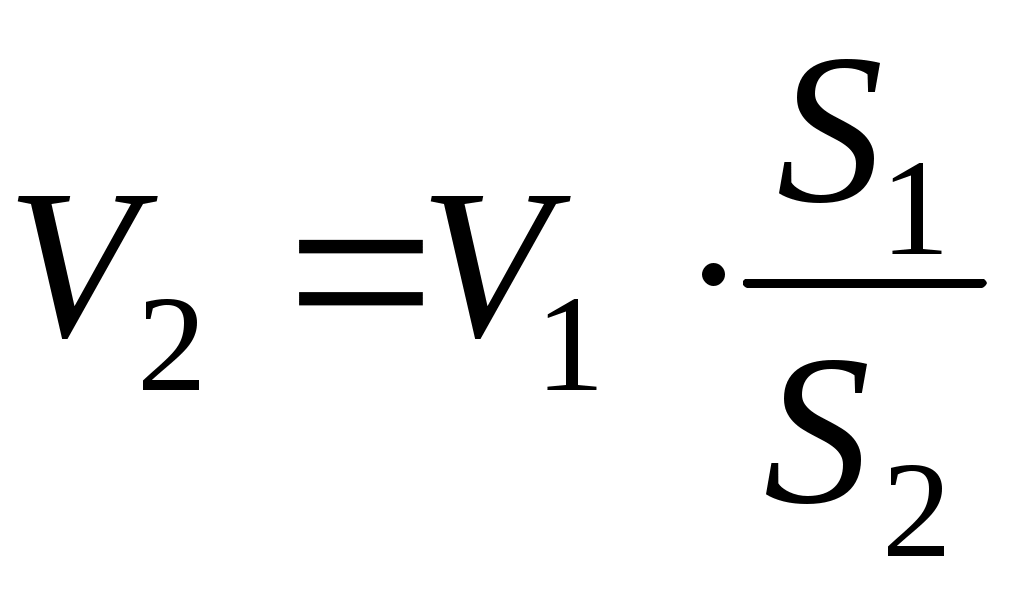 , поэтому
, поэтому 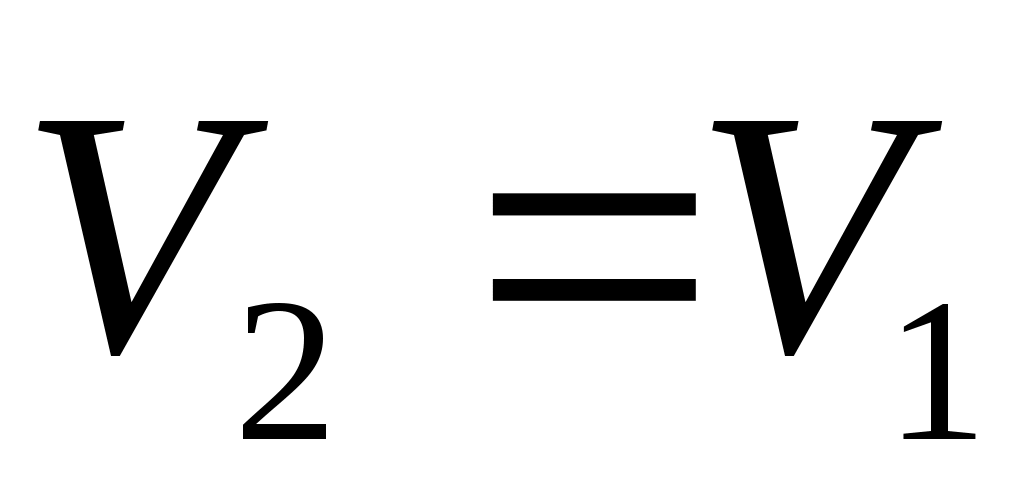 .
.
Запишем уравнение Бернулли для этих же сечений потока. Это воз можно сделать, так как движение вблизи выбранных сечений удовлетворяет условиям плавно изменяющегося движения. Труба расположена горизонтально, и если выбрать для определения величин
можно сделать, так как движение вблизи выбранных сечений удовлетворяет условиям плавно изменяющегося движения. Труба расположена горизонтально, и если выбрать для определения величин  и
и  в сечениях 1-1 и 2-2 частицы жидкости, расположенные на ее оси. То для этих частиц значения
в сечениях 1-1 и 2-2 частицы жидкости, расположенные на ее оси. То для этих частиц значения  и
и  будут одинаковыми
будут одинаковыми 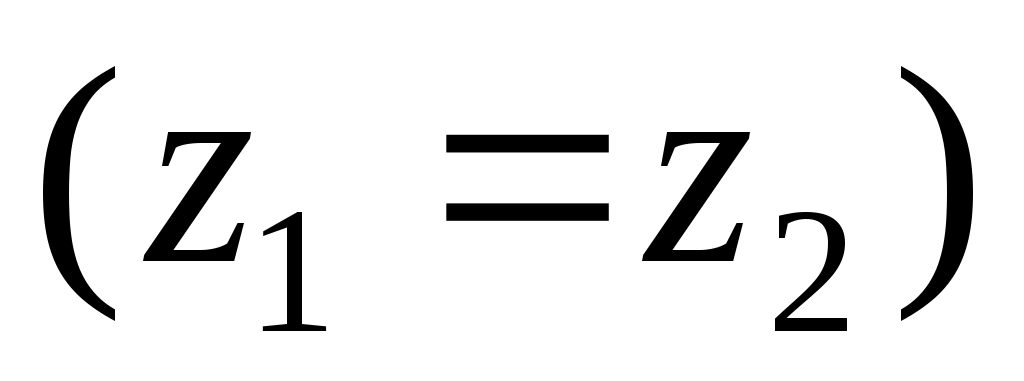 . пренебрегая величиной потерь на участке потока 1-2 (
. пренебрегая величиной потерь на участке потока 1-2 (
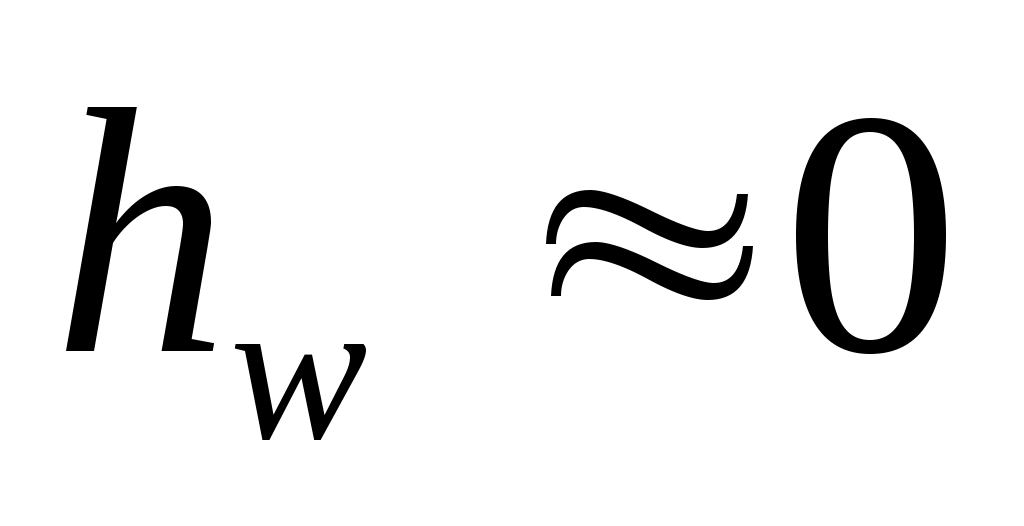 ) и неравномерностью распределения скоростей в сечениях (
) и неравномерностью распределения скоростей в сечениях (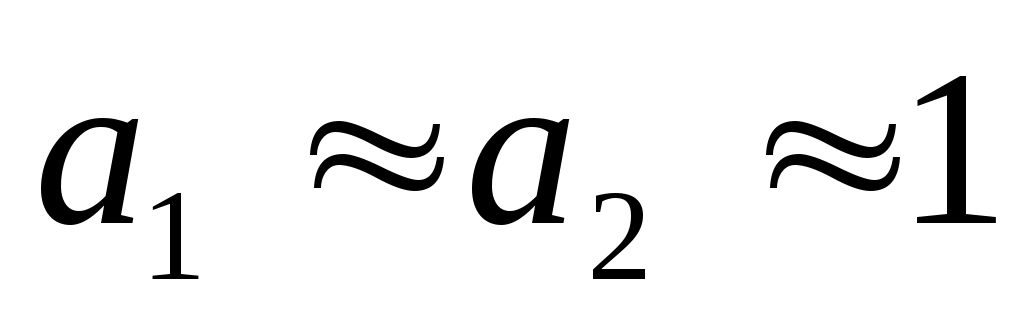 ), запишем уравнение Бернулли в следующем виде:
), запишем уравнение Бернулли в следующем виде:
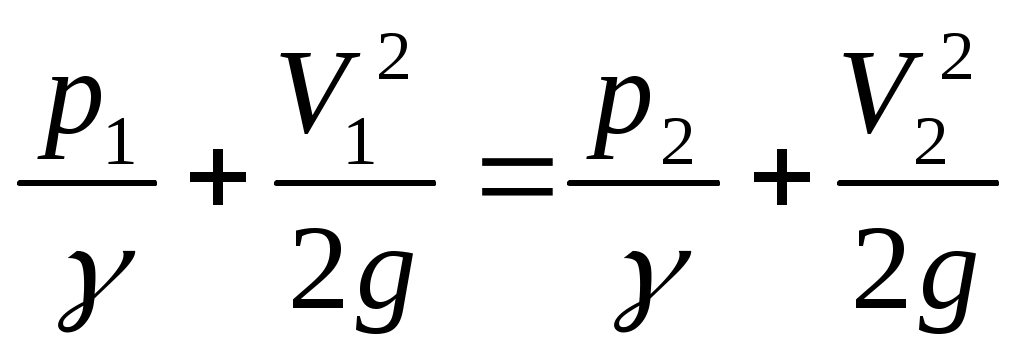 .
.
Отсюда найдем:
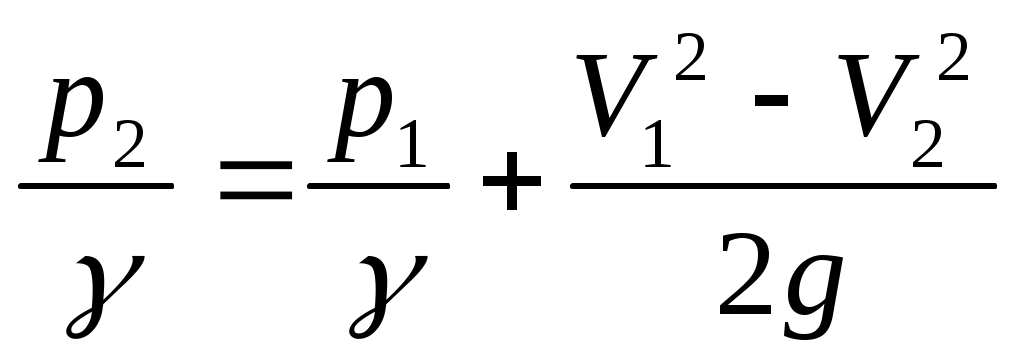 . (II.28)
. (II.28)
Но ранее было установлено, что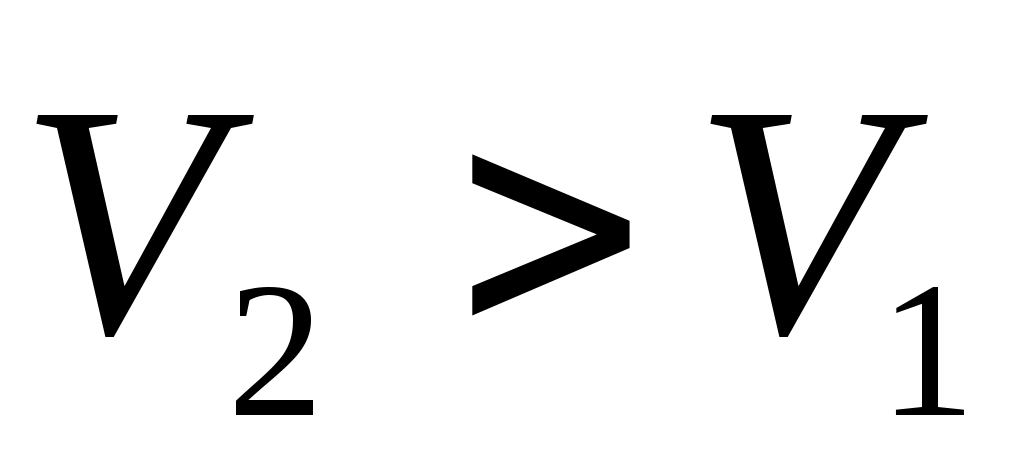 , поэтому разность
, поэтому разность 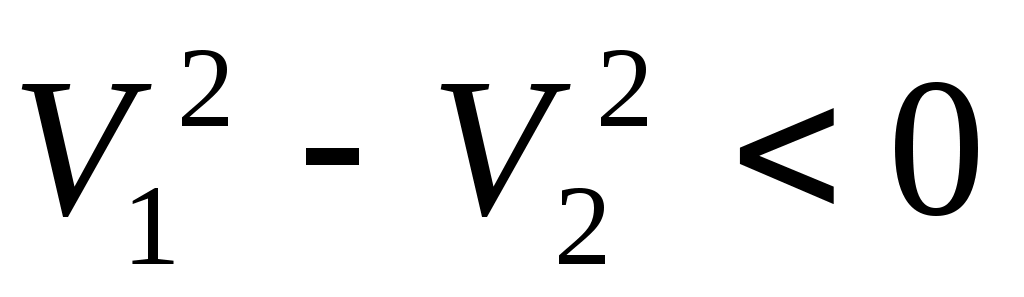 , и, следовательно, давление
, и, следовательно, давление 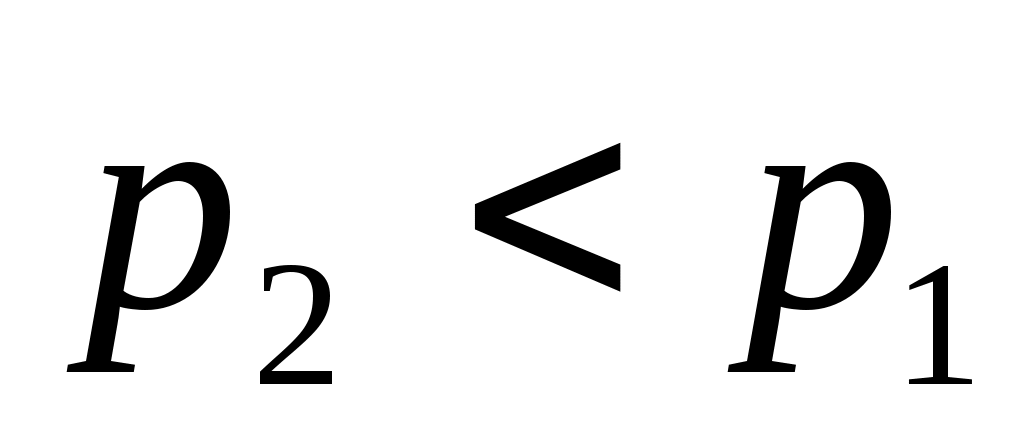 .
.
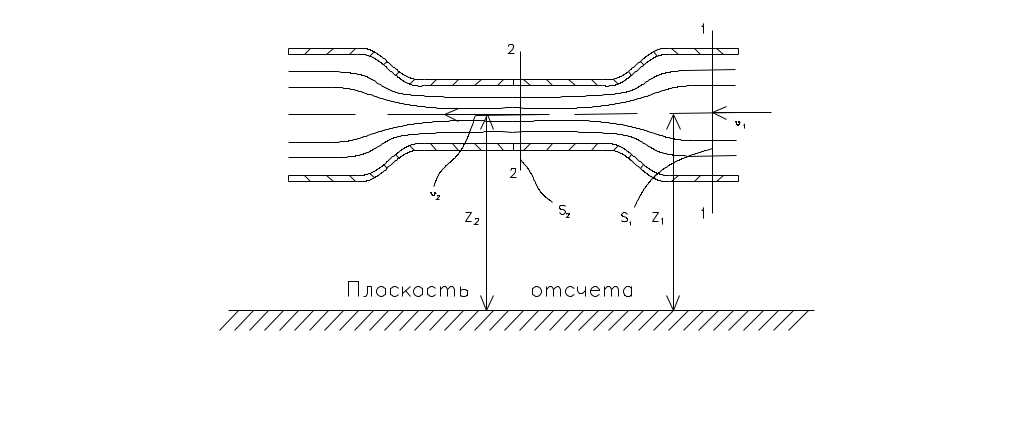
Рис. II.06.
Полученный результат подчеркивает специфическую особенность жидкостей преобразовывать кинетическую энергию давления (и наоборот), что очень хорошо используется в технике и находит самые разнообразные применения. Так, например, пропуская жидкость с большими скоростями через суженные сечения, можно значительно понизить в этом сечении давление и создать благоприятные условия для всасывания жидкости. Этот принцип используется для создания различных струйных аппаратов (водоструйных и пароструйных насосов и т.п.). Очень широко используется тот же принцип в измерительной технике для определения установившихся расходов жидкости и скоростей ее движения.
Рассмотрим так называемый водомер Вентури, который служит для измерения расхода жидкости и представляет собой короткий двухконусный патрубок, сначала суживающийся, а затем расширяющийся (рис. II.06.), вмонтированный в короткий трубопровод.
Записывая уравнение Бернули для сечений 1 и 2, получим при тех же предположениях, что и выше, зависимость (11.29), которую перепишем в виде:
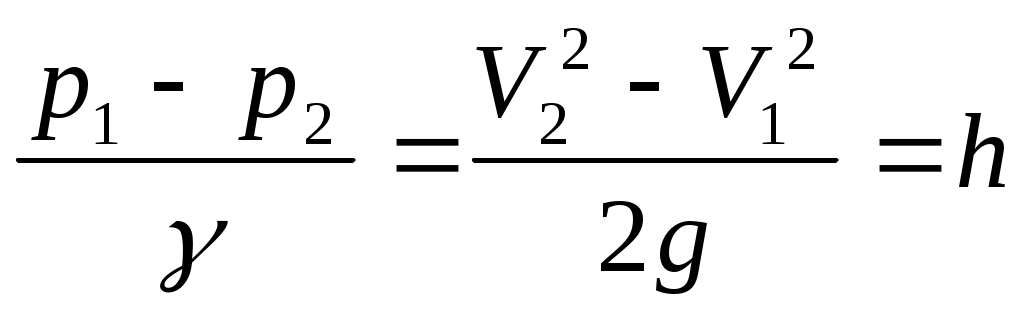
Здесь h – разность уровней в пьезометрических трубках
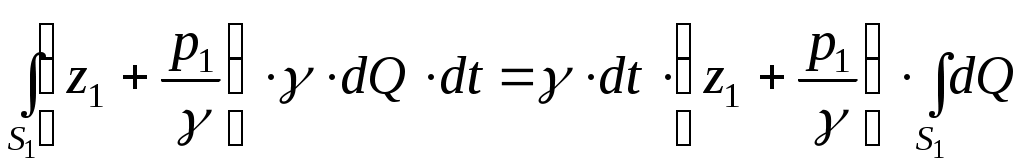 .
.Но
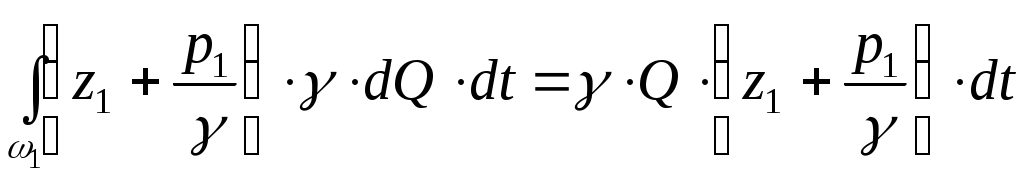 . (II.21)
. (II.21)Запишем второй интеграл в следующем виде:
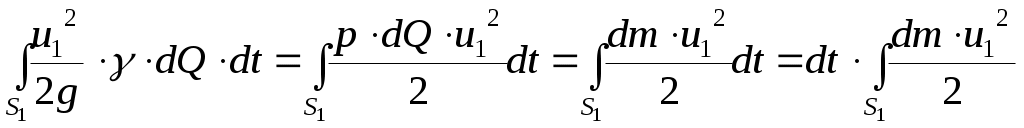
Этот интеграл представляет собой, как уже указывалось, кинетическую энергию, проносимую потоком через сечение 1-1 за время
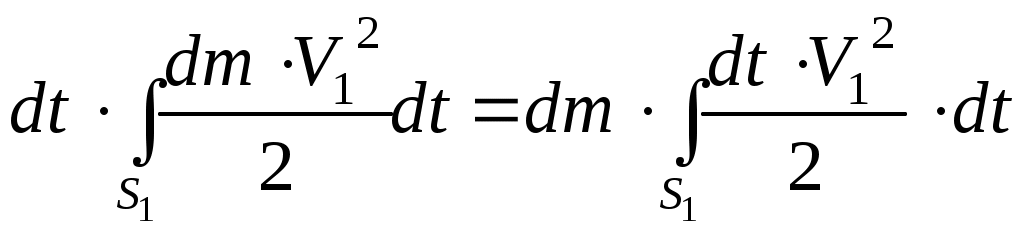 .
.Это выражение по величине всегда меньше, чем действительная кинетическая энергия, вычисленная по действительным скоростям. обозначим отношение этих двух величин
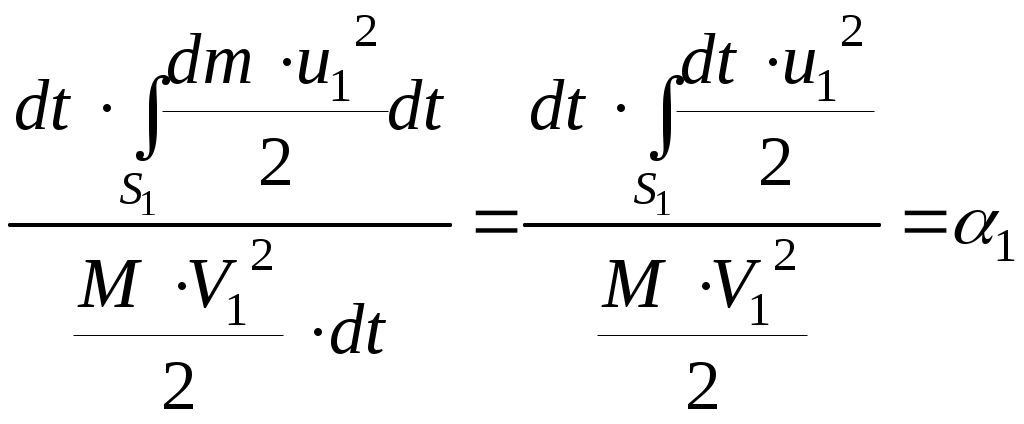 . (II.02)
. (II.02)Коэффициент
Возвращаясь к поставленной задаче о вычислении второго интеграла в выражении (11.20), констатируем, что его значение можно выразить через среднюю скорость посредством введения коэффициента кинетической энергии
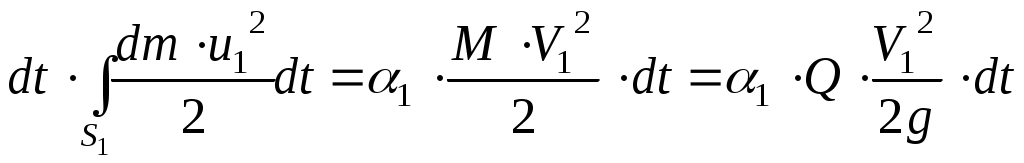
(II.23)
Подставив значения интегралов (11.21) и (11.23) в зависимость (11.20), получим:
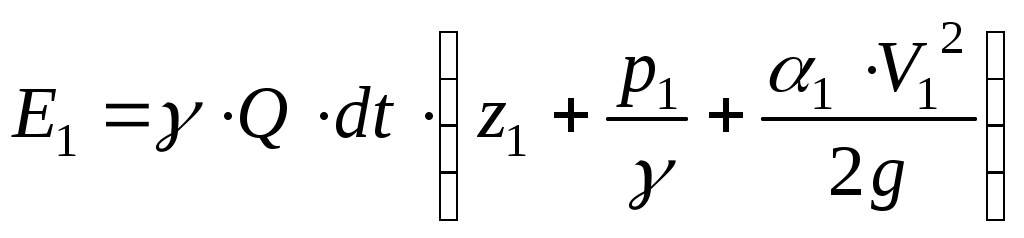 (II.24)
(II.24)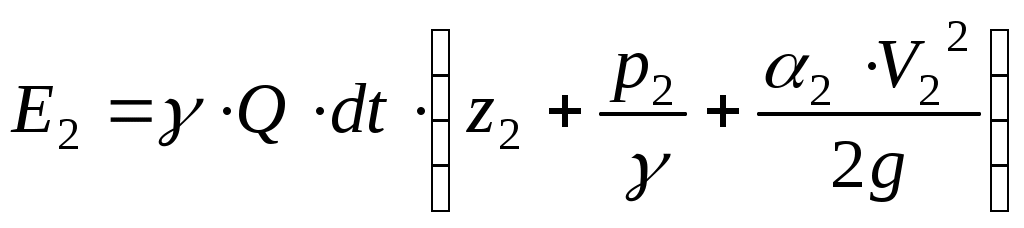 (II.25)
(II.25)Поделив выражения (11.24) и (11.25) на вес жидкости
Так как на участке потока между сечениями 1-1 и 2-2 часть энергии потока затрачивается на преодоление гидравлических сопротивлений и необратимо превращается в тепловую энергию,
Тогда:
или
Полученное уравнение и есть уравнение Д.Бернулли для установившегося потока реальной жидкости. По внешнему виду оно почти не отличается от полученного ранее уравнения Бернулли для элементарной струйки реальной жидкости. Тем не менее это уравнение обладает рядом отличительных особенностей, которые необходимо всегда помнить для правильного его использования.
Во-первых, это уравнение записывается не для отдельных частиц жидкости, находящихся на одной и той же линии тока, а для различных сечений потока, при этом совершенно различно, какую частицу жидкости в сечении мы выбираем для определения величин
Во-вторых, не обязательно, чтобы поток на всем протяжении между рассматриваемыми сечениями, для которых составляется уравнение Д.Бернулли, был близким к параллельноструйчатому. На этом участке он может претерпевать весьма резкие изменения своей формы. Совершенно необходимо лишь, чтобы в сечениях, для которых записывается уравнение Д.Бернулли, движение было плавно изменяющимся.
Изменение формы (деформация) потока сопровождается затратами удельной его энергии и учитывается членом
По аналогии с предыдущим будем называть величину
Отметим, что при равномерном движении, когда
Практическое использование уравнения Д.Бернулли
«Уравнение Бернулли имеет чрезвычайно важное значение в гидравлике, позволяя по двум известным элементам их трех (
С помощью уравнения Бернулли легко объяснить ряд явлений, наблюдаемых в технике и повседневной жизни. Так, например, очень легко установить характер распределения давлений в горизонтальной трубе переменного сечения (рис. II.06). Действительно, применяя уравнение неразрывности к двум сечениям, показанным на рисунке, устанавливаем, что в узкой части поток обладает большими средними скоростями, чем в широкой части:
Запишем уравнение Бернулли для этих же сечений потока. Это воз
Отсюда найдем:
Но ранее было установлено, что

Рис. II.06.
Полученный результат подчеркивает специфическую особенность жидкостей преобразовывать кинетическую энергию давления (и наоборот), что очень хорошо используется в технике и находит самые разнообразные применения. Так, например, пропуская жидкость с большими скоростями через суженные сечения, можно значительно понизить в этом сечении давление и создать благоприятные условия для всасывания жидкости. Этот принцип используется для создания различных струйных аппаратов (водоструйных и пароструйных насосов и т.п.). Очень широко используется тот же принцип в измерительной технике для определения установившихся расходов жидкости и скоростей ее движения.
Рассмотрим так называемый водомер Вентури, который служит для измерения расхода жидкости и представляет собой короткий двухконусный патрубок, сначала суживающийся, а затем расширяющийся (рис. II.06.), вмонтированный в короткий трубопровод.
Записывая уравнение Бернули для сечений 1 и 2, получим при тех же предположениях, что и выше, зависимость (11.29), которую перепишем в виде:
Здесь h – разность уровней в пьезометрических трубках