Файл: Законов в технике. Тема I. Основы гидростатики.doc

2.5. Уравнение Д.Бернулли для элементарной струйки реальной жидкости. Пьезометрический и гидравлический уклоны
При движении реальной жидкости между соседними струйками возникают силы трения, на преодоление которых затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2-2 будет мене удельной энергии жидкости в сечении 1-1 на некоторую величину , которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом:

(11.14)

Следовательно, при установившемся движении реальной жидкости сумма четырех высот (геометрической, пьезометрической, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий 9положения, давления, кинетической и потерянной) не изменяется вдоль данной элементарной струйки.

Легко изобразить уравнение Бернулли для рассматриваемого случая графически. Для этого следует, выбрав произвольную горизонтальную плоскость сравнения, отложить на ней в каждом сечении высоты ; ; и . Концы отрезков , соединенные плавной кривой, покажут положение оси струйки. Соединяя концы отрезков плавной кривой, получим так называемую пьезометрическую линию. Отложив в каждом сечении вверх от пьезометрической линии отрезки, равные скоростным напорам , и соединив их концы плавной кривой, получим линию гидродинамического напора или, как ее часто называют, гидравлическую линию (рис. II.02). Отрезки, равные расстояниям по вертикали от гидравлической линии

---

, проходящей над плоскостью сравнения на высоте, равной начальной удельной энергии на гидравлические сопротивления на участке от начального до рассматриваемого сечения.



Рис. II.02
Проделаем теперь следующее построение: разверзнем криволинейную ось струйки s в горизонтальную прямую линию и в каждой ее точке отложим по вертикали значения удельных энергий ; и . Соединяя концы отрезков и , получим изображение пьезометрической и гидравлической линий. Падение пьезометрической линии на единицу длины элементарной струйки назовем пьезометрическим уклоном :

. (11.15)

Соответственно падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном I:

(11.16)

На графике (рис. II.03) пьезометрический уклон представляется тангенсом угла наклона касательной к пьезометрической линии, а гидравлический уклон – тангенсом угла наклона касательной к гидравлической линии. Значение пьезометрического уклона может быть положительным или отрицательным в зависимости от того, увеличивается или уменьшается величина удельной потенциальной энергии вдоль элементарной струйки.



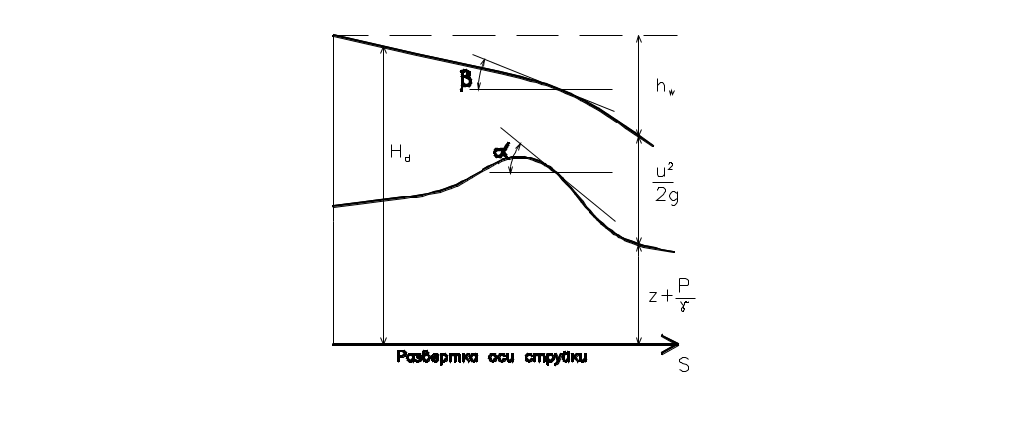
Рис. II.03
Гидравлиеческий уклон есть всегда величина положительная, так как полная удельная энергия движущейся части жидкости постепенно уменьшается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в тепловую энергию и рассеиваясь.

---

2.6. Понятие о плавно изменяющемся (медленно изменяющемся) движении потока жидкости
В общем случае при установившемся движении поток жидкости можно представить совокупностью элементарных струек, имеющих различные значения углов их расхождения и различные радиусы кривизны. Частный случай движения потока, при котором он испытывает слабую деформацию, так что элементарные струйки остаются параллельными или почти параллельными друг другу , а радиусы их кривизны принимают весьма большие значения , называется плавно изменяющимся или медленно изменяющимся движением. Живые сечения потока при плавно изменяющемся движении, очевидно, будут весьма мало отличаться от плоских сечений, поэтому их приближенно можно считать плоскими. Скорости движения всех частиц жидкости в таких сечениях направлены параллельно друг другу и нормально к плоскости живого сечения. Отметим, что часто поток жидкости имеет плавно изменяющееся движение не на всем своем протяжении, а лишь на некоторых участках. Так, например поток жидкости, изображенный на рис. II.04, в живом сечении 1-1 имеет плавно изменяющееся движение, а в сечении 2-2 претерпевает значительную деформацию.

Выясним, какими свойствами обладает плавно изменяющееся движение потока жидкости. Для этого запишем дифференциальные уравнения реальной капельной жидкости. Так как реальная жидкость обладает вязкостью, которая приводит к возникновению в жидкости при ее движении сил трения, необходимо к дифференциальным уравнениям движения идеальной жидкости (Л.Эйлера) добавить член, учитывающий эти силы.

Выберем оси координат так, чтобы направление х совпало с направлением вектора скорости u. В случае установившегося плавно изменяющегося движения будем иметь:

; ; .

---

Рис. II.04
Силы трения совпадают по направлению с вектором скорости, поэтому они спроектируются на ось х в истинную величину, а на оси y и z дадут нулевые проекции. С учетом сказанного запишем: член, учитывающий силы трения = ;

; . (11.17)

Добавим уравнение неразрывности:

.

Из уравнения неразрывности следует, что

(т.к. ).

Из определения установившегося движения следует, что . Но с учетом этого получим:

;

; .

Перепишем уравнения (11.37) в следующем виде:

член, учитывающий силы трения = 0;

; . (11.18)

Уравнения (11.18) определяют закон распределения гидродинамического давления в потоке при плавно изменяющемся установившемся движении. Вторая и третья строчки этой системы уравнений определяют закон распределения гидродинамического давления в плоскости zoy, то есть в плоскости живого сечения потока. Легко заметить, что они ничем не отличаются от соответствующих строк дифференциального уравнения гидростатики (1.5). Отсюда можно сделать вывод, что в плоскости живого сечения потока при плавно изменяющемся движении гидродинамические давления распределяются по законам гидростатики, а это значит, что в данном живом сечении удельная потенциальная энергия любой частицы есть величина постоянная:

---

. (11.19)

Сразу же оговоримся, что в другом живом сечении потока жидкости, где движение будет плавно изменяющимся, все частицы жидкости также будут обладать одинаковой удельной потенциальной энергией, но эта энергия может быть отличной от энергии частиц в первом живом сечении.
2.7. Уравнение Д.Бернулли для потока реальной жидкости.

Условия применимости уравнения Д.Бернулли
Распространим уравнение Бернулли на установившийся поток реальной жидкости. Для этого выберем на слабо деформированном участке потока живое сечение, вблизи которого движение можно считать плавноизменяющимся ( например, сечение 1-1 на рис. II.05).



Рис. II.05
Через это сечение каждой элементарной струйкой за время dt вносится энергия, которая в соответсвии с вышеизложенным оказывается равной:

.

Учитывая, что , и вынося за скобки все жидкости, прошедший через поперечное сечение элементарной струйки за время dt, равный , перепишем это выражение в следующем виде:

.

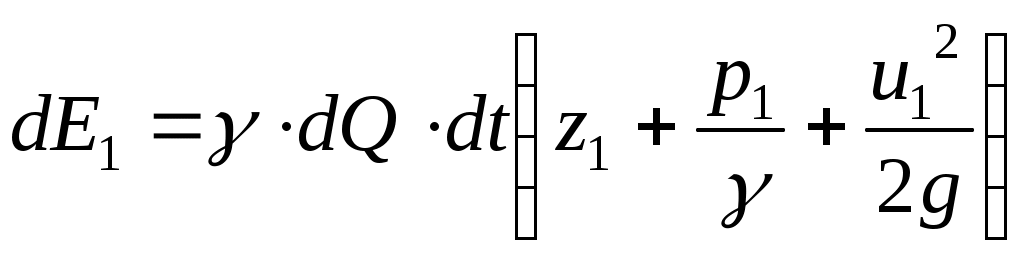Найдем полную энергию, проносимую потоком жидкости через живое сечение 1-1. для этого необходимо, очевидно, просуммировать полученное выражение по всем струйкам данного живого сечения.

Тогда получим:



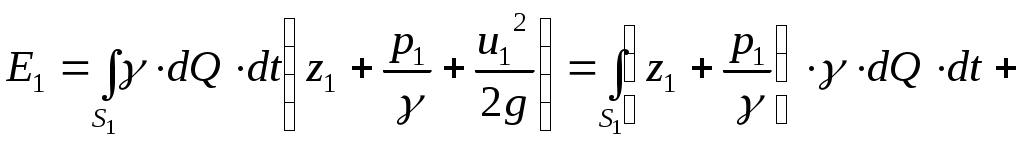
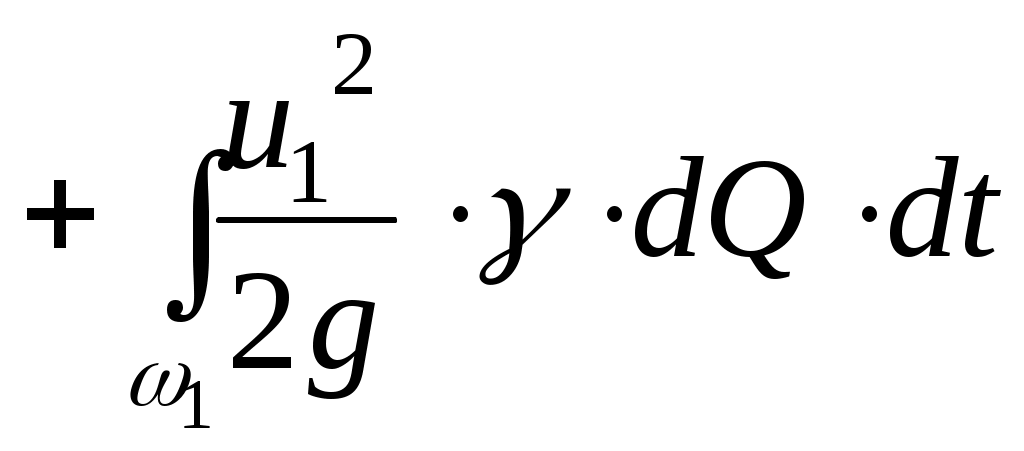(11.20)

Таким образом, полная энергия Е₁ оказывается равной сумме двух интегралов, представляющих собой соответственно потенциальную и кинетическую энергию потока.

Вычислим первый интеграл. Так как в сечении 1-1 величина (см. зависимость 11.19), ее можно вынести за знак интеграла точно так же, как и

---