Файл: Audio and Radio Engineering.pdf

1-26 Principles of Sound and Hearing

quency rising), the sound level at the receiver will decline from the maximum level in the
approach to the first destructive interference at 

λ/2 = r

2

 – r

1

, where the level drops to a null. Con-

tinuing upward in frequency, the sound level at the receiver rises to the original level when 

λ = r

2

– r

1

, falls to another null at 3

λ/2 = r

2

 – r

1

, rises again at 2

λ = r

2

 – r

1

, and so on, alternating

between maxima and minima at regular intervals in the frequency domain. The plot of the fre-
quency response of such a transmission path is called an interference pattern. It has the visual
appearance of a comb, and the phenomenon has also come to be called comb filtering (see Figure
1.2.2b).

Taking a more general view and considering the effects averaged over a range of frequencies,

it is possible to generalize as follows for the influence of a single reflecting surface on the sound
level due to the direct sound alone [2].

•

When r

2

 – r

1

is much less than a wavelength, the sound level at the receiver will be elevated

by 6 dB or less, depending on the surface absorption and distances involved.

•

When r

2

 – r

1

is approximately equal to a wavelength, the sound level at the receiver will be

elevated between 3 and 6 dB, depending on the specific circumstances.

•

When r

2

 – r

1

is much greater than a wavelength, the sound level at the receiver will be ele-

vated by between 0 and 3 dB, depending on the surface absorption and distances involved.

A special case occurs when the sound source, such as a loudspeaker, is mounted in the reflecting
plane itself. There is no path length difference, and the source radiates into a hemisphere of free
space, more commonly called a half space, or 2

π sr. The sound level at the receiver is then ele-

vated by 6 dB at frequencies where the sound source is truly omnidirectional, which—in prac-
tice—is only at low frequencies.

Other reflecting surfaces contribute additively to the elevation of the sound level at the

receiver in amounts that can be arrived at by independent analysis of each. Consider the situation
in which a simple point monopole (omnidirectional) source of sound is progressively constrained
by reflecting planes intersecting at right angles. In practice this could be the boundaries of a
room that are immediately adjacent to a loudspeaker which, at very low frequencies, is effec-
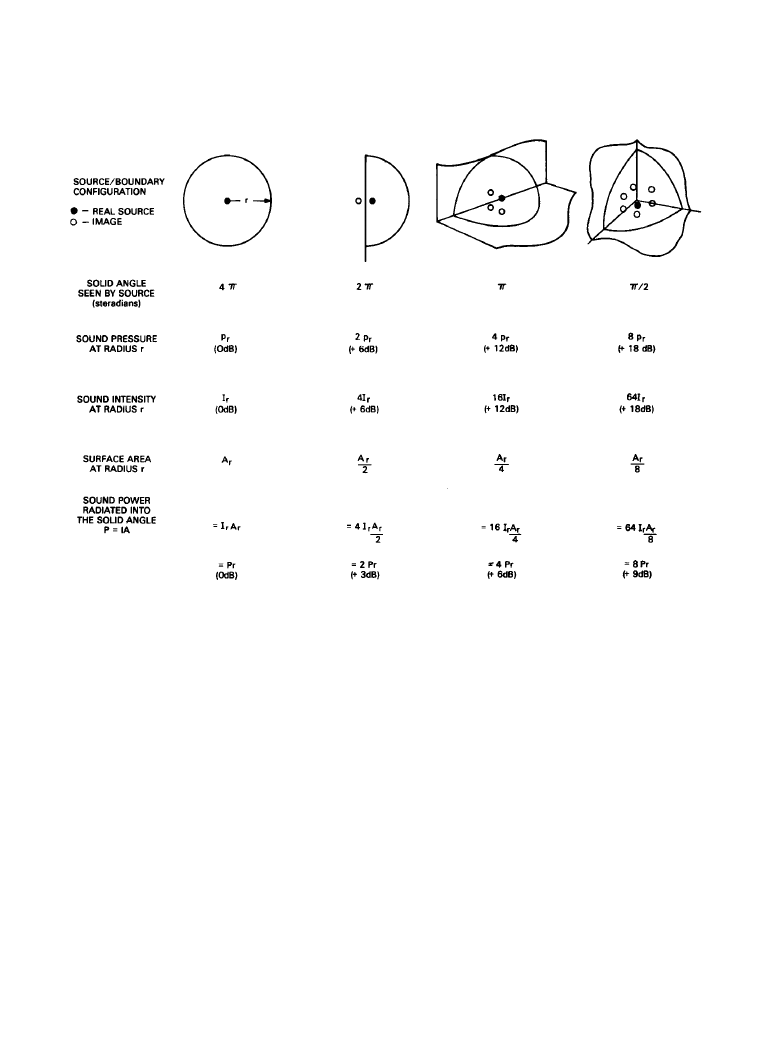
tively an omnidirectional source of sound. Figure 1.2.3 summarizes the relationships between
four common circumstances, where the sound output from the source radiates into solid angles
that reduce in stages by a factor of 2. These correspond to a loudspeaker radiating into free space
(4

π sr), placed against a large reflecting surface (2π sr), placed at the intersection of two reflect-

ing surfaces (

π sr), and placed at the intersection of three reflecting surfaces (π/2 sr). In all cases

the dimensions of the source and its distance from any of the reflecting surfaces are assumed to
be a small fraction of a wavelength. The source is also assumed to produce a constant volume
velocity of sound output; i.e., the volumetric rate of air movement is constant throughout.

By using the principles outlined here and combining the outputs from the appropriate number

of image sources that are acoustically mirrored in the reflective surfaces, it is found that the
sound pressure at a given radius increases in inverse proportion to the reduction in solid angle;
sound pressure increases by a factor of 2, or 6 dB, for each halving of the solid angle.

The corresponding sound intensity (the sound power passing through a unit surface area of a

sphere of the given radius) is proportional to pressure squared. Sound intensity therefore
increases by a factor of 4 for each halving of the solid angle. This also is 6 dB for each reduction
in angle because the quantity is power rather than pressure.

Finally, multiplying the sound intensity by the surface area at the given radius yields the total

sound power radiated into the solid angle. Because the surface area at each transition is reduced

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

Sound Propagation 1-27

by a factor of 2, the total sound power radiated into the solid angle increases by a factor of 2, or 3
dB, for each halving of the solid angle.

By applying the reverse logic, reducing the solid angle by half increases the rate of energy

flow into the solid angle by a factor of 2. At a given radius, this energy flows through half of the
surface area that it previously did, so that the sound intensity is increased by a factor of 4; i.e.,
pressure squared is increased by a factor of 4. This means that sound pressure at that same radius
is increased by a factor of 2.

The simplicity of this argument applies when the surfaces shown in Figure 1.2.3 are the only

ones present; this can only happen outdoors. In rooms there are the other boundaries to consider,
and the predictions discussed here will be modified by the reflections, absorption, and standing-
wave patterns therein.

Figure 1.2.3

 Behavior of a point monopole sound source in full space (4

π

) and in close proximity

to reflecting surfaces that constrain the sound radiation to progressively smaller solid angeles.
(

After [3].)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

1-28 Principles of Sound and Hearing

1.2.3b

Diffraction

The leakage of sound energy around the edges of an opening or around the corners of an obstacle
results in a bending of the sound rays and a distortion of the wave-front. The effect is called dif-
fraction. Because of diffraction it is possible to hear sounds around corners and behind walls-
anywhere there might have been an “acoustical shadow.” In fact, acoustical shadows exist, but to
an extent that is dependent on the relationship between the wavelength and the dimensions of the
objects in the path of the sound waves.

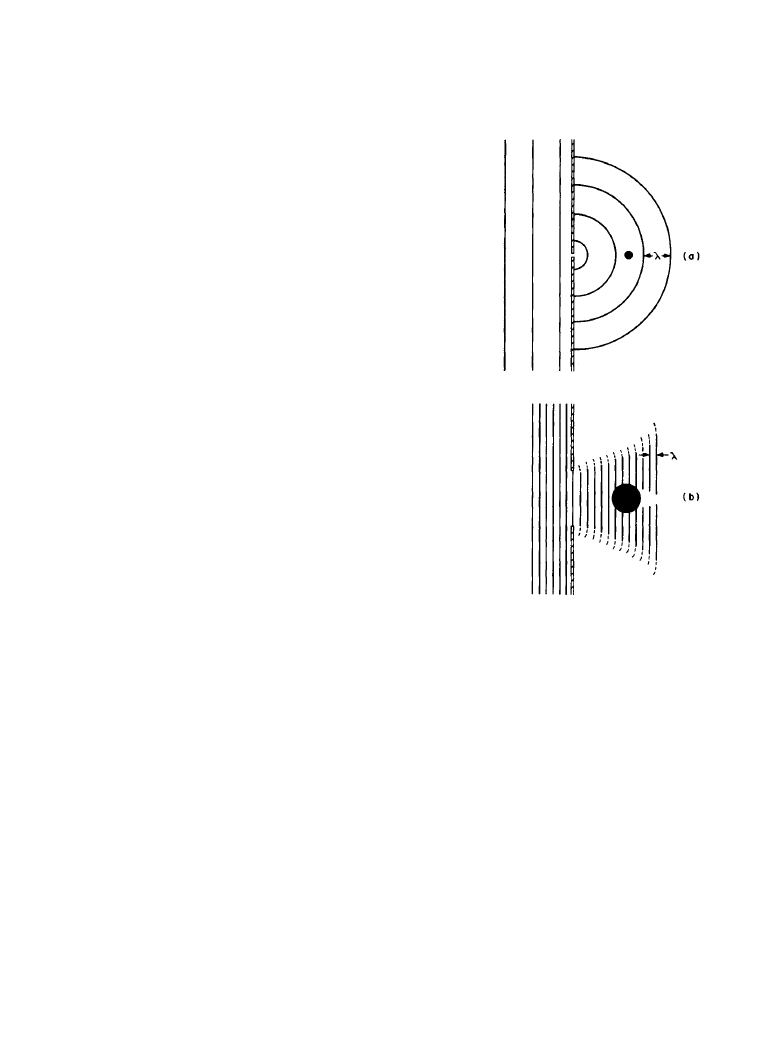
When the openings or obstructions are small compared with the wavelength of the sound, the

waves tend to spread in all directions and the shadowing effect is small. At higher frequencies,
when the openings or obstructions are large compared with the wavelengths, the sound waves
tend to continue in their original direction of travel and there is significant shadowing. Figure
1.2.4 illustrates the effect.

The principle is maintained if the openings are considered to be the diaphragms of loudspeak-

ers. If one wishes to maintain wide dispersion at all frequencies, the radiating areas of the driver
units must progressively reduce at higher frequencies. Conversely, large radiating areas can be
used to restrict the dispersion, though the dimensions required may become impractically large at

Figure 1.2.4 

Stylized illustration of the diffraction of sound

waves passing through openings and around obstacles. (

a)

The case where the wavelength is large compared with the
size of the opening and the obstacle. (

b) The case where

the wavelength is small compared with the size of the open-
ing and the obstacle.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

Sound Propagation 1-29

low frequencies. As a consequence, most loudspeakers are approximately omnidirectional at low
frequencies.

Sounds radiated by musical instruments obey the same laws. Low-frequency sounds from

most instruments and the human voice radiate in all directions. Higher-frequency components
can exhibit quite strong directional biases that are dependent on the size and orientation of the
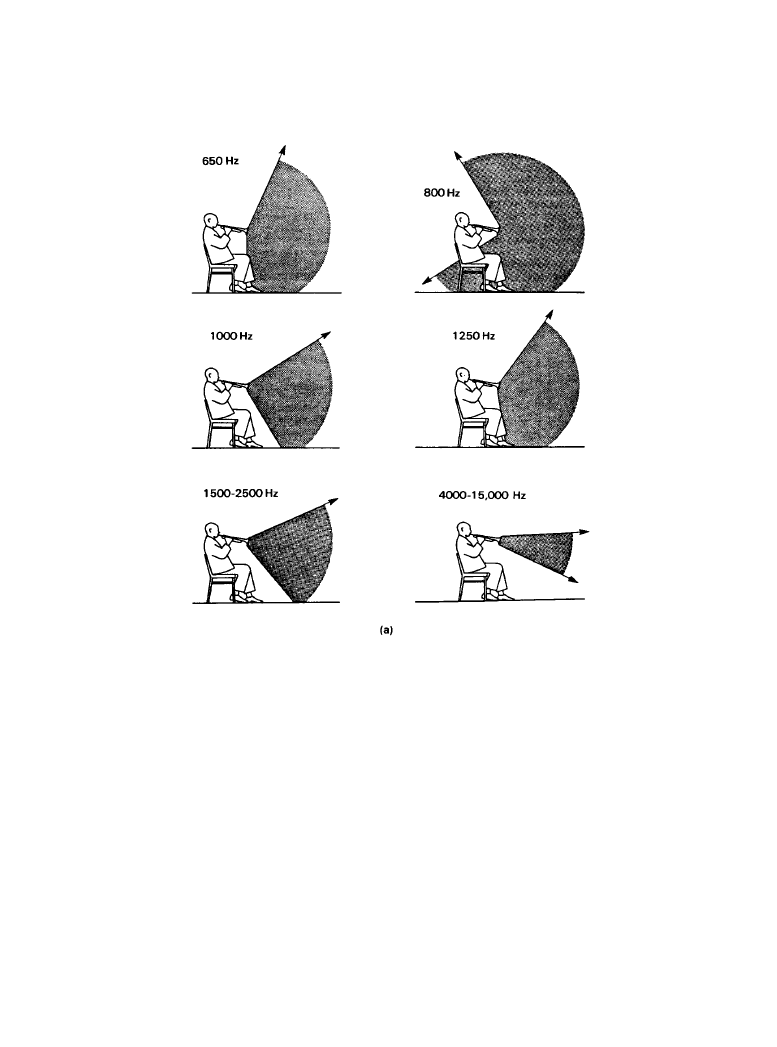
major sound-radiating elements. Figure 1.2.5a shows the frequency-dependent directivities of a
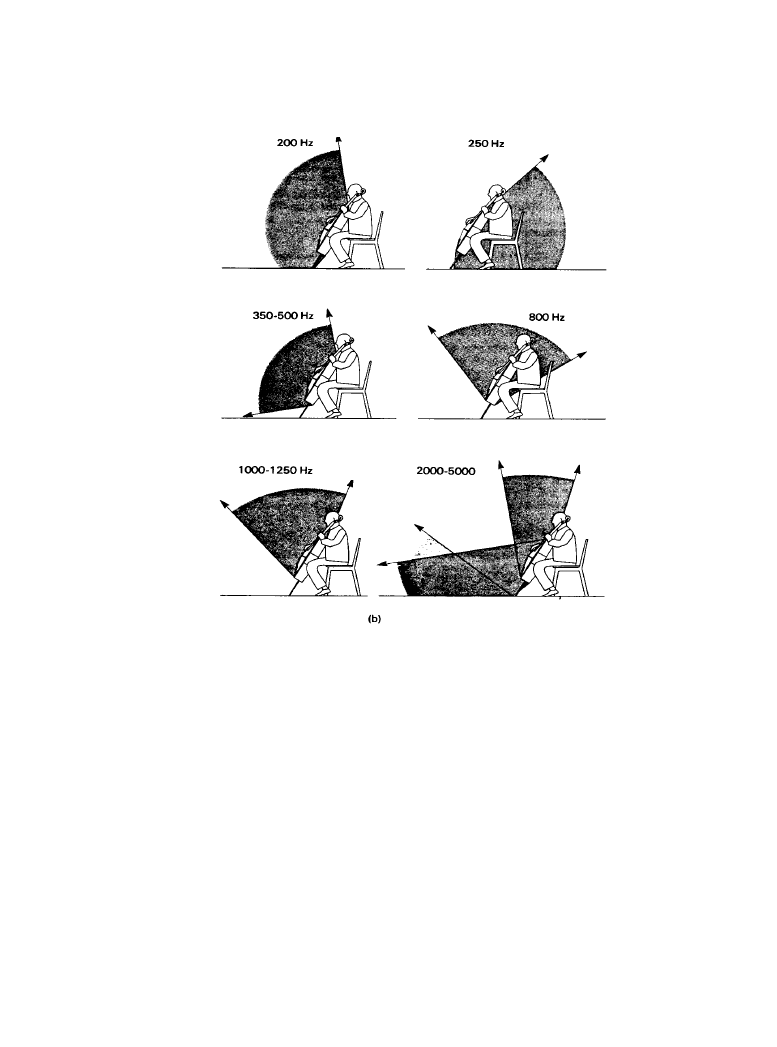
trumpet, a relatively simple source. Compare this with the complexity of the directional charac-
teristics of a cello (Figure 1.2.5b). It is clear that no single direction is representative of the total
sound output from complex sound sources—a particular difficulty when it comes to choosing
microphone locations for sound recordings. Listeners at a live performance hear a combination
of all the directional components as spatially integrated by the stage enclosure and the hall itself.

Figure 1.2.5

 A simplified display of the main sound radiation directions at selected frequencies

for: (

a) a trumpet, (b, next page) a cello. (From [4]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

1-30 Principles of Sound and Hearing

1.2.3c

Refraction

Sound travels faster in warm air than in cold and faster downwind than upwind. These factors
can cause sound rays to be bent, or refracted, when propagating over long distances in vertical
gradients of wind or temperature. Figure 1.2.6 shows the downward refraction of sound when the
propagation is downwind or in a temperature inversion, as occurs at night when the temperature
near the ground is cooler than the air higher up. Upward refraction occurs when the propagation
is upwind or in a temperature lapse, a typical daytime condition when the air temperature falls
with increasing altitude. Thus, the ability to hear sounds over long distances is a function of local
climatic conditions; the success of outdoor sound events can be significantly affected by the time
of day and the direction of prevailing winds.

Figure 1.2.5

b

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation