Файл: Audio and Radio Engineering.pdf

Sound Propagation 1-31

1.2.4

References

1.

Piercy, J. E., and T. F. W. Embleton: “Sound Propagation in the Open Air,” in Handbook of
Noise Control, 2d ed., C. M. Harris (ed.), McGraw-Hill, New York, N.Y., 1979.

2.

Waterhouse, R. V., and C. M. Harris: “Sound in Enclosed Spaces,” in Handbook of Noise
Control, 2d ed., C. M. Harris (ed.), McGraw-Hill, New York, N.Y., 1979.

3.

Olson, Harry F.: Acoustical Engineering, Van Nostrand, New York, N.Y., 1957.

4.

Meyer, J.: Acoustics and the Performance of Music, Verlag das Musikinstrument, Frankfurt
am Main, 1987.

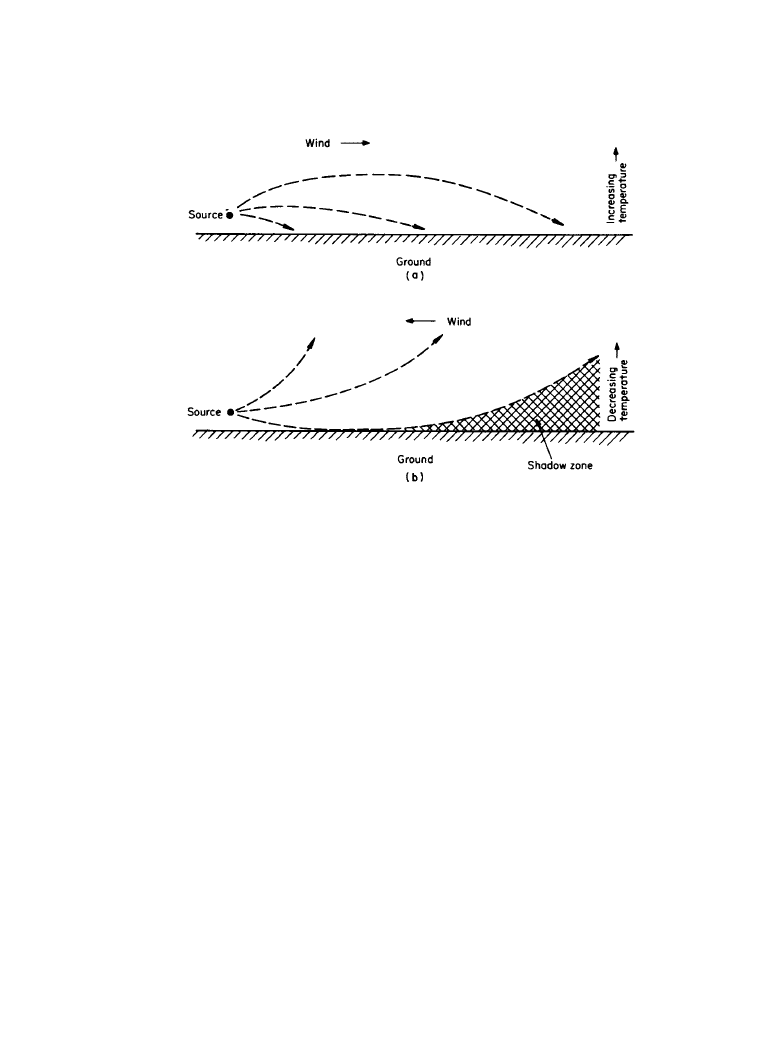
Figure 1.2.6

 The refraction of sound by wind and by temperature gradients: (

a) downwind or in a

temperature inversion, (

b) upwind or in a temperature lapse. (From [1]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Sound Propagation

1-33

Chapter

1.3

Resonance

Floyd E. Toole

E. A. G. Shaw, G. A. Daigle, M. R. Stinson

1.3.1

Introduction

A vibrating system of any kind that is driven by and is completely under the control of an exter-
nal source of energy is in a state of forced vibration. The activity within such a system after the
external force has been removed is known as free vibration. In this condition most systems
exhibit a tendency to move at a natural or resonant frequency, declining with time at a rate deter-
mined by the amount of energy dissipation, or damping, in the system. The resonances in some
musical instruments have little damping, as the devices are intended to resonate and produce
sound at specific frequencies in response to inputs, such as impacts or turbulent airflow, that do
not have any specific frequency characteristics. Most instruments provide the musician with
some control over the damping so that the duration of the notes can be varied.

1.3.2

Fundamental Properties

If the frequency of the driving force is matched to the natural frequency of the resonant system,
the magnitude of the vibration and the efficiency of the energy transfer are maximized.

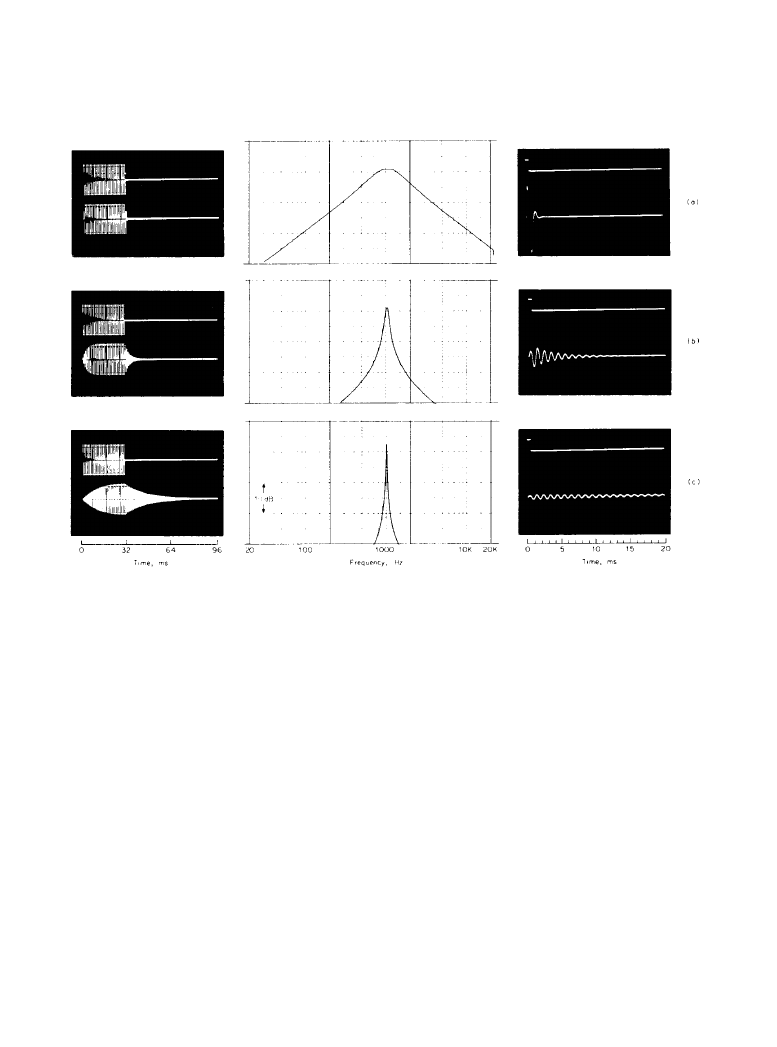
These and other points are illustrated in Figure 1.3.1, which shows three versions of a reso-

nant system having different amounts of damping. The term commonly used to describe this
characteristic of resonant systems is the quality factor, Q, a measure of the lightness of damping
in a system. The system in Figure 1.3.1a has a Q of 1; it is well damped. The system in Figure
1.3.1b is less welt damped and has a Q of 10, while that in Figure 1.3.1c has little damping and is
described as having a Q of 50. As a practical example, the resonance of a loudspeaker in an
enclosure would typically have a Q of 1 or less. Panel resonances in enclosures might have Qs in
the region of 10 or so. Resonances with a Q of 50 or more would be rare in sound reproducers
but common in musical instruments.

On the left in Figure 1.3.1 can be seen the behavior of these systems when they are forced into

oscillation by a pure tone tuned to the resonance frequency of the systems, 1000 Hz. When the

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Source: Standard Handbook of Audio and Radio Engineering

1-34 Principles of Sound and Hearing

tone is turned on and off, the systems respond with a speed that is in inverse proportion to the Q.
The low-Q resonance responds quickly to the onset of the tone and terminates its activity with
equal brevity. The medium-Q system responds at a more leisurely rate and lets the activity decay
at a similar rate after the cessation of the driving signal. The high-Q system is slow to respond to
the driving signal and sustains the activity for some time after the interval of forced oscillation.

In the preceding example the forcing signal was optimized in frequency, in that it matched the

resonance frequency of the system, and it was sustained long enough for the system to reach its
level of maximum response. On the right of Figure 1.3.1 are shown the responses of these sys-
tems to an impulse signal brief in the time domain but having energy over a wide range of fre-
quencies including that of the resonant system. In Figure 1.3.1a the low-Q system is shown
responding energetically to this signal but demonstrating little sustained activity. In Figure 1.3.1b
and 1.3.1c the higher-Q systems respond with progressively reduced amplitude but with progres-
sively sustained ringing alter the pulse has ended. Note that the ringing is recognizably at the res-
onance frequency, 1 cycle/ms.

Figure 1.3.1 

The frequency responses of three resonant systems and their behavior in conditions

of forced and free vibration. The system show in (

a) has the least damping (Q = 1), system (b) has

moderate damping (

Q = 10), and the system shown in (c) has the least damping (Q = 50).

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance

Resonance 1-35

In the center of Figure 1.3.1 are shown the amplitude-frequency responses or, more com-

monly, the frequency responses of the systems. These curves show the amplitude of system
response when the frequency of a constant driving signal is varied from well below the resonance
frequency to well above it. The low-Q system Figure 1.3.1a is seen to respond to signals over a
wide frequency range, but the higher-Q systems become progressively more frequency-selective.

In this illustration, the maximum amplitudes of the system responses at resonance were

adjusted to be approximately equal. Such is often the case in electronic resonators used in filters,
frequency equalizers, synthesizers, and similar devices. In simple resonant systems in which
everything else is held equal and only the damping is varied, the maximum amplitude response
would be highest in the system with the least dissipation: the high-Q system, Figure 1.3.1c. Add-
ing damping to the system would reduce the maximum amplitude, so that the system with the
lowest Q, having the highest damping or losses, would respond to the widest range of frequen-
cies, but with reduced amplitude [1].

Figure 1.3.2 shows the frequency responses of two systems with multiple resonances. In

1.3.2a the resonances are such that they respond independently to driving forces at single fre-
quencies. In 1.3.2b an input at any single frequency would cause some activity in all the resona-
tors but at different amplitudes in each one. The series of high-Q resonators in Figure 1.3.2a is
characteristic of musical instruments, where the purpose is the efficient production of sound at
highly specific frequencies. The overlapping set of low-Q resonators in Figure 1.3.2b are the fil-
ters of a parametric equalizer in which the frequency, Q, and amplitude of the filters are individ-
ually adjustable to provide a variable overall frequency response for a sound-recording or sound-
reproducing system.

A special case of Figure 1.3.2b would be a multiway loudspeaker system intended for the

reproduction of sounds of all kinds. In this case, the selection of loudspeaker units and their asso-
ciated filters (crossovers) would be such that, in combination, they resulted in an overall ampli-
tude response that is flat (the same at all frequencies) over the required frequency range. Such a
system would be capable of accurately recreating any signal spectrum. For the loudspeaker or
any system of multiple filters or resonant elements to accurately pass or reproduce a complex
waveform, there must be no phase shift at the important frequencies. In technical terms this
would be assessed by the phase-frequency response, or phase response, of the system showing
the amount of phase shift at frequencies within the system bandwidth.

Resonant systems can take any of several forms of electrical, mechanical, or acoustical ele-

ments or combinations thereof. In electronics, resonators are the basis for frequency-selective or
tuned circuits of all kinds, from radios to equalizers and music synthesizers. Mechanical reso-
nances are the essential pitch determinants of tuning forks, bells, xylophones, and glockenspiels.
Acoustical resonances are the essential tuning devices of organs and other wind instruments.
Stringed instruments involve combinations of mechanical and acoustical resonances in the gen-
eration and processing of their sounds, as do reed instruments and the human voice.

The voice is a good example of a complex resonant system. The sound originates as a train of

pulses emanating from the voice box. This excites a set of resonances in the vocal tract so that
the sound output from the mouth is emphasized at certain frequencies. In spectral terms, the
envelope of the line spectrum is modified by the frequency response of the resonators in the
vocal tract. These resonances are called formants, and their frequencies contribute to the individ-
ual character of voices. The relative amplitudes of the resonances are altered by changing the
physical form of the vocal tract so as to create different vowel sounds, as illustrated in Figure
1.3.3 [2–4].

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance