Файл: Audio and Radio Engineering.pdf

1-36 Principles of Sound and Hearing

1.3.2a

Resonance in Pipes

When the diameter of a pipe is small compared with the wavelength, sound will travel as plane
waves perpendicular to the length of the pipe. At a closed end the sound is reflected back down
the pipe in the reverse direction. At an open end, some of the sound radiates outward and the
remainder is reflected backward, but with a pressure reversal (180° phase shift). The pressure
distribution along the pipe is therefore the sum of several sound waves traveling backward and
forward. At most frequencies the summation of these several waves results in varying degrees of
destructive interference, but at some specific frequencies the interference is only constructive
and a pattern stabilizes in the form of standing waves. At these frequencies, the wavelengths of
the sounds are such that specific end conditions of the tube are simultaneously met by the waves
traveling in both directions, the sounds reinforce each other, and a resonant condition exists.

Figures 1.3.4 and 1.3.5 show the first three resonant modes for pipes open at both ends and

for those with one end closed. The open ends prevent the pressures from building up, but the par-

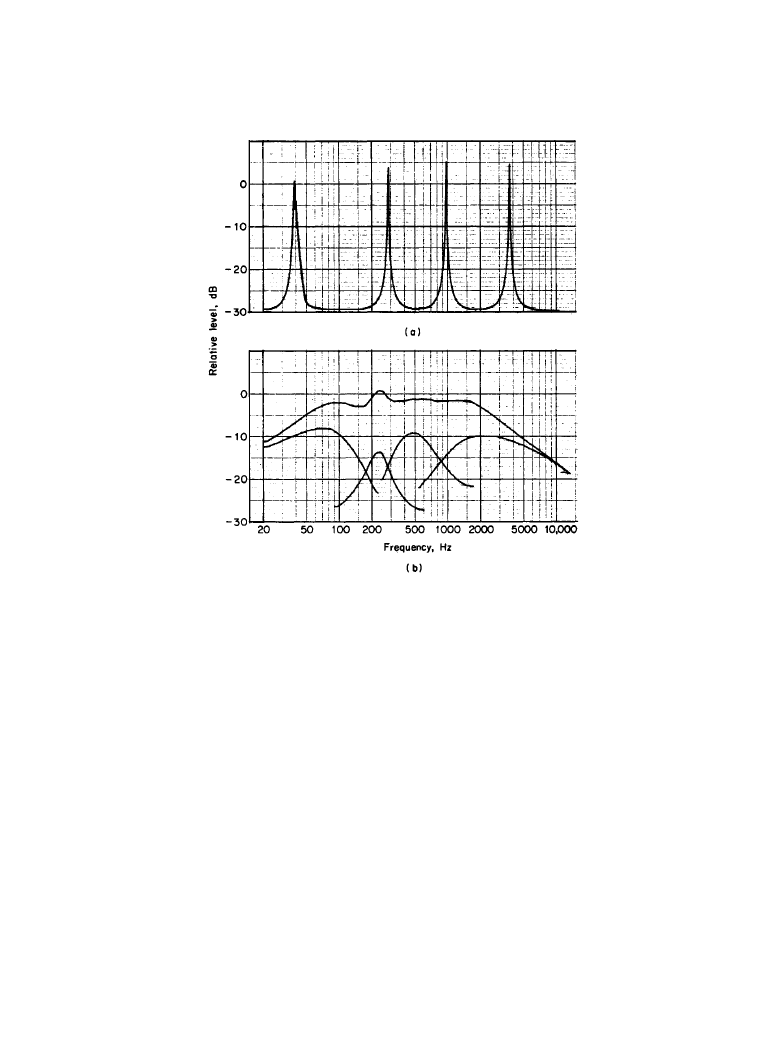
Figure 1.3.2 

Two systems with multiple resonances: (

a) well-separated high-Q resonances that

can respond nearly independently of each other, as in the notes of a musical instrument; (

b) the

four filters of a parametric equalizer designed to produce overlapping low-

Q resonance curves

(bottom traces) which are combined to produce a total response (top trace) that may bear little
resemblance to the individual contributions.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance

Resonance 1-37

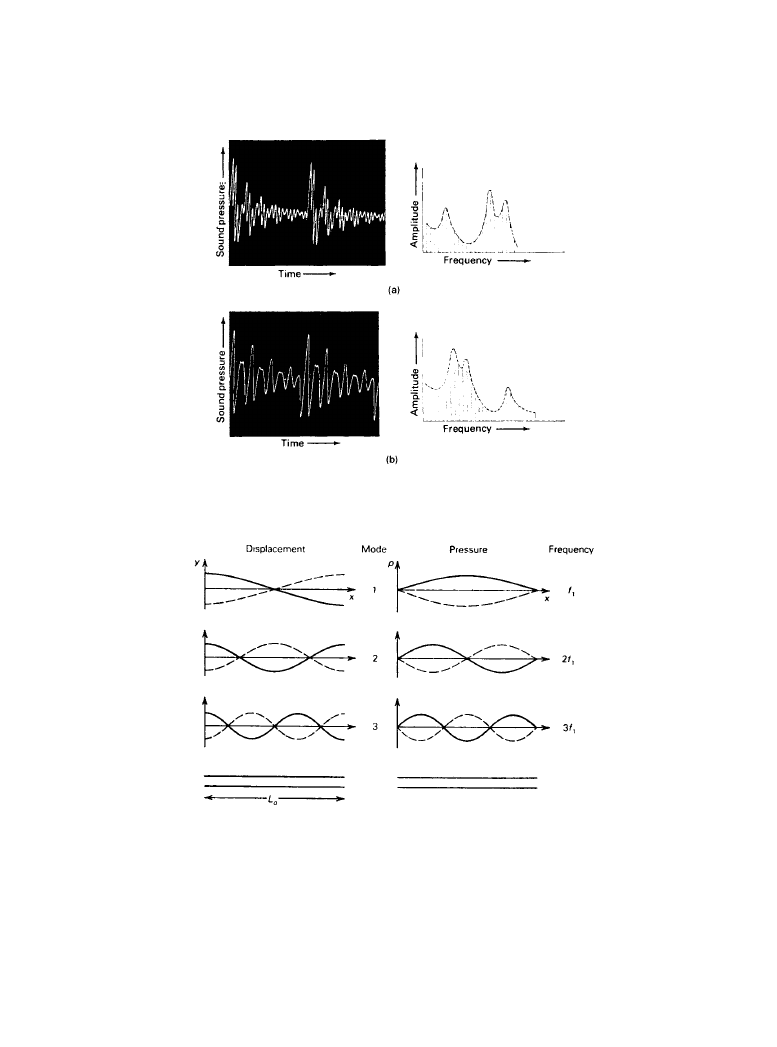
Figure 1.3.3

 The waveforms and corresponding amplitude-frequency spectra of the vowel sounds

“uh” (

a) and “ah” (b). (From [3]. Used with permission.)

Figure 1.3.4

 The first three resonant modes of air in a tube open at both ends. On the left are the

patterns of particle displacement along the tube, showing the antinodes at the ends of the tube. At
the right are the corresponding patterns of pressure, with the required nodes at the ends. The fun-
damental frequency is 

c/2L

o

. (

From [7]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance

1-38 Principles of Sound and Hearing

ticle displacements are unimpeded; the end condition for resonance is therefore a displacement
maximum (antinode) and a pressure minimum (node) in the standing-wave pattern. A closed end
does the reverse, forcing displacements to zero but permitting pressure to build up; the end con-
dition for resonance is therefore a displacement node and a pressure antinode.

For a pipe open at both ends, the fundamental frequency has a wavelength that is double the

length of the pipe; conversely, the pipe is one-half wavelength long. The fundamental frequency
is therefore f = c/2L

o

, where L is the length of the pipe in meters and c is the speed of sound: 345

m/s. Other resonances occur at all harmonically related frequencies: 2f

1

, 3f

1

, and so on.

A pipe closed at one end is one-quarter wavelength long at the fundamental resonance fre-

quency; thus f = c/4L

c

. In this case, however, the other resonances occur at odd harmonics only:

3f

1

, 5f

1

, and so on. A very simplistic view of the vocal tract considers it as a pipe, closed at the

vocal cords, open at the mouth, and 175 mm long [4]. This yields a fundamental frequency of
about 500 Hz and harmonics at 1500, 2500, and 3500 Hz. These are close to the formant fre-
quencies appearing as resonance humps in the spectra of Figure 1.3.3.

Organ pipes are of both forms, although the pipes open at both ends produce the musically

richer sound. To save space, pipes closed at one end are sometimes used for the lowest notes;
these need be only one-fourth wavelength long, but they produce only odd harmonics.

In practice this simple theory must be modified slightly to account for what is called the end

correction. This can be interpreted as the distance beyond the open end of the pipe over which
the plane waves traveling down the pipe make the transition to spherical wavefronts as they
diverge after passing beyond the constraints of the pipe walls. The pipe behaves as it is longer
than its physical length by an amount equal to 0.62 times its radius. If the pipe has a flange or
opens onto a flat surface, the end correction is 0.82 times the radius.

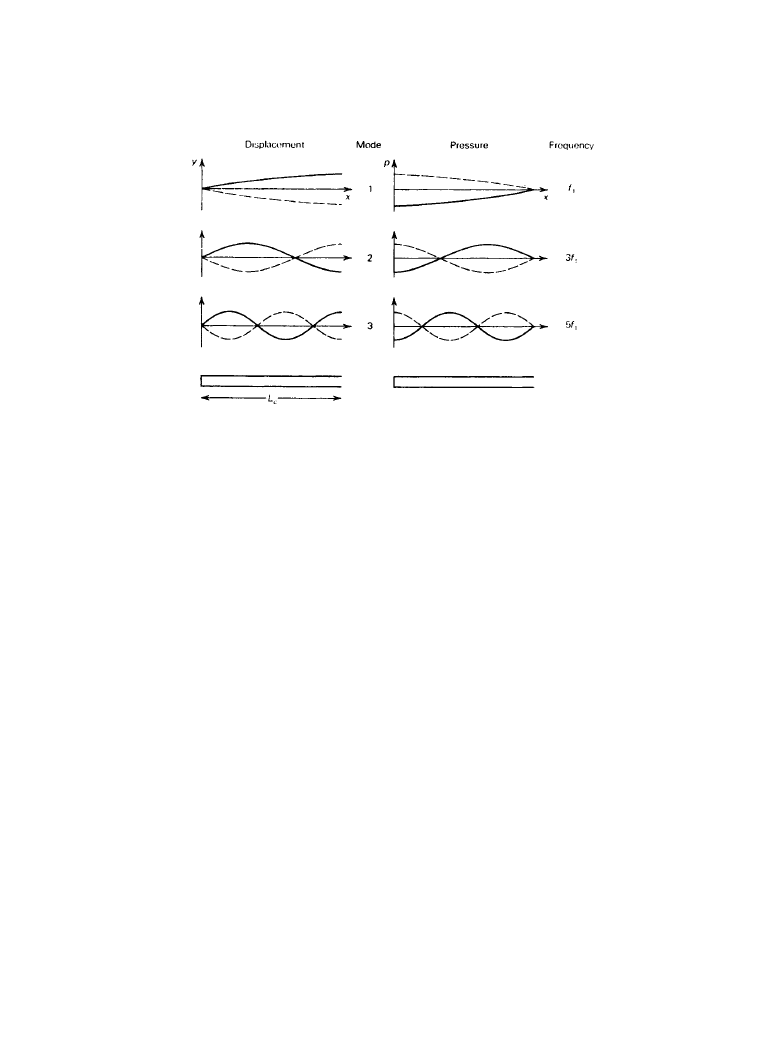
Figure 1.3.5

 The first three resonant modes of air in a tube closed at one end. On the left are the

patterns of particle displacement along the tube, and on the right are the pressure distributions.
The fundamental frequency is 

c/4L

o

. (

From [7]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance

Resonance 1-39

1.3.2b

Resonance in Rooms and Large Enclosures

Sounds propagating in rectangular rooms and large enclosures are subject to standing waves
between the reflecting boundaries. In taking a one-dimensional view for illustration, sounds
reflecting back and forth between two parallel surfaces form standing waves at frequencies satis-
fying the boundary conditions requiring pressure antinodes and particle displacement nodes at
the reflecting surfaces. The fundamental resonance frequency is that at which the separation is
one-half wavelength. Other resonances occur at harmonics of this frequency. This same phenom-
enon exists between all opposing pairs of parallel surfaces, establishing three sets of resonances,
dependent on the length, width, and height, known as the axial modes of the enclosure. Other
resonances are associated with sounds reflected from four surfaces and propagating in a plane
parallel to the remaining two. For example, sound can be reflected from the four walls and travel
parallel to the floor and ceiling. The three sets of these resonances are called tangential modes.
Finally, there are resonances involving sounds reflected from all surfaces in the enclosure, called
oblique modes. All these resonant modes, or eigentones, can be calculated from the following
equation

(1.3.1)

where:
f

n

 = frequency of the nth mode

n

x

, n

y

, n

z

 = integers with independently chosen values between 0 and 

∞

l

x

, l

y

, l

z

 = dimensions of enclosure, m (ft)

c = speed of sound, m/s (ft/s)

It is customary to identify the individual modes by a combination of n

x

, n

y

, and n

z

, as in (2, 0,

0), which identifies the mode as being the second-harmonic resonance along the x dimension of
the enclosure. All axial modes are described by a single integer and two zeros. Tangential modes
are identified by two integers and one zero, and oblique modes by three integers. The calculation
of all modes for an enclosure would require the calculation of Equation (1.3.1) for all possible
combinations of integers for n

x

, n

y

, and n

z

.

The sound field inside an enclosure is therefore a complex combination of many modes, and

after the sound input has been terminated, they can decay at quite different rates depending on
the amount and distribution of acoustical absorption on the room boundaries. Because some
energy is lost at every reflection, the modes that interact most frequently with the room bound-
aries will decay first. The oblique modes have the shortest average distance between reflections
and are the first to decay, followed by the tangential modes and later by the axial modes. This
means that the sound field in a room is very complex immediately following the cessation of
sound production, and it rapidly deteriorates to a few energetic tangential and axial modes [5, 6].

The ratio of length to width to height of an enclosure determines the distribution of the reso-

nant modes in the frequency domain. The dimensions themselves determine the frequencies of
the modes. The efficiency with which the sound source and receiver couple to the various modes
determines the relative influence of the modes in the transmission of sound from the source to
the receiver. These factors are important in the design of enclosures for specific purposes. In a
listening or control room, for example, the locations of the loudspeakers and listeners are largely

f

n

c
2

---

n

x

l

x

-----

 

 

 

2

n

y

l

y

-----

 

 

2

n

z

l

z

-----

 

 

2

+

+

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance

1-40 Principles of Sound and Hearing

determined by the geometrical requirements for good stereo listening and by restrictions
imposed by the loudspeaker design. Accurate communication from the source to the receiver
over a range of frequencies requires that the influential room modes be uniformly distributed in
frequency. Clusters or gaps in the distribution of modes can cause sounds at some frequencies to
be accentuated and others to be attenuated, altering the frequency response of the sound propaga-
tion path through the room. This causes the timbre of sounds propagated through the room to be
changed.

Certain dimensional ratios have been promoted as having especially desirable mode distribu-

tions. Indeed, there are shapes like cubes and corridors that clearly present problems, but the
selection of an ideal rectangular enclosure must accommodate the particular requirements of the
application. Generalizations based on the simple application of Equation (1.3.1) assume that the
boundaries of the enclosure are perfectly reflecting and flat, that all modes are equally energetic,
and that the source and receiver are equally well coupled to them all. In practice it is highly
improbable that these conditions will be met.

1.3.2c

Resonance in Small Enclosures: Helmholtz Resonators

At frequencies where the wavelength is large compared with the interior dimensions of an enclo-
sure, there is negligible wave motion because the sound pressure is nearly uniform throughout
the volume. In these circumstances the lumped-element properties of the enclosed air dominate,
and another form of resonance assumes control. Such Helmholtz resonators form an important
class of acoustic resonators.

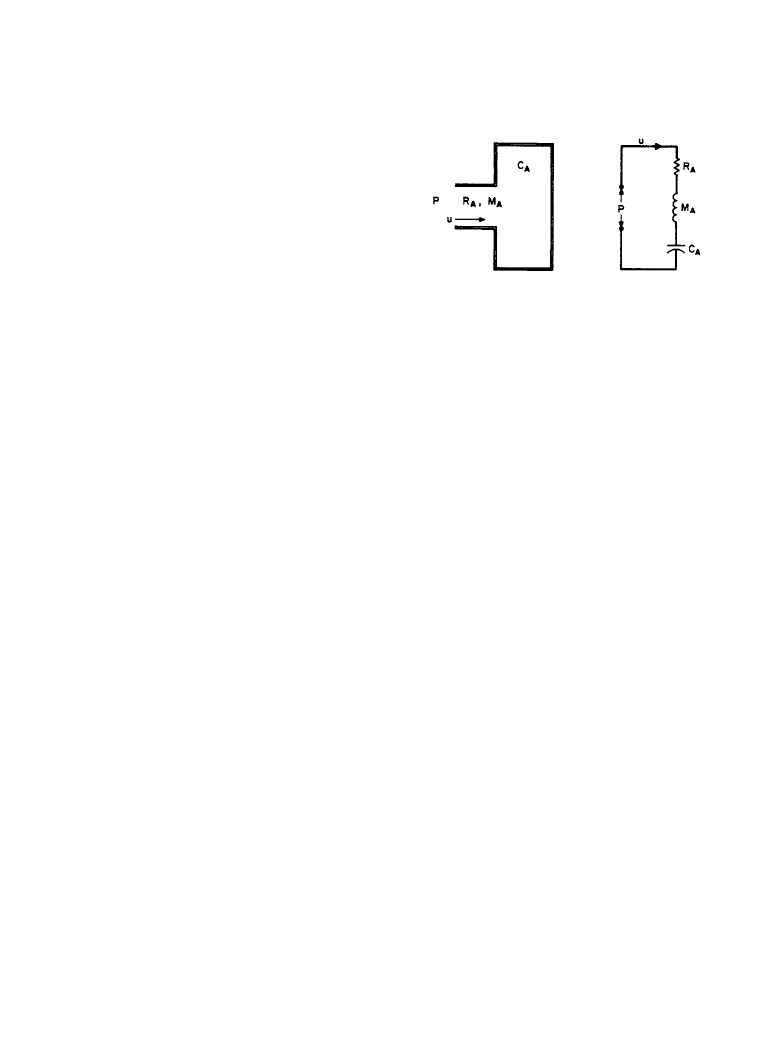
Figure 1.3.6 shows a simple cavity with a short ducted opening, like a bottle with a neck. Here

the volume of air within the cavity acts as a spring for the mass of air in the neck, and the system
behaves as the acoustical version of a mechanical spring-mass resonant system. It is also analo-
gous to the electrical resonant circuit with elements as shown in the figure.

Acoustical compliance increases with the volume, meaning that the resonance frequency falls

with increasing cavity volume. The acoustic mass (inertance) in the duct increases with the
length of the duct and decreases with increasing duct area, leading to a resonance frequency that
is proportional to the square root of the duct area and inversely proportional to the square root of
the duct length.

Helmholtz resonators are the simplest form of resonating systems. They are found as the air

resonance in the body of guitars, violins, and similar instruments, and they are the principal fre-
quency-determining mechanism in whistles and ocarinas. They also describe the performance of
loudspeaker-enclosure systems at low frequencies. The acoustical-mechanical-electrical analogs
introduced here are the basis for the design of closed-box and reflex loudspeaker systems, result-

Figure 1.3.6

 Physical representation of a

Helmholtz resonator (left) and the correspond-
ing symbolic representation as a series reso-
nant acoustical circuit (right). Legend: 

P  =

sound pressure at mouth; 

µ

 = volume velocity

at the port = particle velocity 

×

 port area; 

R

A

 =

acoustical resistance; 

M

A

 = acoustical mass of

the port; 

C

A

 = acoustical compliance of the vol-

umne.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Resonance