Файл: Audio Power Amp Design Handbook.pdf

The output stage I

so. Using my design methodology a Blameless amplifier can be straightfor-
wardly designed to produce less than 0.0006% THD at 10 Hz (150 W/8 !)
without  even  considering  thermal  distortion;  this  suggests  that  we  have
here a non-problem.

I accept that it is not uncommon to see amplifier THD plots that rise at low
frequencies; but whenever I have been able to investigate this, the LF rise
could  be  eliminated  by  attending  to  either  defective  decoupling  or
feedback-capacitor distortion. Any thermal distortion must be at a very low
level as it is invisible at 0.0006%; remember that this is the level of a THD
reading that is visually pure noise, though there are real amplifier distortion
products buried in it.

I have therefore done some deeper investigation by spectrum analysis of
the residual, which enables the harmonics to be extracted from the noise.
The test amplifier was an optimally-biased Class-B machine very similar to
that  on  Figure  6.16,  except  with  a  CFP  output.  The  Audio  Precision
oscillator is very, very clean but this amplifier tests it to its limits, and so
Table 5.5 below shows harmonics in a before-and-after-amplifier compar-
ison.  The  spectrum  analyser  bandwidth  was  1 Hz  for  10 Hz  tests,  and
4.5 Hz for 1 kHz, to discriminate against wideband noise.

This further peeling of the distortion onion shows several things; that the AP is
a brilliant piece of machinery, and that the amplifier is really quite linear too.
However there is nothing resembling evidence for thermal distortion effects.

As  a  final  argument,  consider  the  distortion  residual  of  a  slightly
underbiased power-amp, using a CFP output configuration so that output

155

Table 5.5 Relative amplitute of distortion harmonics

10 Hz AP out · · · · Amp out

1 kHz AP out · · · · Amp out

Fundamental

.00013%

.00031%

.00012%

.00035%

Second

.00033%

.00092%

.00008%

.00060%

Third

.00035%

.00050%

.000013%

.00024%

Fourth

<.000002%

.00035%

<.000008%

.00048%

Fifth

<.00025%

<.00045%

.000014%

.00024%

Sixth

<.000006%

.00030%

.000008%

.00021%

Seventh

<.000006%

<.00008%

.000009%

.00009%

Eighth

<.000003%

.00003%

.000008%

.00016%

Ninth

<.000004%

.00011%

.000007%

<.00008%

AP THD reading
(80 kHz bandwidth)

.00046%

.00095%

.00060%

.00117%

NB: The rejection of the fundamental is not perfect, and this is shown as it contributes to the THD figure.

Audio Power Amplifier Design Handbook

device  junction  temperatures  do  not  affect  the  quiescent  current;  it
therefore depends only on the driver temperatures. When the amplifier is
switched on and begins to apply sinewave power to a load, the crossover
spikes  (generated  by  the  deliberate  underbiasing)  will  be  seen  to  slowly
shrink  in  height  over  a  couple  of  minutes  as  the  drivers  warm  up.  This
occurs even with the usual temperature compensation system, because of
the delays and losses in heating up the Vbe-multiplier transistor.

The size of these crossover spikes gives in effect a continuous readout of
driver  temperature,  and  the  slow  variations  that  are  seen  imply  time-
constants measured in tens of seconds or more; this must mean a negligible
response at 10 Hz.

There is no doubt that long-term thermal effects can alter Class-B amplifier
distortion,  because  as  I  have  written  elsewhere,  the  quiescent  current
setting is critical for the lowest possible high-frequency THD. However this
is  strictly  a  slow  (several  minutes)  phenomenon,  whereas  enthusiasts  for
thermal distortion are thinking of the usual sort of per-cycle distortion.

The above arguments lead me to conclude that thermal distortion as usually
described does not exist at a detectable level.

Thermal distortion in a power amp IC

Audio  writers  sometimes  speculate  about  ‘thermal  distortion’.  This  is
assumed to be caused by cyclic temperature changes at signal frequency,
causing  modulation  of  transistor  parameters.  It  is  undoubtedly  a  real
problem  in  power  ICs,  which  have  input  and  output  devices  in  close
thermal  proximity  on  the  same  piece  of  sillcon,  but  in  a  discrete-
component power amplifier there is no such thermal coupling, and no such
distortion.

Thermal  non-linearities  would  presumably  appear  as  second  or  third
harmonic distortion rising at low frequencies, and the largest effects should
be in Class-B output stages where dissipation varies greatly over a cycle.
There is absolutely no such effect to be seen in discrete-component power
amplifiers.

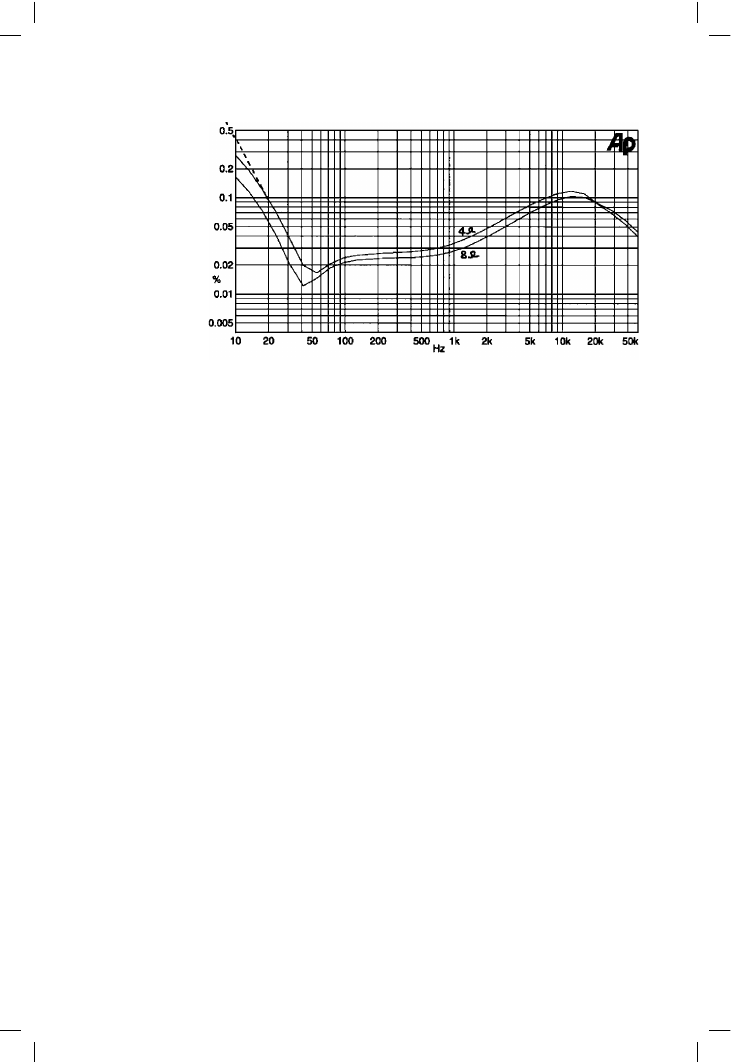
But thermal distortion certainly does exist in IC power amplifiers. Figure
5.47 is a distortion plot for the Philips TDA 1522Q power amp IC, which
I believe shows the effect. The power level was 4.4 W into 8 !, 8 W into
4 !.  As  is  usual  for  such  amplifiers,  the  distortion  is  generally  high,  but
drops  into  a  notch  at  40 Hz;  the  only  feasible  explanation  for  this  is
cancellation of distortion products from two separate distortion sources. At
frequencies below this notch there is second-harmonic distortion rising at
12 dB/octave as frequency falls. The LF residual looks quite different from
the midband distortion, which was a mixture of second and third harmonic
plus crossover spikes.

156

The output stage I

The  THD  figure  falls  above  10 kHz  because  of  the  80 kHz  bandwidth
limitation on the residual, and the high-order nature of the harmonics that
make up crossover distortion.

All  other  possible  sources  of  an  LF  distortion  rise,  such  as  inadequate
decoupling,  were  excluded.  There  was  no  output  capacitor  to  introduce
non-linearity.

It seems pretty clear that the steep rise here is due to thermal distortion, in
the  form of feedback from the power output stage to earlier parts of the
amplifier – probably the input stage. As would be expected, the effect is
greater with a heavier load which causes more heating; in fact halving the
load doubles the THD reading below the 40 Hz notch.

Selecting an output stage

Even if we stick to the most conventional of output stages, there are still an
embarrassingly large number to choose form. The cost of a complementary
pair of power FETs is currently at least twice that of roughly equivalent BJTs,
and taken with the poor linearity and low efficiency of these devices, the
use of them may require a marketing rather than a technical motivation.

Turning to BJTs, I conclude that there are the following candidates for Best
Output Stage:

1 the  Emitter-Follower  Type  II  output  stage  is  the  best  at  coping  with

switchoff  distortion  but  the  quiescent-current  stability  may  be
doubtful,

2 the  CFP  topology  has  good  quiescent  stability  and  low  LSN;  its  worst

drawback  is  that  reverse-biasing  the  output  bases  for  fast  switchoff  is
impossible without additional HT rails,

3 the  quasi-complementary-with-Baxandall-diode  stage  comes  close  to

mimicking the EF-type stages in linearity, with a potential for cost-saving
on output devices. Quiescent stability is not as good as the CFP.

157

Figure 5.47

Distortion plot for the
Phllips TDA1522Q
IC. Power out was
4.4 W rms into 8 !,
8 W rms into 4 !. The
dotted line shows a
12 dB/octave slope

Audio Power Amplifier Design Handbook

Closing the loop: distortion in complete amplifiers

In Chapter 4 it was shown how relatively simple design rules could ensure
that the THD of the small-signal stages alone could be reduced to less than
0.001%  across  the  audio  band,  in  a  thoroughly  repeatable  fashion,  and
without  using  frightening  amounts  of  negative  feedback.  Combining  this
sub-system with one of the more linear output stages described in Chapter
4,  such  as  the  CFP  version  which  gives  0.014%  THD  open-loop,  and
bearing  in  mind  that  ample  NFB  is  available,  it  seems  we  have  all  the
ingredients  for  a  virtually  distortionless  power  amplifier.  However,  life  is
rarely so simple . . .

(Note – the AP plots in Figures 5.5–5.7 were taken at 100 W rms into 8 !,
from an amplifier with an input error of –70 dB at 10 kHz and a c/l gain of
27 dB, giving a feedback factor of 43 dB at this frequency. This is well above
the dominant-pole frequency and so the NFB factor is dropping at 6 dB/
octave and will be down to 37 dB at 20 kHz. My experience suggests that
this is about as much feedback as is safe for general hi-fi usage, assuming
an  output  inductor  to  improve  stability  with  capacitative  loads.  Sadly,
published data on this touchy topic seems to be non-existent).

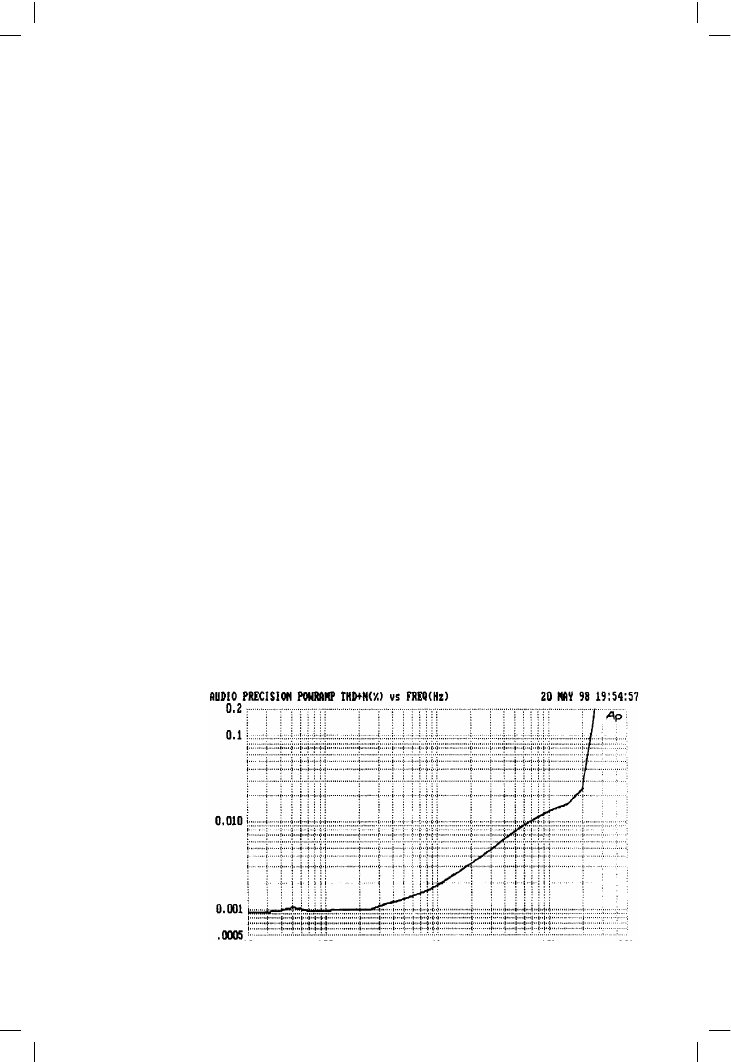
Figure  5.48  shows  the  distortion  performance  of  such  a  closed-loop
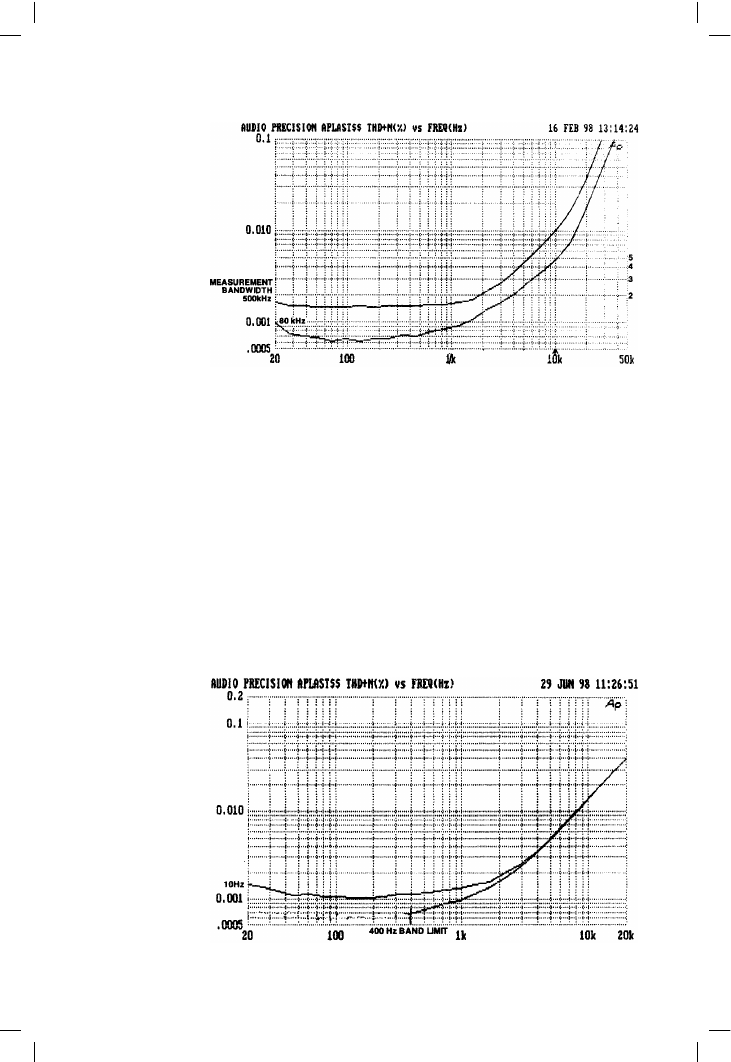
amplifier with an EF output stage, Figure 5.49 showing the same with a CFP
output stage. Figure 5.50 shows the THD of a quasi-complementary stage
with  Baxandall  diode

[14]

.  In  each  case  Distortion  1,  Distortion  2  and

Distortion 4–Distortion 7 have been eliminated, by methods described in
past and future chapters, to make the amplifier Blameless.

It will be seen at once that these amplifiers are not distortionless, though
the performance is markedly superior to the usual run of hardware. THD
in the LF region is very low, well below a noise floor of 0.0007%, and the
usual  rise  below  100 Hz  is  very  small  indeed.  However,  above  2 kHz,

158

Figure 5.48

Closed-loop amplifier
performance with
Emitter-Follower output
stage. 100 W into
8 !

The output stage I

THD  rises  with  frequency  at  between  6  and  12 dB/octave,  and  the
distortion residual in this region is clearly time-aligned with the crossover
region, and consists of high-order harmonics rather than second or third.
It is intriguing to note that the quasi-Bax output gives about the same HF
THD as the EF topology, which confirms the statement on page 119 that
the addition of a Baxandall diode essentially turns a conventional quasi-
complementary stage with serious crossover asymmetry into a reasonable
emulation  of  a  complementary  EF  stage.  There  is  less  HF  THD  with  a
CFP  output;  this  cannot  be  due  to  large-signal  non-linearity  as  this  is
negligible with an 8 ! load for all three stages, and so it must be due to
high-order  crossover  products.

The distortion figures given in this book are rather lower than usual. I would
like to emphasise that these are not freakish or unrepeatable figures; they

159

Figure 5.49

Closed-loop amplifier
performance with
CFP output. 100 W
into 8 !

Figure 5.50

Closed-loop amplifier
performance; quasi-
complementary
output stage with
Baxandall diode.
100 W into 8 !