Файл: Audio Power Amp Design Handbook.pdf

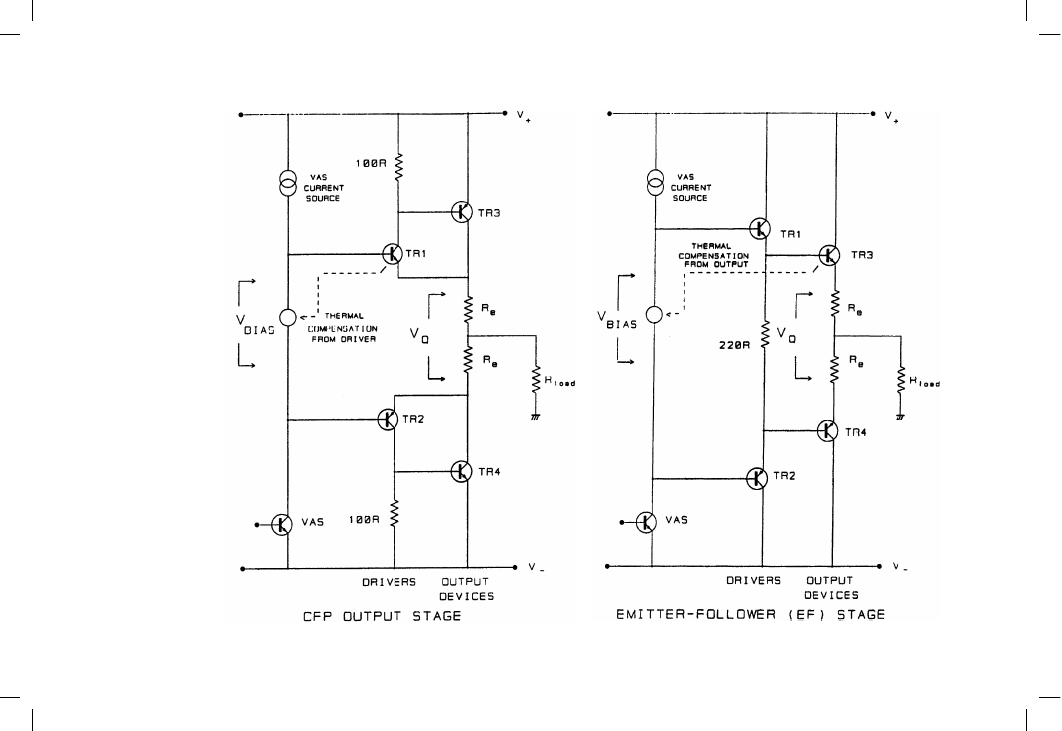
Figure 12.2

The Emitter-Follower
(EF) and
Complementary
Feedback Pair
(CFP) output
configurations,
showing Vbias and
Vq

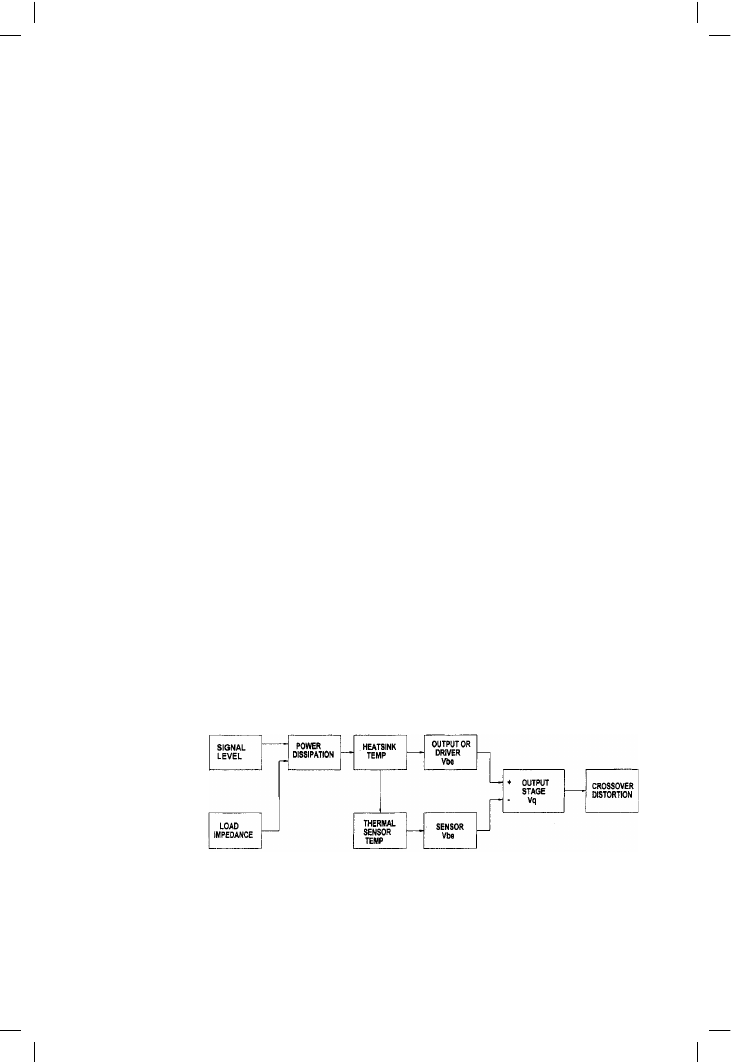
Thermal compensation and thermal dynamics

however CFP driver dissipation varies strongly with power output so the
superiority of this configuration cannot be taken for granted.

Driver heatsinks are much smaller than those for output devices, so the CFP
Vq time-constants promise to be some ten times shorter.

Basic thermal compensation

In Class B, the usual method for reducing quiescent variations is thermal
feedback.  Vbias  is  generated  by  a  thermal  sensor  with  a  negative
temperature-coefficient, usually a Vbe-multiplier transistor mounted on the
main heatsink. This system has proved entirely workable over the last 30-odd
years, and usually prevents any possibility of thermal runaway. However, it
suffers  from  thermal  losses  and  delays  between  output  devices  and
temperature  sensor  that  make  maintenance  of  optimal  bias  rather  ques-
tionable, and in practice quiescent conditions are a function of recent signal
and thermal history. Thus the crossover linearity of most power amplifiers is
intimately bound up with their thermal dynamics, and it is surprising this
area has not been examined more closely; Sato et al

[1]

is one of the few

serious papers on the subject, though the conclusions it reaches appear to be
unworkable,  depending  on  calculating  power  dissipation  from  amplifier
output voltage without considering load impedance.

As is almost routine in audio design, things are not as they appear. So-called
thermal feedback is not feedback at all – this implies the thermal sensor is
in some way controlling the output stage temperature; it is not. It is really
a form of approximate feedforward compensation, as shown in Figure 12.3.
The  quiescent  current  (Iq)  of  a  Class-B  design  causes  a  very  small
dissipation  compared  with  the  signal,  and  so  there  is  no  meaningful
feedback path returning from Iq to the left of the diagram. (This might be
less  true  of  Class-AB,  where  quiescent  dissipation  may  be  significant.)
Instead this system aspires to make the sensor junction temperature mimic
the  driver  or  output  junction  temperature,  though  it  can  never  do  this

331

Figure 12.3

Thermal signal flow
of a typical power
amplifier, showing
that there is no
thermal feedback to
the bias generator.
There is instead
feedforward of driver
junction temperature,
so that the sensor Vbe
will hopefully match
the driver Vbe

Audio Power Amplifier Design Handbook

promptly  or  exactly  because  of  the  thermal  resistances  and  thermal
capacities that lie between driver and sensor temperatures in Figure 12.3.
It  does  not  place  either  junction  temperature  or  quiescent  current  under
direct feedback control, but merely aims to cancel out the errors. Hereafter
I simply call this thermal compensation.

Assessing the bias errors

The temperature error must be converted to mV error in Vq, for comparison
with  the  tolerance  bands  suggested  above.  In  the  CFP  stage  this  is
straightforward; both driver Vbe and the halved Vbias voltage decrease by
2 mV per °C, so temperature error converts to voltage error by multiplying
by  .002  Only  half  of  each  output  stage  will  be  modelled,  exploiting
symmetry, so most of this chapter deals in half-Vq errors, etc. To minimise
confusion this use of half-amplifiers is adhered to throughout, except at the
final stage when the calculated Vq error is doubled before comparison with
the tolerance bands quoted above.

The EF error conversion is more subtle. The EF Vbias generator must establish
four times Vbe plus Vq, so the Vbe of the temperature-sensing transistor is
multiplied by about 4.5 times, and so decreases at 9 mV/°C. The CFP Vbias
generator only multiplies 2.1 times, decreasing at 4 mV/°C. The correspond-
ing values for a half-amplifier are 4.5 and 2 mV/°C.

However,  the  EF  drivers  are  at  near-constant  temperature,  so  after  two
driver  Vbe’s  have  been  subtracted  from  Vbias,  the  remaining  voltage
decreases faster with temperature than does output device Vbe. This runs
counter  to  the  tendency  to  under-compensation  caused  by  thermal
attenuation  between  output  junctions  and  thermal  sensor;  in  effect  the
compensator has thermal gain, and this has the potential to reduce long-
term Vq errors. I suspect this is the real reason why the EF stage, despite
looking unpromising, can in practice give acceptable quiescent stability.

Thermal simulation

Designing an output stage requires some appreciation of how effective the
thermal compensation will be, in terms of how much delay and attenuation
the  thermal  signal suffers  between  the  critical  junctions  and  the  Vbias
generator.

We need to predict the thermal behaviour of a heatsink assembly over time,
allowing for things like metals of dissimilar thermal conductivity, and the
very slow propagation of heat through a mass compared with near-instant
changes  in  electrical  dissipation.  Practical  measurements  are  very  time-
consuming, requiring special equipment such as multi-point thermocouple
recorders. A theoretical approach would be very useful.

332

Thermal compensation and thermal dynamics

For very simple models, such as heat flow down a uniform rod, we can
derive analytical solutions to the partial differential equations that describe
the  situation;  the  answer  is  an  equation  directly  relating  temperature  to
position along-the-rod and time. However, even slight complications (such
as a non-uniform rod) involve rapidly increasing mathematical complex-
ities, and anyone who is not already deterred should consult Carslaw and
Jaeger

[3]

; this will deter them.

To avoid direct confrontation with higher mathematics, finite-element and
relaxation  methods  were  developed;  the  snag  is  that  Finite-Element-
Analysis is a rather specialised taste, and so commercial FEA software is
expensive.

I  therefore  cast  about  for  another  method,  and  found  I  already  had  the
wherewithall to solve problems of thermal dynamics; the use of electrical
analogues  is  the  key.  If  the  thermal  problem  can  be  stated  in  terms  of
lumped electrical elements, then a circuit simulator of the SPICE type can
handle it, and as a bonus has extensive capabilities for graphical display of
the output. The work here was done with PSpice. A more common use of
electrical analogues is in the electro-mechanical domain of loudspeakers;
see Murphy

[4]

for a virtuoso example.

The simulation approach treats temperature as voltage, and thermal energy
as  electric  charge,  making  thermal  resistance  analogous  to  electrical
resistance,  and  thermal  capacity  to  electrical  capacitance.  Thermal
capacity is a measure of how much heat is required to raise the temperature
of a mass by 1°C. (And if anyone can work out what the thermal equivalent
of an inductor is, I would be interested to know.) With the right choice of
units the simulator output will be in Volts, with a one-to-one correspond-
ence with degrees Celsius, and Amps, similarly representing Watts of heat
flow; see Table 12.2. It is then simple to produce graphs of temperature
against time.

333

Table 12.2

Reality

Simulation

Temperature

°C

Volts

Heat quantity

Joules (Watt-seconds)

Coulombs (Amp-seconds)

Heat flowrate

Watts

Amps

Thermal resistance

°C/Watt

ohms

Thermal capacity

°C/Joule

Farads

Heat source

Dissipative element,

e.g. transistor

Current source

Ambient

Medium-sized planet

Voltage source

Audio Power Amplifier Design Handbook

Since heat flow is represented by current, the inputs to the simulated system
are current sources. A voltage source would force large chunks of metal to
change  temperature  instantly,  which  is  clearly  wrong.  The  ambient  is
modelled by a voltage source, as it can absorb any amount of heat without
changing temperature.

Modelling the EF output stage

The major characteristic of Emitter-Follower (EF) output stages is that the
output device junction temperatures are directly involved in setting Iq. This
junction temperature is not accessible to a thermal compensation system,
and measuring the heatsink temperature instead provides a poor approx-
imation,  attenuated  by  the  thermal  resistance  from  junction  to  heatsink
mass,  and  heavily  time-averaged  by  heatsink  thermal  inertia.  This  can
cause serious production problems in initial setting up; any drift of Iq will
be very slow as a lot of metal must warm up.

For EF outputs, the bias generator must attempt to establish an output bias
voltage that is a summation of four driver and output Vbe’s. These do not
vary in the same way. It seems at first a bit of a mystery how the EF stage,
which still seems to be the most popular output topology, works as well as
it  does.  The  probable  answer  is  Figure  12.1,  which  shows  how  driver
dissipation  (averaged  over  a  cycle)  varies  with  peak  output  level  for  the
three  kinds  of  EF  output  described  on  page  113,  and  for  the  CFP
configuration.  The  SPICE  simulations  used  to  generate  this  graph  used  a
triangle  waveform,  to  give  a  slightly  closer  approximation  to  the  peak-
average  ratio  of  real  waveforms.  The  rails  were  +/–50 V,  and  the  load
8 !.

It is clear that the driver dissipation for the EF types is relatively constant
with  power  output,  while  the  CFP  driver  dissipation,  although  generally
lower, varies strongly. This is a consequence of the different operation of
these two kinds of output. In general, the drivers of an EF output remain
conducting to some degree for most or all of a cycle, although the output
devices are certainly off half the time. In the CFP, however, the drivers turn
off almost in synchrony with the outputs, dissipating an amount of power
that varies much more with output. This implies that EF drivers will work at
roughly the same temperature, and can be neglected in arranging thermal
compensation; the temperature-dependent element is usually attached to
the  main  heatsink,  in  an  attempt  to  compensate  for  the  junction
temperature of the outputs alone. The Type I EF output keeps its drivers at
the most constant temperature; this may (or may not) have something to do
with why it is the most popular of the EF types.

(The above does not apply to integrated Darlington outputs, with drivers
and assorted emitter resistors combined in one ill-conceived package, as
the driver sections are directly heated by the output junctions. This would

334