ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 538
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
р1и не обнаруживает — с вероятностью 1 — р1 . Кроме того, иногда браковщик допускает ошибку, бракуя доброкачественное изделие; это происходит с вероятностью р2. За смену браковщик осматривает N изделий. Найти вероятность Rтого, что хотя бы одно из них будет квалифицировано им неправильно: то есть, будучи дефектным, отнесено к доброкачественным, или же наоборот (считается, что результаты осмотра отдельных изделий независимы).
Два баскетболиста поочередно бросают мяч в корзину до первого попадания. Вероятность попадания первого – 0,6, а второго – 0,3. Найти закон распределения числа бросков до первого попадания.
Дана функция распределения случайной величины Х

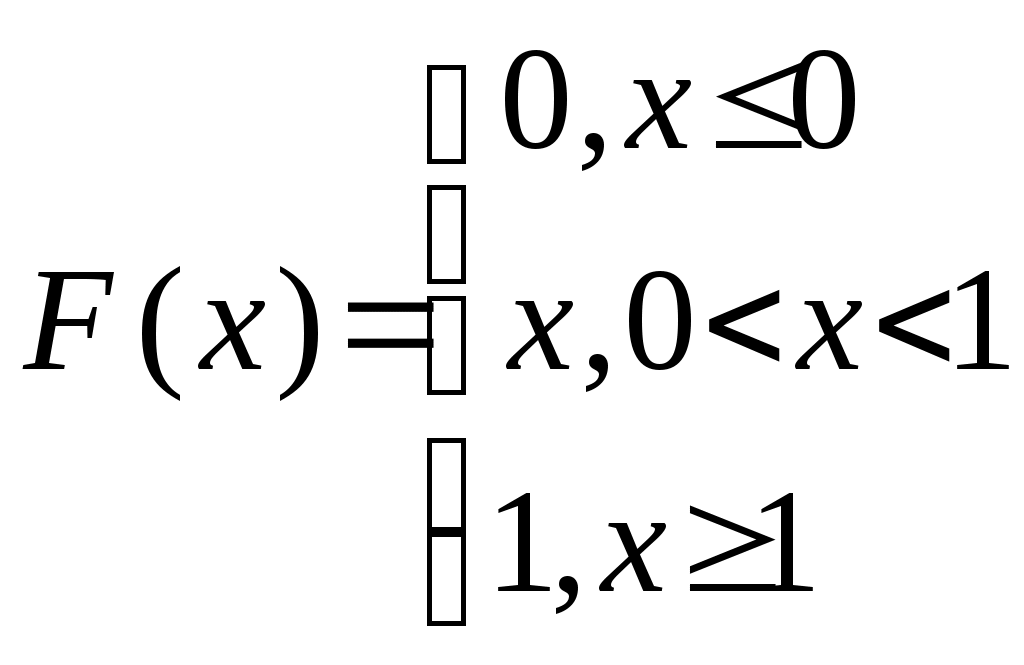 Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х два раза попадет в интервал (0,2;0,6).
Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х два раза попадет в интервал (0,2;0,6).
Диаметр втулки должен быть равен 7,5 мм. Ошибки изготовления нормальны с m=0 и =0,05 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Какова вероятность того, что втулка будет первого сорта?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 88
Какова вероятность, что все k раз извлекался один и тот же шар?
При этом изделий сразу бракуется и далее не проверяется. Найти вероятности событий:
А – изделие будет забраковано; В – изделие забракует третий контролер.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 89
р. Изделие осматривается одним контролером; он обнаруживает имеющийся дефект с Вероятностью р1 г а если дефект не обнаружен, пропускает изделие в готовую продукцию. Кроме того, контролер может по ошибке забраковать изделие, не имеющее дефекта; вероятность этого равна q1. Найти вероятности следующих событий:
А = {изделие забраковано};
В = {изделие забраковано, но по ошибке};
С = {изделие пропущено в готовую продукцию с дефектом}.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 90
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 91
Вероятность того, что двигатель начнет работать при втором включении зажигания;
Вероятность того, что для ввода двигателя в работу придется включить зажигание не более двух раз.

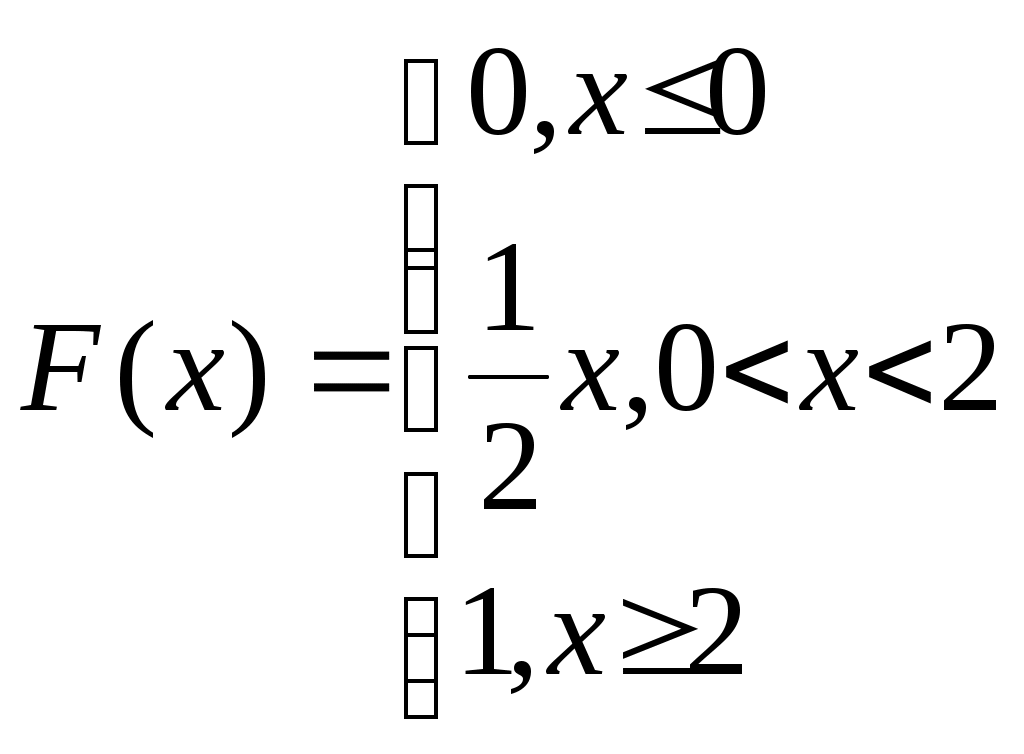 Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х три раза попадет в интервал (0,25;1).
Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х три раза попадет в интервал (0,25;1).
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.92.
Два баскетболиста поочередно бросают мяч в корзину до первого попадания. Вероятность попадания первого – 0,6, а второго – 0,3. Найти закон распределения числа бросков до первого попадания.
Дана функция распределения случайной величины Х
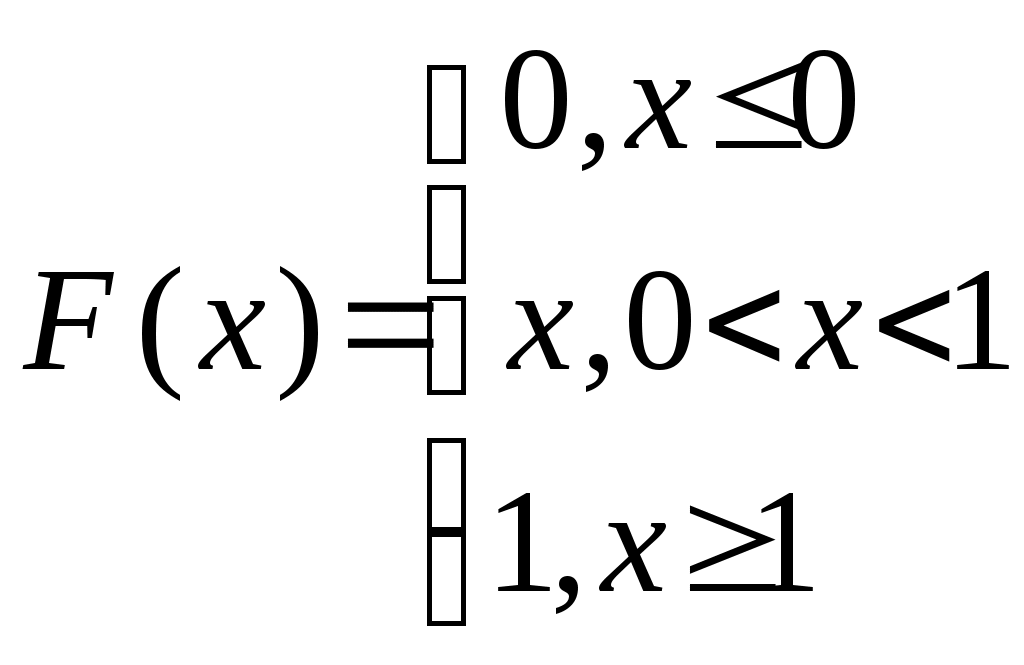 Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х два раза попадет в интервал (0,2;0,6).
Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х два раза попадет в интервал (0,2;0,6).Диаметр втулки должен быть равен 7,5 мм. Ошибки изготовления нормальны с m=0 и =0,05 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Какова вероятность того, что втулка будет первого сорта?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 88
-
Брошены две игральные кости. Какова вероятность того, что сумма выпавших очков не больше их произведения? Найти условную вероятность того, что выпали две пятерки, если известно, что сумма выпавших очков делится на пять?
-
Из урны, содержащей k шаров, извлекаем по одному, возвращаем и перемешиваем. Это повторяется k раз. Какова вероятность того, что все шары извлекались по одному разу?
Какова вероятность, что все k раз извлекался один и тот же шар?
-
Изделие может иметь дефект с вероятностью p. Его осматривают последовательно k контролеров. i – ый контролер обнаруживает дефект с вероятностью pi.
При этом изделий сразу бракуется и далее не проверяется. Найти вероятности событий:
А – изделие будет забраковано; В – изделие забракует третий контролер.
-
Батарея произвела 6 выстрелов по объекту. Вероятность попадания при одном выстреле равна 0,3. Найти наивероятнейшее число попаданий. Найти вероятность разрушения объекта, если для этого достаточно двух попаданий.
-
На сборку поступают детали от двух поставщиков в равных количествах. Брак первого поставщика составляет 5%, второго – 3%. Наугад берем две детали. Они оказались небракованными. Какова вероятность, что они от первого поставщика?
-
В коробке пять заготовок. Вероятность сделать годную деталь равна 0,8. Если испортили, то берут следующую заготовку. Найти закон распределения и числовые характеристики числа заготовок, оставшихся после наших попыток сделать одну деталь.
-
Автобусы идут с интервалом 5 минут. Предполагая, что время ожидания распределено равномерно в этом интервале, найти функцию распределения времени ожидания и вероятность того, что ждать придется менее двух минут.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 89
-
Случайная точка равномерно распределена внутри квадрата со стороной, равной а. Найти вероятность того, что расстояние от диагонали квадрата до точки больше а√2/8.
-
Бросаем две игральные кости. Какова вероятность того, что на одной из них больше очков? Какова вероятность того, что на первой больше очков?
-
Завод изготовляет изделия определенного типа; каждое изделие имеет дефект с вероятностью1 2 3 4 5 6 7 8
р. Изделие осматривается одним контролером; он обнаруживает имеющийся дефект с Вероятностью р1 г а если дефект не обнаружен, пропускает изделие в готовую продукцию. Кроме того, контролер может по ошибке забраковать изделие, не имеющее дефекта; вероятность этого равна q1. Найти вероятности следующих событий:
А = {изделие забраковано};
В = {изделие забраковано, но по ошибке};
С = {изделие пропущено в готовую продукцию с дефектом}.
-
В первой урне 5 белых, 11 черных и 8 красных шаров, а во второй 19 белых, 8 черных и 6 красных. Из каждой урны извлекают по одному шару. Какова вероятность того, что шары будут одного цвета? Какова вероятность появления разноцветных шаров в этом же эксперименте? Какова вероятность, что оба шара черные, если известно, что первый шар черный?
-
На пустую шахматную доску случайно ставится слон. Найти закон распределения числа «битых» клеток.
-
Ошибки прибора распределены нормально с нулевым мат.ожиданием и ско, равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза из пяти измерений?
-
Диаметр втулки должен быть равен 7,5 мм. Ошибки изготовления нормальны с m=0 и =0,05 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Какова вероятность того, что втулка будет первого сорта?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 90
-
На шахматную доску случайным образом ставят две ладьи. Какова вероятность того, что они не «бьют» друг друга? То же для случая двух слонов.
-
Партия из 100 деталей подвергается выборочному контролю. Для этого берут наугад 5 штук и, если среди них есть хотя бы одна дефектная, то бракуем всю партию. Какова вероятность этого события, если на самом деле в партии 5 дефектных деталей? Как изменится эта вероятность, если после проверки каждая деталь возвращается в партию и перемешивается?
-
Из колоды в 36 карт извлекаем две. Какова вероятность того, что это будут две дамы или две черные масти?
-
Три стрелка делают по пять независимых выстрелов по мишени. Вероятности попаданий при одном выстреле для этих стрелков таковы 0,7 , 0,8 , 0,9. Выигрывает тот, кто сделает больше всех попаданий. Найти вероятность ничьей.
-
Расследуются причины авиакатастрофы, о которых можно сделать 4 гипотезы: H1, H2, H3, H4. Согласно статистике P(H1)=0,2 , P(H2)=0,4 , P(H3)=0,3 , P(H4)=0,1. Вероятности воспламенения при выполнении гипотез равны соответственно 0,9 , 0 , 0,2 , 0,3. Известно, что воспламенения не было. Какая гипотеза вероятнее других?
-
Студент знает 6 вопросов из 10. Наугад вытягивает 3. Найти закон распределения и числовые характеристики с.в. Х – число известных вопросов среди взятых.
-
Интервал времени между отказами системы имеет функцию распределения вида F(t)=1-e-t, t>1. Определить плотность распределения и числовые характеристики. Найти вероятность того, что интервал между отказами превысит MT.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар. 91
-
В коробке 6 пронумерованных шаров. По одному извлекаем все. Какова вероятность того, что сначала выйдут все четные, а потом нечетные? номера появятся в возрастающем порядке?
-
При включении зажигания двигатель начинает работать с вероятностью р. Найти:
Вероятность того, что двигатель начнет работать при втором включении зажигания;
Вероятность того, что для ввода двигателя в работу придется включить зажигание не более двух раз.
-
Если монету подбрасывают семь раз, то какова вероятность выпадания четырех "решек"?
-
На вход радиолокационного устройства с вероятностью р поступает смесь полезного сигнала с помехой, а с вероятностью 1—р только одна помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие какого-то сигнала с вероятностью р1 ; если только помеха — с вероятностью р2. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе имеется полезный сигнал.
-
Производится стрельба по цели до первого попадания. На стрельбу отпущено 4 снаряда. Вероятность попадания при одном выстреле 0,3. Попадания независимы. Найти математическое ожидание числа израсходованных снарядов.
-
Дана функция распределения случайной величины Х
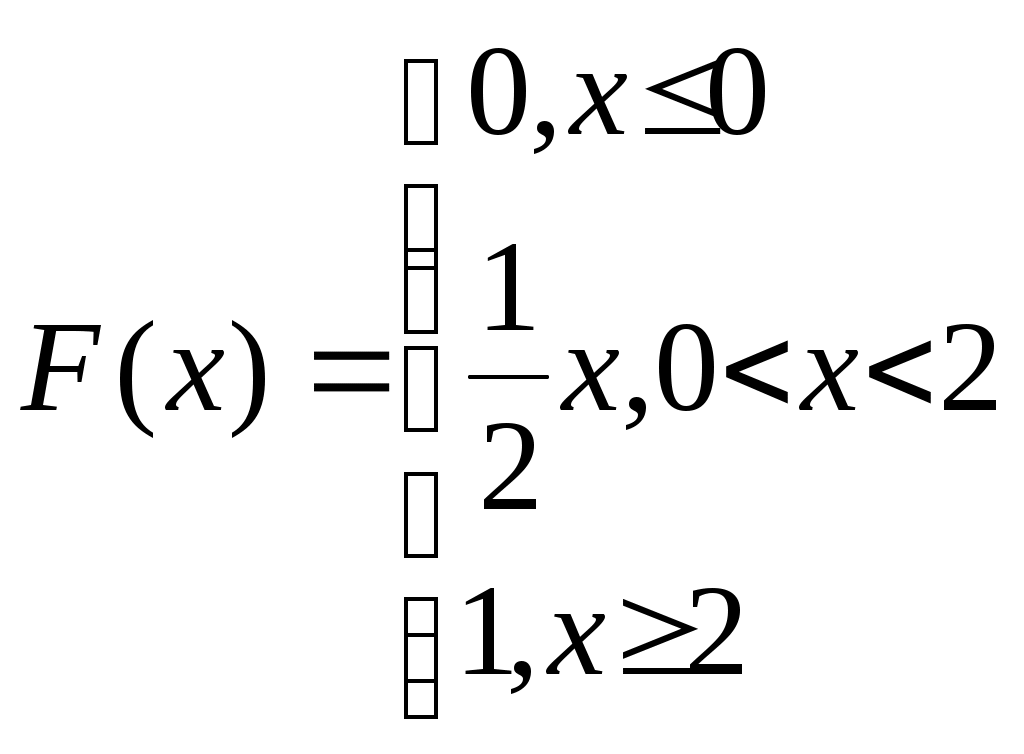 Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х три раза попадет в интервал (0,25;1).
Найти плотность распределения, числовые характеристики. Найти вероятность того, что в четырех независимых испытаниях с.в.Х три раза попадет в интервал (0,25;1).-
Отклонение размера детали от номинала подчинено нормальному закону с m=0 и σ=0,12мм. Если отклонение Δх < 0,02 , то деталь годится для изделия №1. Если не годится для изделия №1, но отклонение в пределах –0,1< Δх < 0,03, то для изделия №2 . Какова вероятность того, что деталь нельзя будет использовать? Какова вероятность того, что деталь подойдет только для изделия №2?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.92.
-
Известно, что три последние цифры номера телефона различны, но неизвестно какие. Мы набираем их наугад. Какова вероятность того, что придется звонить не менее трех раз?