Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx

Индивидуальный проект на тему: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.ПротоколДиффи-Хеллмана.Вместоключаклассическойкриптосистемыможновзятьслучайную точку(x,y),Рассмотрим пример. E – это эллиптическая кривая и P – это точка этойкривой. Абонент А выбираетслучайноечисло????, вычисляет координатыточки????????иотправляетабонентуВ.АбонентВделаеттожесамоеиотправляетабонентуА.Точка????=????????????являетсяобщимключом.АбонентА вычисляет эту точку, умножая свой ключ на ключ полученный от абонентаВ,аВвычисляет, умножаясвойключнаполученныйключабонентаA.Благодаря тому что группа точек является абелевой, Результат не зависит оттого в каком порядке буду происходить вычисления, тогда абоненты получатодинаковуюточку(x,y)имогутиспользоватькоординатуxкакключодинаковойкриптосистемы.Проблемойдлястороннихлюдейбудетввычислении секретной точки, так как они не будут знать секретные ключиабонентов.Вэтом изаключаетсяпроблема Диффи-Хеллмана.

1. Протокол Дифии-Хеллмана

Передача информации с помощью открытых каналов была большойпроблемой. Для этой проблемы нашлось решение после того как появилсяалгоритмДиффи-Хеллмана.Этоталгоритмдалвозможностьпересылатьсообщения без отправки каких-либо полезных сведений для расшифровки.Сам алгоритм позволяет пользователям обмениваться ключами без опасности

---

перехватаинформации.КриптографиюсоткрытымиключамипредложилииспользоватьУитфилдДиффи иМартин Хеллман.Онипривнесливкриптографиюпонятиечтоможноиспользоватьключишифрованияирасшифрования—исключаявозможностьутечкиинформации закрытого ключа с помощью открытого ключа. Впервые этоталгоритмбылпредставленнаНациональнойкомпьютернойконференции1976 года.Нижемыопишемего числовуюреализацию.

2. Числовая реализация

Возьмемвпримерпростуюситуацию.АбонентуАнужноотправитьсообщение абоненту В и злоумышленник пытается его перехватить.Логичнымрешениембудетшифрование,нодажееслиспособшифрованияизвестензлоумышленнику,тобезключаонегонерасшифрует.ОднакодлярасшифрованияабонентуАнеобходимключабонентаВ,которыйонпередастпосети,вэтовремязлоумышленникможетперехватитьегоирасшифровать сообщение. 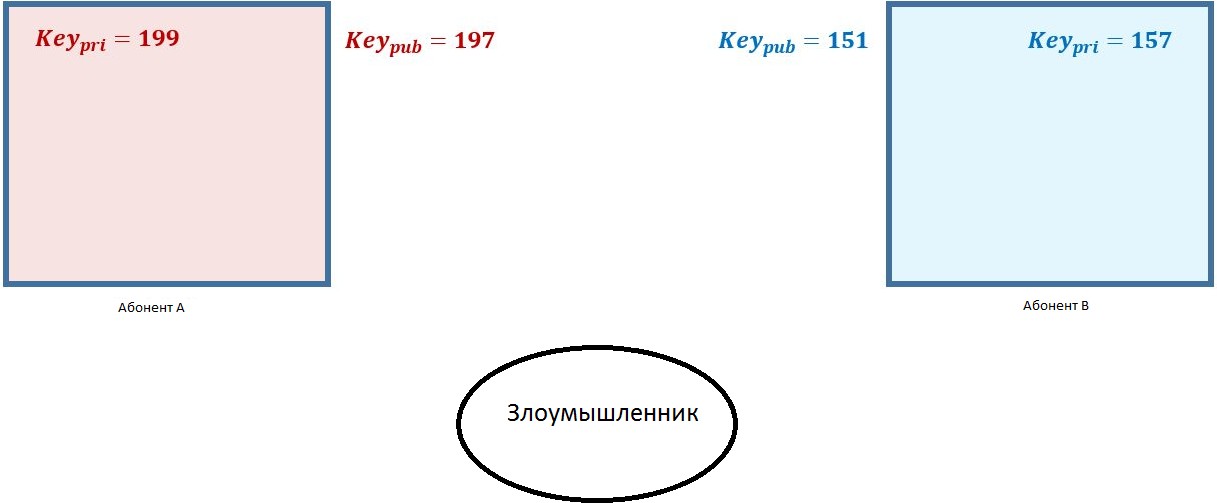Эту проблему решает протокол Диффи-Хеллмана.Диффи-Хеллманработаетпопринципунеполногообменаключомшифрованияпосети.Укаждойстороныестьоткрытыйключ(которыйможетвидетькаждый,включаязлоумышенника)изакрытыйключ(егоможетвидетьтолькопользователькомпьютера).Нарисунке3.1показанасхемаличных иоткрытых ключей.Рисунок3.1–СхемаключейиабонентовПредположим,чтоабонентАнезнаетничегокромеоткрытогоключа

---

абонента В. Нужно создать частичный ключ шифрования используя 3 известных параметра. Открытый и закрытый ключ абонента А и открытый ключ абонента В.

Полученные полные ключи должны совпасть по значению. Заключается это вследующемсоотношении:(????^????????????????????)^????????????????????=(????^????????????????????)^????????????????????=????^???????????????????????? (3.5)В нем a и b это закрытые ключи, а g и p открытые ключи. Абонентам удалосьобменяться друг с другом по сети достаточным количеством информации,чтобысгенерировать общий ключ шифрования

---

, не ставя под угрозу свои закрытые ключи. После этого абонент В передает зашифрованное сообщение и абонент А расшифровывает его.

3.   1   2   3   4   5   6   7   8   9   ...   14

---

Программная реализация

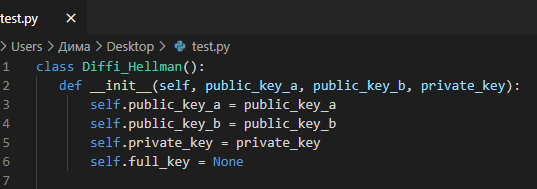
Перейдемкпрограммнойреализацииалгоритма.АлгоритмДиффи-Хеллмана реализован на языке Python, в среде разработки VSC (Visual StudioCode).Дляначаланамнужносоздатьконструктор.Дляэтогоиспользуемметодinit().Рисунок3.2–конструктордлясозданияключейВ этом конструкторе создаются переменные для открытых и закрытыхключей. 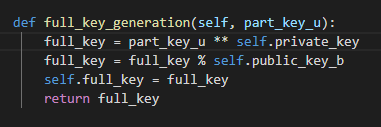Так как пользователь А будет знать лишь свой открытый, закрытыйключиоткрытыйключпользователяВ,намненужносоздаватьдополнительнуюпеременнуюдлязакрытогоключа.Вэтотметодмыпередаем два открытых ключа и закрытый ключ для каждого пользователя.Такжеимеетсяпеременнаядляполногоключа,которуювдальнейшеммыбудемвычислятьспомощьюоткрытыхичастичныхключей,поэтомунаданномэтапе она остается пустой.Далее нам нужна функция для генерации частичного ключа для обоихпользователей.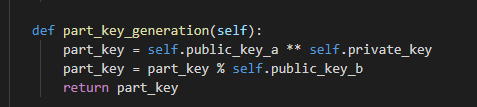Рисунок3.3–функциягенерациичастичногоключаВ этой функции мы вычисляем частичный ключ с помощью открытого,закрытогоключаодногопользователяиоткрытогоключадругогопользователя.Для вычисленияиспользуем формулы 3.1,3.2.Затем создаем функции для вычисления полного ключа. Для этого мыиспользуемнашичастичныеключи

---