Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 285
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
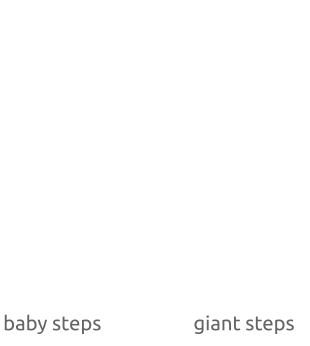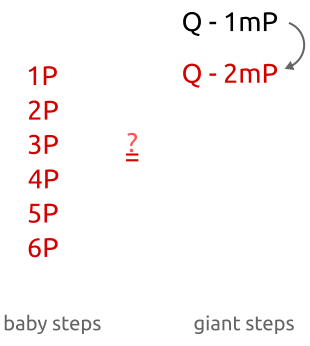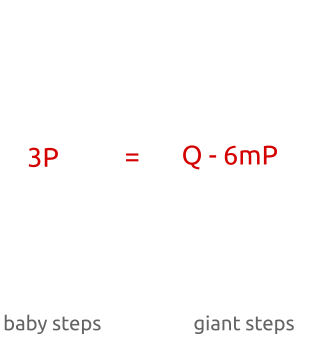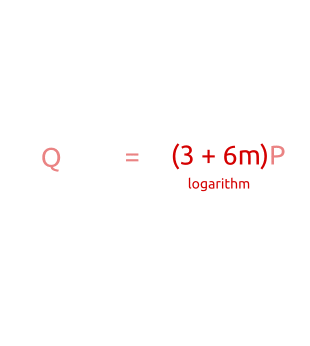
Алгоритм baby-step, giant-step: сначала мы вычисляем несколько точек с небольшим шагом и сохраняем их в хеш-таблице. Затем делаем великанские шаги и сравниваем новые точки с точками в хеш-таблице. Найдя соответствие, мы можем вычислить дискретный алгоритм простой перестановкой членов.
Чтобы понять, как работает алгоритм, забудем на минуту о том, что
кешируются, и возьмём уравнение . Рассмотрим, что из этого следует:-
При мы проверяем, равно ли числу , где — одно из целых от 0 до . Таким образом, мы сравниваем со всеми точками от до . -
При мы проверяем равно ли числу . Мы сравниваем со всеми точками от до . -
При мы сравниваем со всеми точками от до . -
... -
При мы сравниваем со всеми точками от до .
В итоге мы проверили все точки от
до
(то есть все возможные точки), выполнив не более
сложений и умножений (ровно для «детских шагов», не более для «великанских шагов»).Если считать, что поиск в хеш-таблице занимает время
то легко увидеть, что этот алгоритм имеет временную и пространственную сложность (или , если учесть битовую длину). Это всё ещё экспоненциальное время, но оно намного лучше, чем при атаке перебором.Baby-step giant-step на практике
Имеет смысл разобраться, что же значит сложность
на практике. Возьмём стандартизированную кривую: prime192v1 (она же secp192r1, ansiX9p192r1). Эта кривая имеет порядок = 0xffffffff ffffffff ffffffff 99def836 146bc9b1 b4d22831. Квадратный корень из — это примерно 7,922816251426434 · 1028 (почти восемьдесят октиллионов [прим. пер.: по короткой шкале]).Представим, что мы храним
точек в хеш-таблице. Предположим, что каждая точка занимает ровно 32 байта: для хеш-таблицы потребуется примерно 2,5 · 1030 байт памяти. Поискав в Интернете, можно узнать, что современная общая ёмкость накопителей всего мира имеет порядок зеттабайта (1021 байт). Это почти на десять порядков меньше, чем объём памяти, необходимый нашей хеш-таблице! Даже если бы точки занимали по 1 байт каждая, мы всё равно не смогли бы хранить их все.Это впечатляет, и впечатляет ещё сильнее, если вспомнить, что prime192v1 — это одна из кривых с наименьшим порядком. Порядок secp521r1 (ещё одной стандартной кривой NIST) равен примерно 6,9 · 10
156!
Эксперименты с baby-step giant-step
Я написал скрипт на Python, вычисляющий дискретные логарифмы с помощью алгоритма baby-step giant-step. Очевидно, что он работает только с кривыми малого порядка: не пытайтесь использовать secp521r1, если только не хотите получить MemoryError.
Скрипт выдаёт примерно такие выходные данные:
Curve: y^2 = (x^3 + 1x - 1) mod 10177
Curve order: 10331
p = (0x1, 0x1)
q = (0x1a28, 0x8fb)
325 * p = q
log(p, q) = 325
Took 105 steps
ρ Полларда
ρ Полларда — это ещё один алгоритм вычисления дискретных логарифмов. Он имеет ту же асимптотическую временную сложность
, что и baby-step giant-step, но его пространственная сложность равна всего . Если baby-step giant-step не мог решить дискретные логарифмы из-за огромных требований к памяти, может быть, ρ Полларда справится? Давайте проверим…Для начала ещё раз напомню задачу дискретного логарифмирования: найти для заданных
и целое , такое, что . В ρ-алгоритме Полларда мы будем решать немного другую задачу: найти для заданных и целые , , и , такие, что .Найдя четыре целых числа, мы сможем использовать уравнение
для вычисления : Теперь мы можем избавиться от
. Но прежде чем сделать это, вспомним, что наша подгруппа циклическая и имеет порядок , то есть коэффициенты, используемые при умножении точек, берутся по модулю : Принцип работы ρ Полларда прост: мы определяем псевдослучайную последовательность пар
. Эту последовательность пар можно использовать для генерирования последовательности точек . Поскольку и являются элементами одной циклической подгруппы,
последовательность точек
тоже циклическая.Это значит, что если мы обойдём нашу псевдослучайную последовательность пар
, то рано или поздно обнаружим цикл. То есть: мы найдём пару и другую отдельную пару , такие, что . Те же точки, отдельные пары: мы сможем применить приведённое выше уравнение для нахождения логарифма.Задача заключается в следующем: как обнаружить цикл эффективным способом?
Черепаха и заяц
Для обнаружения цикла мы можем проверить все возможные значения
и с помощью функции пересчёта пар, но при условии, что существует таких пар, алгоритм будет иметь сложность , что намного хуже атаки простым перебором.Но существует и более быстрый способ: алгоритм черепахи и зайца (также известный как алгоритм нахождения цикла Флойда). На рисунке ниже показан принцип работы метода черепахи и зайца, на котором основан ρ-алгоритм Полларда.
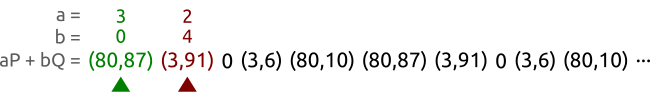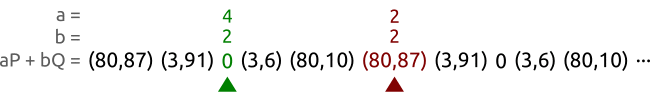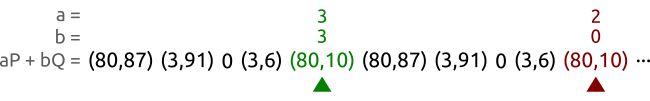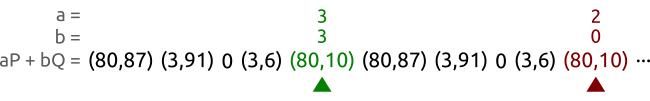
У нас есть кривая
и точки и . Точки принадлежат циклической подгруппе с порядком 5. Мы обходим последовательность пар с разными скоростями, пока не находим две разные пары и , дающих одну точку. В этом случае мы нашли пары и , что позволяет нам вычислить логарифм как . И на самом деле, у нас получилось .