Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx

Рисунок 3.4 – функция генерации полного ключа

В эту функцию мы передаем переменную part_key_u, это переменная, в которую мы передаем значение частичного ключа для каждого пользователя. Для пользователя А это частичный ключ В, а для пользователя В это частичный ключ А. Для вычисления используем формулы 3.3, 3.4.

Теперь создаем функции для шифрования и расшифровывания сообщения.



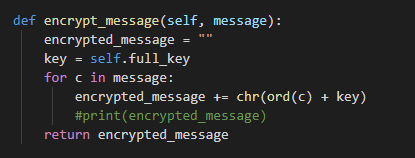
Рисунок 3.5 – функция шифрования сообщения

В этой функции каждый символ считывается и преобразовывается в целое число, после чего к этому значению прибавляется значение полного ключа и это число снова преобразуется снова в символ. Это происходит для каждого символа в нашем сообщении. Функция chr используется для преобразования значения integer в значение character. Функция ord() это функция обратная функции chr, она преобразует значение character в значение integer.

Далее создаем функцию для расшифровки сообщения. В нем мы так же используем функции chr и ord() для преобразования сообщения в числовое значение и обратно в словесное значение.



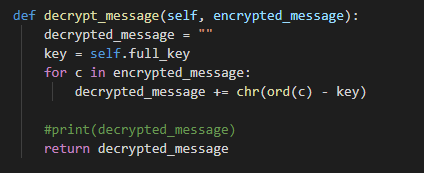
Рисунок 3.6 – функция расшифровки сообщения

Так как в функции зашифровывания сообщения мы прибавляли значение ключа к значению сообщения, то в этой функции мы наоборот вычитаем это значение из значения сообщения.

Переходим к части ввода информации.



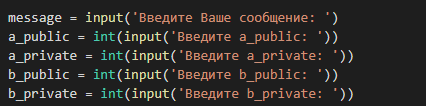
Рисунок 3.7 – ввод информации

Здесь мы задаем сообщение, которое мы хотим передать, вводим открытый ключ пользователя a, закрытый ключ пользователя a, открытый

---

ключ пользователя b и закрытый ключ пользователя b.



Рисунок 3.8 – вызов функции для передачи ключей

Здесь мы вызываем функцию Diffi_Hellman() и передаем туда значения ключей. Так как пользователям известны лишь 3 ключа (свой открытый, открытый собеседника и свой закрытый) мы передаем 3 значения.

Далее вычисляем частичные ключи для пользователя a и пользователя

b.




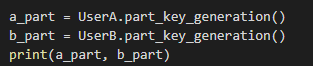
Рисунок 3.9 – вычисление частичных ключей

Для пользователя a вызываем функцию вычисления частичного ключа, тоже самое делаем и для пользователя b. И выводим их на экран.

Следующим шагом вычисляем полные ключи, для вычисления которых нам требуются частичные.



Рисунок 3.10 – вычисление полных ключей

Для пользователя a вызываем функцию вычисления полного ключа, тоже самое делаем и для пользователя b. При вызове этих функций мы передаем в них значение частичных ключей пользователей. И выводим их на экран.

Последним шагом будет зашифровывание сообщения, его расшифровка и вывод обоих сообщений на экран.



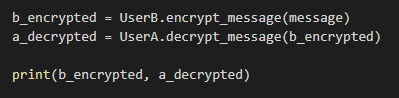
Рисунок 3.11 – шифрование и дешифрование сообщения

Здесь пользователь b вызывает функцию зашифровки сообщения и передает туда сообщение, введенное пользователем. Пользователь a вызывает функцию дешифровки сообщения и передает в нее зашифрованное

---

сообщение пользователя b. После всех вычислений мы выводим зашифрованное и расшифрованное сообщение.

4. 1   2   3   4   5   6   7   8   9   ...   14

---

Результаты

В качестве входных данных возьмем значения ключей из примера числовой реализации. В ней открытый ключ пользователя a 197, его закрытый ключ 199. У пользователя b открытый ключ 151, закрытый 157. В качестве сообщения возьмем «Hello, how u doing». Ниже на рисунке 3.12 продемонстрирован результат работы программы с такими входными данными.



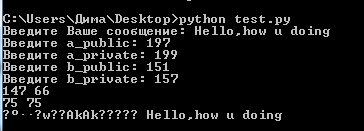
Рисунок 3.12 – результат работы программы

Как видно на рисунке результаты получились такие же, как и в числовой реализации. Открытый ключ пользователя a равен 147, а у b 66. Закрытый же ключ у них одинаков и равен 75 и в самом низу показано зашифрованное сообщение и расшифрованное.

Для исследования проверим как будет работать алгоритм если задать достаточно большое число в качестве ключей или такое число, при котором остаток от деления будет равен нулю.

Для начала проверим работу алгоритма при задании такого ключа при котором остаток от деления будет равен нулю.



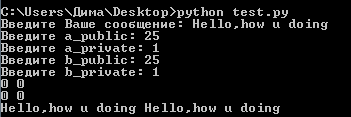
Рисунок 3.13 – получение нулевых ключей

Как видно на рисунке 3.13 если остаток от деления равен нулю, то частичные и полные ключи будут равны нулю, при этом сообщение не будет зашифровано. Т.е. пользователям нельзя задавать значения, при которых остаток от деления будет равен нулю.

Далее проверим работу алгоритма при больших значениях ключей.




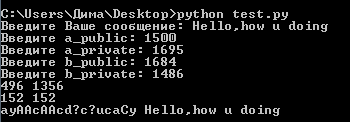
Рисунок 3.14 – работа алгоритма при больших значениях ключей Даже не

---

смотря на большие размеры ключей алгоритм работает

исправно без ошибок. Однако существует проблема вычислений таких больших значений при высчитывании ключей человеком, а не компьютером. Связано это с возведением в степень числа при котором получается слишком большое значение, из-за которого любой калькулятор будет давать ответ ∞ (бесконечность).

Тем, кто знаком с криптографией с открытым ключом, наверно известны аббревиатуры ECC, ECDH и ECDSA. Первая — это сокращение от Elliptic Curve Cryptography (криптография на эллиптических кривых), остальные — это названия основанных на ней алгоритмов.

Сегодня криптосистемы на эллиптических кривых используются в TLS, PGP и SSH, важнейших технологиях, на которых базируются современный веб и мир ИТ. Я уже не говорю о Bitcoin и других криптовалютах.

До того, как ECC стала популярной, почти все алгоритмы с открытым ключом основывались на RSA, DSA и DH, альтернативных криптосистемах на основе модулярной арифметики. RSA и компания по-прежнему популярны, и часто используются вместе с ECC. Однако несмотря на то, что магия, лежащая в фундаменте RSA и подобных ей алгоритмов легко объяснима и понятна многим, а грубые реализации пишутся довольно просто, основы ECC всё ещё являются для большинства людей загадкой.

В этой серии статей я познакомлю вас с основами мира криптографии на эллиптических кривых. Моя цель — не создание полного и подробного руководства по ECC (в Интернете полно информации по этой теме), а простой обзор ECC и объяснение того, почему её считают безопасной. Я не буду тратить время на долгие математические доказательства или скучные подробности реализации. Также я представлю полезные примеры с визуальными интерактивными инструментами и скриптами

---