Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 279
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
.
В частности, я рассмотрю следующие темы:
Для понимания статьи вам нужно знать основы теории множеств, геометрии и модулярной арифметики, понимать принципы симметричной и асимметричной криптографии. Наконец, вы должны чётко понимать, что такое «простая» и «сложная» задачи и их роли в криптографии.
Готовы? Приступим!
Во-первых: что такое эллиптическая кривая? В Wolfram MathWorld есть отличное и исчерпывающее определение. Но для нас достаточно того, что эллиптическая кривая — это просто множество точек, описываемое уравнением:

где , (это необходимо, чтобы исключить особые кривые). Приведённое выше уравнение называется обычной формулировкой Вейерштрасса для эллиптических кривых.
, (это необходимо, чтобы исключить особые кривые). Приведённое выше уравнение называется обычной формулировкой Вейерштрасса для эллиптических кривых.

Различные формы эллиптических кривых ( ,
,  изменяется от 2 до -3).
изменяется от 2 до -3).
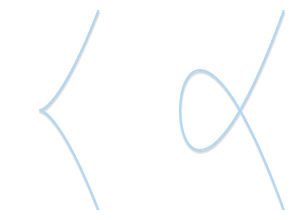
Виды особенностей: слева — кривая с точкой возврата (каспом) ( ). Справа — кривая с самопересечением (
). Справа — кривая с самопересечением ( ). Оба этих примера не являются полноценными эллиптическими кривыми.
). Оба этих примера не являются полноценными эллиптическими кривыми.
В зависимости от значений и
и  эллиптические кривые могут принимать на плоскости разные формы. Как можно легко увидеть и проверить, эллиптические кривые симметричны относительно оси
эллиптические кривые могут принимать на плоскости разные формы. Как можно легко увидеть и проверить, эллиптические кривые симметричны относительно оси  .
.
Для наших целей нам также понадобится, чтобы частью кривой являлась бесконечно удалённая точка (также известная как идеальная точка). С этого момента мы будем обозначать бесконечно удалённую точку символом 0 (ноль).
Если нам требуется явным образом учитывать точку в бесконечности, то определение эллиптической кривой можно уточнить следующим образом:

В математике группа — это множество, для которого мы определили двоичную операцию, называемую «сложением» и обозначаемую символом +. Чтобы множество было группой, сложение нужно определить таким образом, чтобы оно соответствовало четырём следующим свойствам:
было группой, сложение нужно определить таким образом, чтобы оно соответствовало четырём следующим свойствам:
Если мы добавим пятое требование:
то группа называется абелевой группой.
При обычной записи сложения множество целых чисел является группой (более того, это абелева группа). Множество натуральных чисел
является группой (более того, это абелева группа). Множество натуральных чисел  , однако, не является группой, потому что не удовлетворяет четвёртому свойству.
, однако, не является группой, потому что не удовлетворяет четвёртому свойству.
Группы удобны тем, что если мы докажем соблюдение всех четырёх свойств, то получим автоматически некоторые другие свойства «в нагрузку». Например:
единичный элемент уникален; кроме того, обратные величины уникальны, то есть: для каждого существует единственное
существует единственное  , такое, что
, такое, что  (и мы можем записать
(и мы можем записать  как
как  ). Непосредственно или косвенно эти и другие свойства групп очень пригодятся нам в будущем.
). Непосредственно или косвенно эти и другие свойства групп очень пригодятся нам в будущем.
Мы можем определить группу для эллиптических кривых. А именно:

Сумма трёх точек, находящихся на одной прямой, равна 0.
Стоит учесть, что в последнем правиле нам требуются только три точки на одной прямой, и порядок расположения этих трёх точек не важен. Это значит, что если три точки ,
,  и
и  лежат на одной прямой, то
лежат на одной прямой, то  . Таким образом мы интуитивно доказали, что наш оператор + обладает свойствами ассоциативности и коммутативности: мы находимся в абелевой группе.
. Таким образом мы интуитивно доказали, что наш оператор + обладает свойствами ассоциативности и коммутативности: мы находимся в абелевой группе.
Пока всё идёт отлично. Но как нам вычислить сумму двух произвольных точек?
Благодаря тому, что мы находимся в абелевой группе, то можем записать как
как  . Это уравнение в такой форме позволяет нам вывести геометрический способ вычисления суммы двух точек
. Это уравнение в такой форме позволяет нам вывести геометрический способ вычисления суммы двух точек  и
и  :
:
В частности, я рассмотрю следующие темы:
-
Эллиптические кривые над вещественными числами и групповой закон -
Эллиптические кривые над конечными полями и задача дискретного логарифмирования -
Генерирование пар ключей и два алгоритма ECC: ECDH и ECDSA -
Алгоритмы для взлома защиты ECC и сравнение с RSA
Для понимания статьи вам нужно знать основы теории множеств, геометрии и модулярной арифметики, понимать принципы симметричной и асимметричной криптографии. Наконец, вы должны чётко понимать, что такое «простая» и «сложная» задачи и их роли в криптографии.
Готовы? Приступим!
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Эллиптические кривые
Во-первых: что такое эллиптическая кривая? В Wolfram MathWorld есть отличное и исчерпывающее определение. Но для нас достаточно того, что эллиптическая кривая — это просто множество точек, описываемое уравнением:

где
 , (это необходимо, чтобы исключить особые кривые). Приведённое выше уравнение называется обычной формулировкой Вейерштрасса для эллиптических кривых.
, (это необходимо, чтобы исключить особые кривые). Приведённое выше уравнение называется обычной формулировкой Вейерштрасса для эллиптических кривых.
Различные формы эллиптических кривых (
 ,
,  изменяется от 2 до -3).
изменяется от 2 до -3).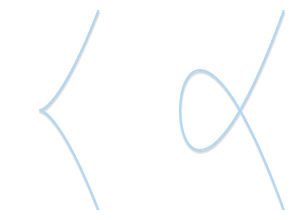
Виды особенностей: слева — кривая с точкой возврата (каспом) (
 ). Справа — кривая с самопересечением (
). Справа — кривая с самопересечением ( ). Оба этих примера не являются полноценными эллиптическими кривыми.
). Оба этих примера не являются полноценными эллиптическими кривыми.В зависимости от значений
 и
и  эллиптические кривые могут принимать на плоскости разные формы. Как можно легко увидеть и проверить, эллиптические кривые симметричны относительно оси
эллиптические кривые могут принимать на плоскости разные формы. Как можно легко увидеть и проверить, эллиптические кривые симметричны относительно оси  .
.Для наших целей нам также понадобится, чтобы частью кривой являлась бесконечно удалённая точка (также известная как идеальная точка). С этого момента мы будем обозначать бесконечно удалённую точку символом 0 (ноль).
Если нам требуется явным образом учитывать точку в бесконечности, то определение эллиптической кривой можно уточнить следующим образом:

Группы
В математике группа — это множество, для которого мы определили двоичную операцию, называемую «сложением» и обозначаемую символом +. Чтобы множество
 было группой, сложение нужно определить таким образом, чтобы оно соответствовало четырём следующим свойствам:
было группой, сложение нужно определить таким образом, чтобы оно соответствовало четырём следующим свойствам:-
замыкание: если и
и  входят в
входят в  , то
, то  входит в
входит в  ;
; -
ассоциативность: ;
; -
существует единичный элемент 0, такой, что ;
; -
у каждого элемента есть обратная величина, то есть: для каждого существует такое
существует такое  , что
, что  .
.
Если мы добавим пятое требование:
-
коммутативность: ,
,
то группа называется абелевой группой.
При обычной записи сложения множество целых чисел
 является группой (более того, это абелева группа). Множество натуральных чисел
является группой (более того, это абелева группа). Множество натуральных чисел  , однако, не является группой, потому что не удовлетворяет четвёртому свойству.
, однако, не является группой, потому что не удовлетворяет четвёртому свойству.Группы удобны тем, что если мы докажем соблюдение всех четырёх свойств, то получим автоматически некоторые другие свойства «в нагрузку». Например:
единичный элемент уникален; кроме того, обратные величины уникальны, то есть: для каждого
 существует единственное
существует единственное  , такое, что
, такое, что  (и мы можем записать
(и мы можем записать  как
как  ). Непосредственно или косвенно эти и другие свойства групп очень пригодятся нам в будущем.
). Непосредственно или косвенно эти и другие свойства групп очень пригодятся нам в будущем.Групповой закон для эллиптических кривых
Мы можем определить группу для эллиптических кривых. А именно:
-
элементы группы являются точками эллиптической кривой; -
единичный элемент — это бесконечно удалённая точка 0; -
обратная величина точки — это точка, симметричная относительно оси
— это точка, симметричная относительно оси  ;
; -
сложение задаётся следующим правилом: сумма трёх ненулевых точек ,
,  и
и  , лежащих на одной прямой, будет равна
, лежащих на одной прямой, будет равна  .
.

Сумма трёх точек, находящихся на одной прямой, равна 0.
Стоит учесть, что в последнем правиле нам требуются только три точки на одной прямой, и порядок расположения этих трёх точек не важен. Это значит, что если три точки
 ,
,  и
и  лежат на одной прямой, то
лежат на одной прямой, то  . Таким образом мы интуитивно доказали, что наш оператор + обладает свойствами ассоциативности и коммутативности: мы находимся в абелевой группе.
. Таким образом мы интуитивно доказали, что наш оператор + обладает свойствами ассоциативности и коммутативности: мы находимся в абелевой группе.Пока всё идёт отлично. Но как нам вычислить сумму двух произвольных точек?
Геометрическое сложение
Благодаря тому, что мы находимся в абелевой группе, то можем записать
 как
как  . Это уравнение в такой форме позволяет нам вывести геометрический способ вычисления суммы двух точек
. Это уравнение в такой форме позволяет нам вывести геометрический способ вычисления суммы двух точек  и
и  :
: