Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 277
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
если мы проведём линию, проходящую через 
и , эта прямая пересечёт третью точку кривой (это подразумевается, потому что , и находятся на одной прямой). Если мы возьмём обратную величину этой точки , мы найдём сумму .
Проводим прямую через и . Прямая пересекает третью точку . Симметричная ей точка является результатом .
Геометрический способ работает, но требует усовершенствования. В частности, нам нужно ответить на несколько вопросов:
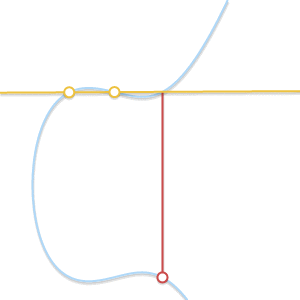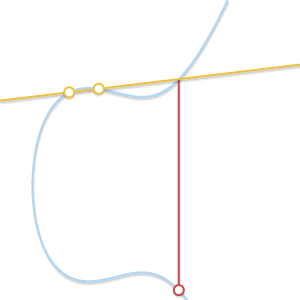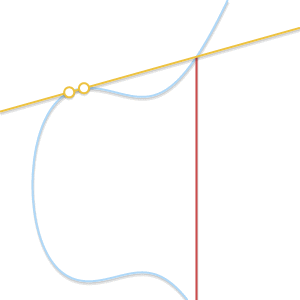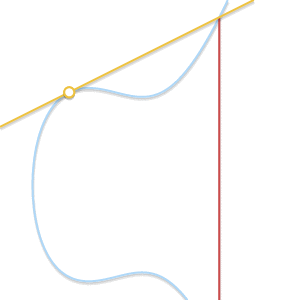
При сближении двух точек проходящая через них прямая становится касательной к кривой.
Поскольку стремится к , прямая, проходящая через и становится касательной к кривой. В свете этого мы можем сказать, что , где — это точка пересечения между кривой и касательной к кривой в точке .
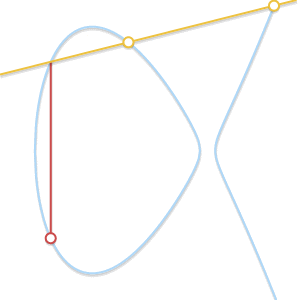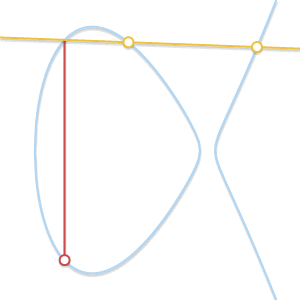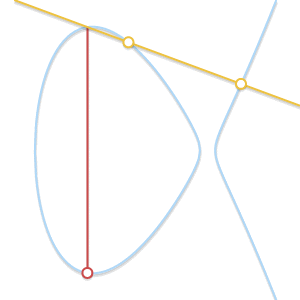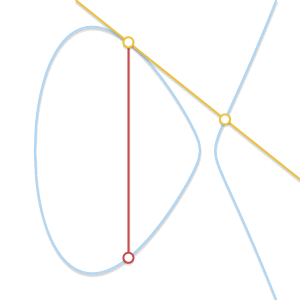
Если наша прямая пересекает только две точки, то это значит, что она является касательной к кривой. Легко увидеть, как результат сложения становится симметричным одной из двух точек.
Предположим, что является точкой касания. В предыдущем случае мы записали . Это уравнение теперь превращается в . С другой стороны, если бы точкой касания была , то правильным было бы уравнение .
Геометрический способ теперь полон и учитывает все случаи. С помощью карандаша и линейки мы можем выполнить сложение всех точек любой эллиптической кривой. Если хотите попробовать, взгляните на визуальный инструмент на HTML5/JavaScript, созданный мной для вычисления сумм эллиптических кривых
.
Если мы хотим, чтобы сложением точек занимался компьютер, нужно превратить геометрический способ в алгебраический. Преобразование вышеизложенных правил в набор уравнений может казаться простым, но на самом деле оно довольно утомительно, потому что требует решения кубических уравнений. Поэтому я изложу только результаты.
Для начала давайте избавимся от самых раздражающих тупиковых ситуаций. Мы уже знаем, что , и знаем, что . Поэтому в наших уравнениях мы будем избегать этих двух случаев и рассмотрим только две ненулевые несимметричные точки и .
Если и не совпадают ( ), то проходящая через них прямая имеет наклон:
Пересечение этой прямой с эллиптической кривой — это третья точка :
или, аналогично:
Поэтому (обратите внимание на знаки и помните, что ).
Если бы нам нужно было проверить правильность результата, то пришлось бы проверить, принадлежит ли кривой и находятся ли , и на одной прямой. Проверка нахождения на одной прямой тривиальна, а проверка принадлежности кривой — нет, потому что нам придётся решать кубическое уравнение, что совсем невесело.
Вместо этого давайте поэкспериментируем с примером: согласно визуальному инструменту, при и , принадлежащих кривой , их сумма равна . Давайте проверим, соответствует ли это уравнениям:
Да, всё верно!
Заметьте, что эти уравнения работают даже в случае, когда точка или является точкой касания. Давайте проверим на и .
Мы получили результат , который совпадает с результатом, полученным в визуальном инструменте.
К случаю нужно относиться немного иначе: уравнения для и остаются теми же, но с учётом того, что нам придётся использовать для наклона другое уравнение:
Заметьте, что, как можно ожидать, это выражение для является первой производной:
Чтобы доказать правильность этого результата, достаточно убедиться, что принадлежит к кривой и что прямая, проходящая через и , имеет только два пересечения с кривой. Но мы снова не будем доказывать это и вместо этого разберём пример: .
и , эта прямая пересечёт третью точку кривой (это подразумевается, потому что , и находятся на одной прямой). Если мы возьмём обратную величину этой точки , мы найдём сумму . Проводим прямую через
и . Прямая пересекает третью точку . Симметричная ей точка является результатом .Геометрический способ работает, но требует усовершенствования. В частности, нам нужно ответить на несколько вопросов:
-
Что если или ? Разумеется, мы не сможем провести прямую (0 не находится на плоскости ). Но поскольку мы определили 0 как единичный элемент, и для любой и любой . -
Что если ? В этом случае прямая, проходящая через две точки, вертикальна, и не пересекает третью точку. Но если является обратной величиной , то из определения обратной величины. -
Что если ? В этом случае через точку проходит бесконечное количество прямых. Здесь всё становится немного сложнее. Но представим, что точка . Что произойдёт, если мы заставим стремиться к , всё больше приближаясь к ней?
При сближении двух точек проходящая через них прямая становится касательной к кривой.
Поскольку
стремится к , прямая, проходящая через и становится касательной к кривой. В свете этого мы можем сказать, что , где — это точка пересечения между кривой и касательной к кривой в точке .-
Что если , но третьей точки нет? В этом случае ситуация похожа на предыдущую. На самом деле, в этой ситуации прямая, проходящая через и , является касательной к кривой.
Если наша прямая пересекает только две точки, то это значит, что она является касательной к кривой. Легко увидеть, как результат сложения становится симметричным одной из двух точек.
Предположим, что
является точкой касания. В предыдущем случае мы записали . Это уравнение теперь превращается в . С другой стороны, если бы точкой касания была , то правильным было бы уравнение .Геометрический способ теперь полон и учитывает все случаи. С помощью карандаша и линейки мы можем выполнить сложение всех точек любой эллиптической кривой. Если хотите попробовать, взгляните на визуальный инструмент на HTML5/JavaScript, созданный мной для вычисления сумм эллиптических кривых
.
Алгебраическое сложение
Если мы хотим, чтобы сложением точек занимался компьютер, нужно превратить геометрический способ в алгебраический. Преобразование вышеизложенных правил в набор уравнений может казаться простым, но на самом деле оно довольно утомительно, потому что требует решения кубических уравнений. Поэтому я изложу только результаты.
Для начала давайте избавимся от самых раздражающих тупиковых ситуаций. Мы уже знаем, что
, и знаем, что . Поэтому в наших уравнениях мы будем избегать этих двух случаев и рассмотрим только две ненулевые несимметричные точки и .Если
и не совпадают ( ), то проходящая через них прямая имеет наклон: Пересечение этой прямой с эллиптической кривой — это третья точка
: или, аналогично:
Поэтому
(обратите внимание на знаки и помните, что ).Если бы нам нужно было проверить правильность результата, то пришлось бы проверить, принадлежит ли
кривой и находятся ли , и на одной прямой. Проверка нахождения на одной прямой тривиальна, а проверка принадлежности кривой — нет, потому что нам придётся решать кубическое уравнение, что совсем невесело.
Вместо этого давайте поэкспериментируем с примером: согласно визуальному инструменту, при
и , принадлежащих кривой , их сумма равна . Давайте проверим, соответствует ли это уравнениям: Да, всё верно!
Заметьте, что эти уравнения работают даже в случае, когда точка
или является точкой касания. Давайте проверим на и . Мы получили результат
, который совпадает с результатом, полученным в визуальном инструменте.К случаю
нужно относиться немного иначе: уравнения для и остаются теми же, но с учётом того, что нам придётся использовать для наклона другое уравнение: Заметьте, что, как можно ожидать, это выражение для
является первой производной: Чтобы доказать правильность этого результата, достаточно убедиться, что
принадлежит к кривой и что прямая, проходящая через и , имеет только два пересечения с кривой. Но мы снова не будем доказывать это и вместо этого разберём пример: .