Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 284
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
-
Сложение:
-
Вычитание: -
Умножение: -
Аддитивная инверсия: . Действительно: -
Мультипликативная инверсия:
Если эти уравнения вам незнакомы и вы хотите изучить основы модулярной арифметики, пройдите курс в Академии Хана.
Как мы уже сказали целые числа по модулю
— это поле, поэтому все перечисленные выше свойства сохраняются. Учтите, что требование того, чтобы было простым числом, очень важно! Множество целых чисел по модулю 4 не является полем: 2 не имеет мультипликативной инверсии (т.е. уравнение не имеет решений).Деление по модулю p
Скоро мы определим эллиптические кривые для
, но прежде нам нужно чётко понимать, что означает над . Попросту говоря: , или, прямым текстом, в числителе и в знаменателе равно раз обратная величина . Это нас не удивляет, но даёт нам простой способ выполнения деления: найти обратную величину числа, а затем выполнить простое умножение.Вычисление обратного числа можно «просто» выполнить с помощью расширенного алгоритма Евклида, который в худшем случае имеет сложность
(или , если мы учитываем битовую длину).Мы не будем вдаваться в подробности расширенного алгоритма Евклида, это не входит в рамки статьи, но я представлю работающую реализацию на Python:
def extended_euclidean_algorithm(a, b):
"""
Возвращает кортеж из трёх элементов (gcd, x, y), такой, что
a * x + b * y == gcd, где gcd - наибольший
общий делитель a и b.
В этой функции реализуется расширенный алгоритм
Евклида и в худшем случае она выполняется O(log b).
"""
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = b, a
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
return old_r, old_s, old_t
def inverse_of(n, p):
"""
Возвращает обратную величину
n по модулю p.
Эта функция возвращает такое целое число m, при котором
(n * m) % p == 1.
"""
gcd, x, y = extended_euclidean_algorithm(n, p)
assert (n * x + p * y) % p == gcd
if gcd != 1:
# Или n равно 0, или p не является простым.
raise ValueError(
'{} has no multiplicative inverse '
'modulo {}'.format(n, p))
else:
return x % p
Эллиптические кривые над
Теперь у нас есть все необходимые элементы для ограничения эллиптических кривых полем
. Множество точек, которые в предыдущей части имели следующий вид: теперь превращаются в:
где 0 — по-прежнему точка в бесконечности, а
и — два целых числа в .
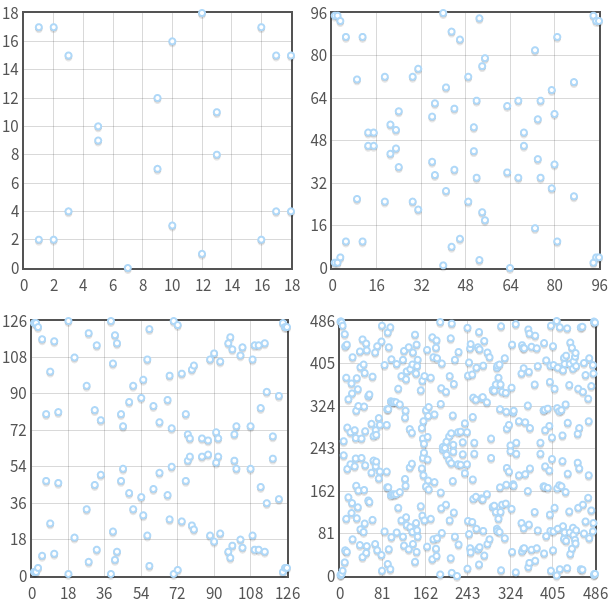
Кривая
с . Заметьте, что для каждого существует максимум две точки. Также заметьте симметрию относительно .
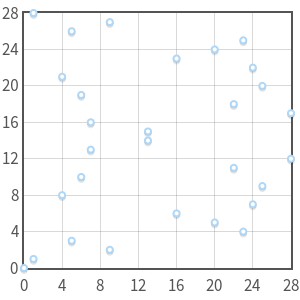
Кривая
— особая и имеет тройную точку в . Она не является истинной эллиптической кривой.То, что раньше было непрерывной кривой, теперь стало множеством отдельных точек на плоскости
. Но можно доказать, что несмотря на ограничение области определения, эллиптические кривые над всё равно создают абелеву группу.Сложение точек
Очевидно, что нам нужно немного изменить определение сложения, чтобы оно работало для
. Для вещественных чисел мы сказали, что сумма трёх точек на одной прямой равна нулю ( ). Мы можем сохранить это определение, но что значит расположение трёх точек на одной прямой над ?
Можно сказать, что три точки находятся на одной прямой, если существует прямая, соединяющая их. Разумеется, прямые над
отличаются от прямых над . Можно сказать, что прямая над — это множество точек , удовлетворяющих уравнению (это стандартное уравнение прямой с добавленной частью " ").
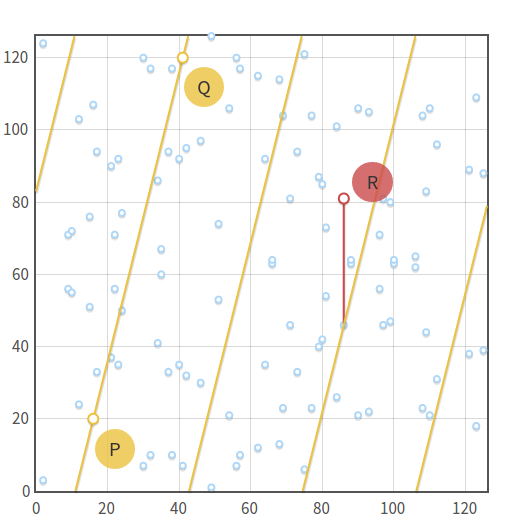
Сложение точек для кривой
, при и . Заметьте, как соединяющая точки прямая «повторяет» себя на плоскости.Учитывая то, что мы по-прежнему находимся в группе, сложение точек сохраняет уже известные нам свойства:
- (из определения единичного элемента).
-
Для обратная величина — это точка, имеющая ту же абсциссу, но обратную ординату. Или, если угодно, . Например, если кривая над имеет точку , то обратной величиной будет . -
Кроме того, (из определения обратной величины).
Алгебраическая сумма
Уравнения для выполнения сложений точек в точности такие же, как в предыдущей части, за исключением того, что нам нужно добавлять в конце каждого выражения "
". Поэтому, если , и , то можно вычислить следующим способом:
Если
, то наклон принимает форму: Иначе, если
, мы получаем: Уравнения не изменились, и это не совпадение: на самом деле, эти уравнения работают над любым полем, и над конечным, и над бесконечным (за исключением
и , которые являются особыми случаями). Я чувствую, что это нужно объяснить. Но есть проблема: для доказательств группового закона обычно требуются сложные математические понятия. Однако я нашёл доказательство Стефана Фридла в котором используются только простейшие концепции. Прочитайте его, если вам интересно, почему эти уравнения работают (почти) над любым полем.Вернёмся к кривым — мы не будем определять геометрический способ: на самом деле, с ним возникнут проблемы. Например, в предыдущей части мы сказали, что для вычисления
нам придётся взять касательную к кривой в . Но при отсутствии непрерывности слово «касательная» теряет всякий смысл. Мы можем найти способ обойти эту и другие проблемы, однако чисто геометрический способ будет слишком сложным и совершенно непрактичным.Вместо этого можно поэкспериментировать с интерактивным инструментом, написанным мной для выполнения сложений точек.