Файл: Геометрия пнінен алыптастырушы баалау тапсырмалар жинаы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 233
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Үш перпендикуляр туралы теореманы есептер
шығаруда қолданады
Ойлау дағдыларының Қолдану
деңгейі
Тапсырма 1
-
нүктесінен ABCD тіктөртбұрышының жазықтығына NB перпендикуляры түсірілген. Егер, AD =7, NA =24 болса, онда ND -ні табыңыз.
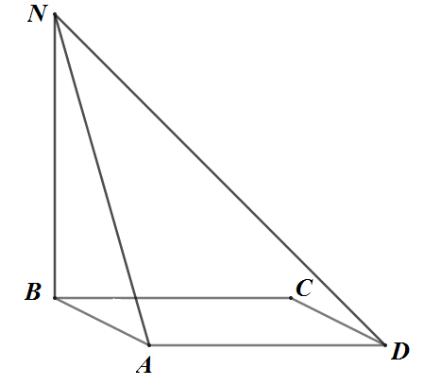
Дескриптор: Білім алушы
-
көлбеу проекциясын анықтайды; -
үш перпендикуляр туралы теореманы қолданады; -
тік бұрышты үшбұрыш жайлы қорытынды жасайды; -
Пифагор теоремасын қолданады; -
көлбеудің ұзындығын табады.
Тапсырма 2
-
түзуі жазықтығында жатыр, AO a , AK . K нүктесі жазықтығына, ал L нүктесі a түзуіне тиісті. Егер, OK = OL , KL 
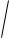 6, AOK 600 болса, онда AK -ның ұзындығын табыңыз.
6, AOK 600 болса, онда AK -ның ұзындығын табыңыз.
Дескриптор: Білім алушы
-
суреттен перпендикуляр мен көлбеуді анықтайды; -
үш перпендикуляр туралы теореманы қолданады; -
үшбұрыштың түрі жайлы қорытынды жасайды; -
Пифагор теоремасын қолданады; -
тікбұрышты үшбұрыштағы қатынасты қолданады;-
кесіндінің ұзындығын табады.
-
| | Бөлім: «Кеңістіктегі перпендикулярлық» |
| | |
| Оқу мақсаты | 10.3.5 Нүктеден жазықтыққа дейінгі және айқас түзулер |
| | арасындағы арақашықтықтарды таба білу; |
| Бағалау критерийі | Білім алушы |
Ойлау дағдыларының деңгейі
Нүктеден жазықтыққа дейінгі арақашықтықты
анықтайды
Айқас түзулер арасындағы арақашықтықтарды
табады
Қолдану
Тапсырма 1
ABCD ромбының диагональдары12см және16см.Ромб жазықтығынан тыс орналасқан O нүктесі ромбтың барлық қабырғаларынан 8см қашықтықта орналасқан. O нүктесінен ромб жазықтығына дейінгі арақашықтықты табыңыз.
Тапсырма 2
Тік бұрышы С төбесі болатын АВС тік бұрышты үшбұрышының АС катеті арқылы АВС жазықтығымен 300 бұрыш жасайтын жазықтығы жүргізілген. Егер АС=6 см, АВ=10 см болса, онда В нүктесінен жазықтығына дейінгі арақашықтықты табыңыз.
Дескриптор: Білім алушы
-
есеп шартына сәйкес сызбаны сызады; -
ромб диагональдарының қасиеттерін қолданады; -
Пифагор теоремасын қолданады; -
нүктеден жазықтыққа дейінгі арақашықтықты табады.
Тапсырма 3
ABCD квадратының жазықтығынаKDперпендикуляры жүргізілген.Квадраттыңқабырғасы 5 см. Келесі түзулердің арақашықтығын табыңыз:
-
AB және KD ;
-
KD жәнеAC;
Тапсырма 4
Кубтың қыры 8 см. Айқас болатын екі қырының орталарын қосатын кесіндінің ұзындығын табыңыз.
Дескриптор: Білім алушы
-
есеп шартына сәйкес сызбаны сызады; -
түзулердің өзара орналасуын анықтайды; -
ортақ перпендикулярды көрсетеді; -
түзулер арасындағы қашықтықты анықтайды.
| | Бөлім: «Кеңістіктегі перпендикулярлық» |
| | |
| Оқу мақсаты | 10.2.9 Кеңістіктегі екі түзу арасындағы бұрыш анықтамасын |
| | білу |
| | 10.2.10 Айқас түзулер арасындағы бұрыш пен олардың ортақ |
| | перпендикулярын сызбада кескіндей алу |
| Бағалау критерийі | Білім алушы |
| | Кеңістіктегі екі түзу арасындағы бұрыш |
| | анықтамасын қолданады |
| | Кеңістіктегі екі түзу арасындағы бұрышты |
| | анықтайды |
| Ойлау дағдыларының | Білу және түсіну |
| деңгейі | Қолдану |
Тапсырма 1
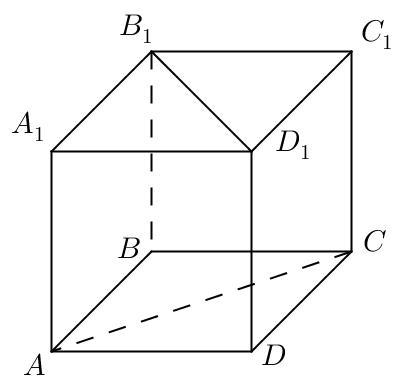
ABCDA1 B1C1 D1-куб.ACжәне B1 D1кесінділерін қамтитын түзулер арасындағы бұрыштытабыңыз. Жауабын градустық өлшеммен жазыңыз.
Дескриптор: Білім алушы
-
AC жәнеB1D1түзулерінің өзара орналасуын анықтайды;
-
екі түзу арасындағы бұрышты анықтайды; -
квадрат диагональдарының қасиетін қолданады; -
ізделінді бұрышты градуспен жазады.
Тапсырма 2
ABCD трапециясыныңADтабаны жазықтығында жатыр. B және C нүктелері арқылы
-
жазықтығын сәйкесінше E және F нүктелерінде қиятын параллель түзулер жүргізілген. Табыңыз:
а) EF және AB түзулері өзара қалай орналасқан?
b) егер ABC = 150° болса, онда EF және AB түзулері арасындағы бұрышты?
Дескриптор: Білім алушы
-
есеп шартына сәйкес сызбаны сызады; -
түзулердің өзара орналасуын анықтайды; -
түзулер арасындағы бұрышты анықтайды;
Тапсырма 3
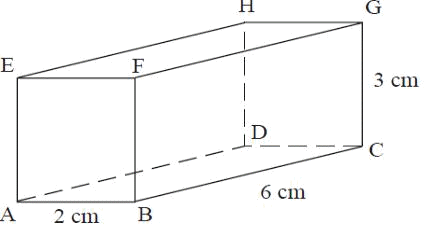
Сызбадан келесі түзулер арасындағы бұрышты кескіндеңіз және осы түзулерге ортақ перпендикуляр тұрғызыңыз:
-
HG және FB; -
AE мен DG; -
GK мен HD.
Дескриптор: Білім алушы
-
сызбадан түзулердің өзара орналасуын анықтайды; -
түзулер арасындағы бұрышты анықтайды; -
айқас түзулерге ортақ перпендикуляр тұрғызады.
| | Бөлім: «Кеңістіктегі перпендикулярлық» |
| | |
| Оқу мақсаты | 10.3.2 Түзу мен жазықтық арасындағы бұрыштың |
| | анықтамасын білу, кескіндей алу және оның шамасын |
| | табу |
Бағалау критерийі
Ойлау дағдыларының деңгейі
Білім алушы
-
Түзу мен жазықтық арасындағы бұрышты табады
-
Түзу мен жазықтық арасындағы бұрышты кескіндейді Білу және түсіну Қолдану
Тапсырма 1
Кубтың диагоналы 9 см. Табыңыз:
а) кубтың қырын;
-
кубтың диагоналы мен оның бір жағының арасындағы бұрыштың косинусын?
Дескриптор: Білім алушы
-
есеп шартына сәйкес сызбаны сызады; -
Пифагор теоремасын қолданады; -
кубтың қырын табады;
-
диагональ мен жақтың арасындағы бұрышты анықтайды; -
бұрыштың косинусын есептейді.
Тапсырма 2
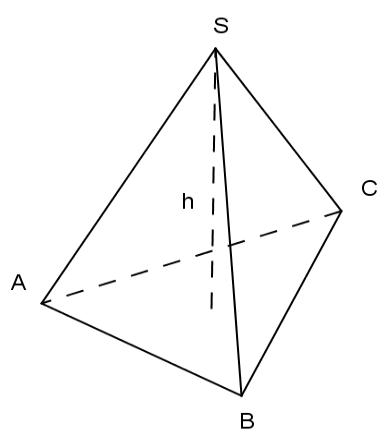
Суреттен SB түзуі мен ABC жазықтығы арасындағы бұрышты көрсетіңіз.
Тапсырма 3
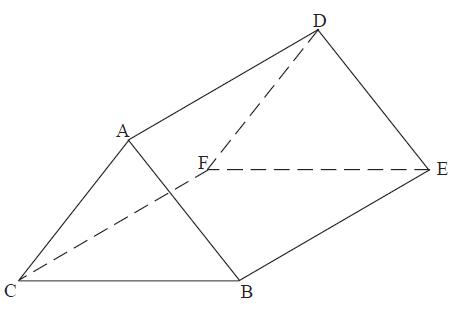
Суретте табандары дұрыс үшбұрыш болатын тік призма бейнеленген. Үшбұрыштың қабырғасы 5 см, призманың биіктігі 10 см. AF түзуі мен BCFE жазықтығы арасындағы бұрышты табыңыз.
Дескриптор: Білім алушы
-
перпендикуляр, көлбеу және көлбеудің проекциясын анықтайды; -
түзу мен жазықтық арасындағы бұрышты көрсетеді; -
түзу мен жазықтық арасындағы бұрышты есептейді.
| | Бөлім: «Кеңістіктегі перпендикулярлық» | |
| | | |
| Оқу мақсаты | 10.3.3 Жазықтықтар арасындағы бұрыштың (екіжақты | |
| | | бұрыш) анықтамасын білу, кескіндей алу және оның |
| | | шамасын табу |
| Бағалау критерийі | Білім алушы | |
| | | Екіжақты бұрышты анықтайды |
| | | Екіжақты бұрышты бейнелейді |
| Ойлау дағдыларының | Білу және түсіну | |
| деңгейі | Қолдану | |
Тапсырма 1
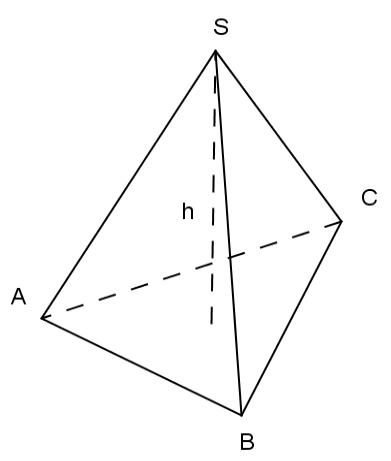
Суреттен SAC және ABC жазықтықтары арасындағы бұрышты бейнелеп көрсетіңіз.
Тапсырма 2
Суретте табандары дұрыс үшбұрыш болатын тік призма бейнеленген. Үшбұрыштың қабырғасы 5 см, призманың биіктігі 10 см. AЕF және BCFE жазықтықтары арасындағы бұрышты табыңыз.

Дескриптор:
Білім алушы
- екі жазықтыққа
анықтайды;
ортақ
түзуді
-
түзуге перпендикулярлар жүргізеді; -
жазықтықтар арасындағы бұрышты бейнелейді; -
жазықтықтар арасындағы бұрышты есептейді.
| | Бөлім: «Кеңістіктегі перпендикулярлық» |
| | |
| Оқу мақсаты | 10.3.4 Жазықтықтардың перпендикулярлық белгісі мен |
| | қасиетін білу және оларды есептер шығаруда қолдану |
| Бағалау критерийі | Білім алушы |
| | Жазықтықтардың перпендикулярлық белгісі мен |
| | қасиетін қолданады; |
| | Жазықтықтардың перпендикулярлық белгісі мен |
| | қасиетін есептер шығаруда қолданады |
| Ойлау дағдыларының | Білу және түсіну |
| деңгейі | Қолдану |
Тапсырма 1
Екіжақты бұрыштың қырына перпендикуляр жазықтық оның жақтарына да перпендикуляр болатынын көрсетіңіз.
Тапсырма 2
Әр фигурадан перпендикуляр жазықтықтар жұбын көрсетіңіз. Жазықтықтардың перпендикулярлығының белгісімен негіздеңіз.
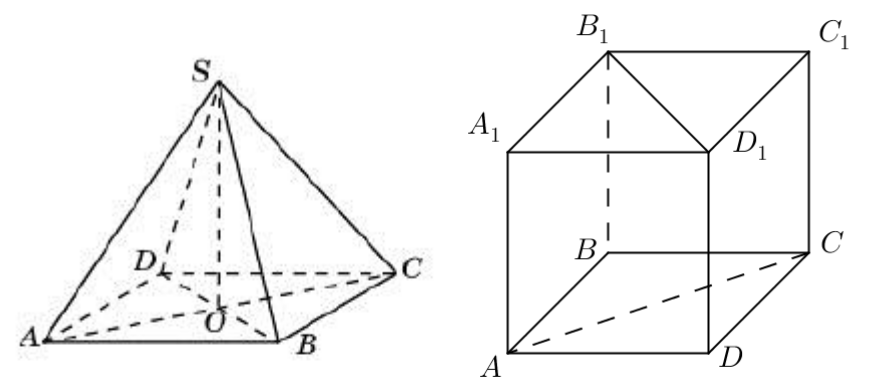
Дескриптор: Білім алушы
-
жазықтықтардың перпендикулярлық белгісін қолданады; -
тұжырымды дәлелдейді; -
перпендикуляр жазықтықтар жұбын көрсетеді.
Тапсырма 3
-
және β жазықтықтары өзара перпендикуляр және a түзуі бойымен қиылысады. М нүктесінен осы жазықтықтарға МА және МВ перпендикулярлары жүргізілген. а түзуі АМВ жазықтығын C нүктесінде қияды. АСВМ төртбұрышы тіктөртбұрыш болатынын дәлелдеңіз.
Дескриптор: Білім алушы
-
тапсырмаға сәйкес сызбаны сызады; -
перпендикуляр жазықтықтардың қасиетін қолданады; -
АСВМ төртбұрышы тіктөртбұрыш болатынын дәлелдейді.
Тапсырма 4
DE түзуі ABCD тіктөртбұрыш жазықтығына перпендикуляр.(ADE) жазықтығының(EDC) жазықтығына перпендикуляр болатынын дәлелдеңіз.
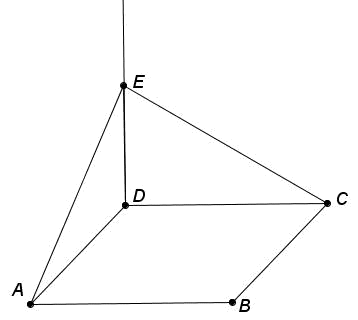
Дескриптор: Білім алушы
-
жазықтықтардың перпендикулярлық белгісі мен қасиетін қолданады;
-
жазықтықтардың перпендикулярлығын дәлелдейді.
Тапсырма 5
АDЕ үшбұрыш жазықтығы мен ABCD квадрат жазықтығы өзара перпендикуляр. ED кесіндісінің ұзындығы6см.Квадраттың қабырғасы4см. Е нүктесіненквадраттың В төбесіне дейінгі арақашықтықты табыңыз.
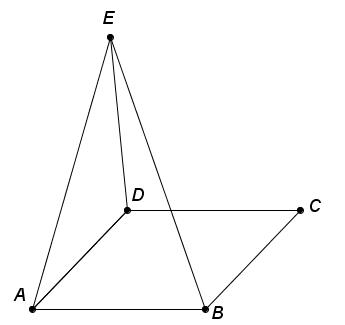
Дескриптор: Білім алушы
-
EDB үшбұрышын толықтырады;
-
жазықтықтардың перпендикулярлық белгісі мен қасиетін қолданады;
-
EDB үшбұрышының тік бұрышты үшбұрыш болатынын дәлелдейді; -
DB катетін табады; -
ЕВ ұзындығын табады.
-
тоқсан