Файл: Геометрия пнінен алыптастырушы баалау тапсырмалар жинаы.doc

Скачать файл (1,06Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 239

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Бөлім: «Кеңістіктегі перпендикулярлық»

Оқу мақсаты Бағалау критерийі
10.1.2 Тікбұрышты параллелепипед анықтамасын және

қасиеттерін білу
Білім алушы

Ойлау дағдыларының деңгейі

 тікбұрышты параллелепипед
қасиеттерін қолданады

Білу және түсіну
анықтамасын
және

Тапсырма 1

a) Тікбұрышты параллелепипедтің анықтамасын жазыңыз.
b) Бос орынды толтырыңыз:

Тікбұрышты параллелепипедтің ____ тікбұрышты жағы, ____ төбесі, әр төбеде ____ қырдан
тоғысады, барлығы ___ қыры бар.
Тапсырма 2

Тұжырымдап, жазыңыз:

тікбұрышты параллелепипедтің диагоналына қатысты қасиетін;.
тікбұрышты параллелепипедтің көлеміне қатысты қасиетін;

с) тікбұрышты параллелепипед көлеміне қатысты қасиетінің салдарын.
Дескриптор: Білім алушы:

тікбұрышты параллелепипед анықтамасын жазады;
тікбұрышты параллелепипед элементтерін ажыратады;
тікбұрышты параллелепипедтің қасиеттерін тұжырымдайды.

Бөлім: «Кеңістіктегі перпендикулярлық»

Оқу мақсаты
Бағалау критерийі

Ойлау дағдыларының деңгейі
10.3.7 Тікбұрышты параллелепипедтің қасиеттерін қорытып шығару және есептер шығаруда қолдану
Білім алушы

тікбұрышты параллелепипедтің қасиеттерін қорытып шығарады

оларды есептер шығаруда қолданады

Білу және түсіну
Қолдану

Тапсырма 1

Дәлелдеңіз:

тікбұрышты параллелепипедтің диагоналына қатысты қасиетін;

тікбұрышты параллелепипедтің көлеміне қатысты қасиетін;
тікбұрышты параллелепипед көлеміне қатысты қасиетінің салдарын.

Дескриптор: Білім алушы:

тікбұрышты параллелепипедті сызады, белгілеулер енгізеді;
тікбұрышты параллелепипедтің диагоналын жүргізеді;
Пифагор теоремасын қолданады;

тікбұрышты параллелепипедтің диагоналына қатысты қасиетін қорытып шығарады;

тікбұрышты параллелепипедтің өлшемдерін енгізеді;

тікбұрышты параллелепипедтің көлеміне қатысты қасиетін қорытып шығарады;

тікбұрышты параллелепипед көлеміне қатысты қасиетінің салдарын қорытып шығарады.

Тапсырма 2

Егер тікбұрышты параллелепипедтің өлшемдері: 2; 3 және 6 болса,онда диагоналын есептеңіз.

Тікбұрышты параллелепипедтің өлшемдері 4; 16 және 27, ал оның көлемі кубтың көлеміне тең. Кубтың көлемін табыңыз.

Дескриптор: Білім алушы:

тікбұрышты параллелепипедтің диагоналына қатысты қасиетін қолданады;

тікбұрышты параллелепипед диагоналын есептейді;
тікбұрышты параллелепипед көлеміне қатысты қасиетін қолданады;
кубтың қырын табады;
кубтың көлемін табады.

	Бөлім: «Кеңістіктегі перпендикулярлық»

Оқу мақсаты	10.2.11 Жазық фигураның ортогональ проекциясын
	жазықтықта салу
Бағалау критерийі	Білім алушы

 жазық фигураның ортогональ проекциясын жазықтықта салады
Ойлау дағдыларының Білу және түсіну
деңгейі
Тапсырма
Келесі фигуралардың жазықтықтағы ортогональ проекцияларын салыңыз:
a) үшбұрыш;

квадрат;

c) параллелограмм;

трапеция.

Дескриптор: Білім алушы:

үшбұрыштың ортогональ проекциясын салады;
квадраттың ортогональ проекциясын салады;
параллелограмның ортогональ проекциясын салады;
трапецияның ортогональ проекциясын жазықтықта салады.

	Бөлім: «Кеңістіктегі перпендикулярлық»

Оқу мақсаты	10.3.6 Жазық фигураның жазықтыққа ортогональ
	проекциясы ауданының формуласын білу және оны
	есептер шығаруда қолдану;

Бағалау критерийі

Ойлау дағдыларының деңгейі
Тапсырма 1
Білім алушы

жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын есептер шығаруда қолданады

Білу және түсіну

Қолдану

Қабырғалары a және b, ал олардың арасындағы бұрыш 45⁰-қа тең болатын параллелограмм – ромбының ортогональ проекциясы. Ромбының бір бұрышы 120⁰. Егер ромб пен параллелограмм жазықтықтарының арасындағы бұрыш 60⁰-қа тең болса, онда ромбының қабырғасын табыңыз.
Дескриптор: Білім алушы

есеп шартына сәйкес сызбасын салады;
параллелограмның ауданын табады;

жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын қолданады;

ромбтың ауданын табады;
Пифагор теоремасын қолданады;
тікбұрышты үшбұрыштағы қатынастарды қолданады;
ромб қабырғасын табады.

Тапсырма 2

АВС үшбұрышының ауданы18,ал оныңαжазықтығындағы проекциясының ауданы9

3 .
АВС үшбұрышы менαжазықтығының арасындағы бұрышты табыңыз.
Дескриптор: Білім алушы

ортогональ проекциясы ауданының формуласын қолданады;
үшбұрыш пен жазықтық арасындағы бұрышты табады.

Бөлім: «Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»

Оқу мақсаты Бағалау критерийі
10.4.1 Кеңістіктегі вектор, вектордың ұзындығы, тең

векторлар анықтамаларын білу
Білім алушы

Ойлау дағдыларының деңгейі

 кеңістіктегі вектор, вектордың ұзындығы, тең

векторлар анықтамаларын қолданады;

 Вектордың ұзындығын есептейді

Білу және түсіну
Қолдану

Тапсырма 1

Келесі терминдердің анықтамаларын аяқтаңыз:

кеңістіктегі вектор деп ....
вектордың ұзындығы деп ....
тең векторлар деп ...

Дескриптор: Білім алушы

кеңістіктегі вектор анықтамасын жазады;
вектордың ұзындығы анықтамасын жазады;
тең векторлар анықтамасын жазады.

Тапсырма 2
ABCDMNKL параллелограмы берілген.Параллелограмды сызып,сызбадан тең векторлардыанықтаңыз.
Дескриптор: Білім алушы

параллелограмды сызады;
сызбадан тең векторларды анықтайды;
векторлардың теңдігін жазады.

Тапсырма 3

Табыңыз:

а2;3;1векторының ұзындығын;

егер, А(0;2;4), В(3;-5;2) нүктелері берілсе, онда АВ векторының ұзындығын.

Дескриптор: Білім алушы

вектор ұзындығының формуласын қолданады;
вектор ұзындығын есептейді.

Бөлім: «Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»

Оқу мақсаты	10.4.2 Векторларды қосу және векторды санға көбейтуді
	орындау
Бағалау критерийі	Білім алушы
	 векторларды қосу және азайту ережесін қолданады;
	 векторды санға көбейтеді.
Ойлау дағдыларының	Қолдану
деңгейі
Тапсырма 1
		1
Егер a(2;3;0), b(0;3;4), c(5;4;2) болса, онда p  3a 			b	 c векторының
Егер a(2;3;0), b(0;3;4), c(5;4;2) болса, онда p  3a 		2	b	 c векторының

координаталарын табыңыз.
Дескриптор: Білім алушы

векторды санға көбейту ережесін қолданады;
векторларға амалдар қолданады;
вектордың координаталарын табады.

Тапсырма 2

Бір жазықтықта жатпайтын a , b		және c векторларының қосындысын бейнелеңіз.

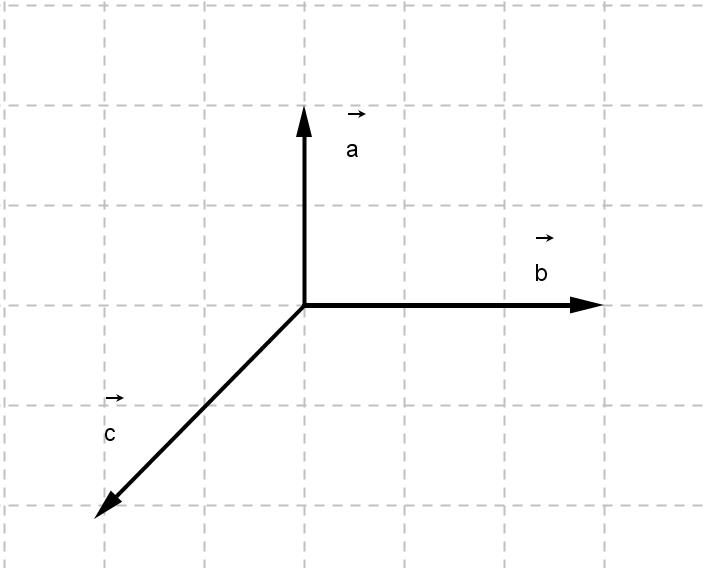
Дескриптор: Білім алушы

параллелепипедті тұрғызады;
параллелепипед ережесін қолданады;

үш вектордың қосындысынан пайда болған векторды бейнелейді.

Бөлім: «Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»

Оқу мақсаты Бағалау критерийі
10.4.3 Кеңістіктегі коллинеар және компланар векторлардың

анықтамаларын білу;
Білім алушы

 кеңістіктегі коллинеар векторлар анықтамасын

қолданады

 кеңістіктегі компланар векторлар анықтамасын

қолданады

Ойлау дағдыларының деңгейі
Білу және түсіну

Тапсырма

Кеңістіктегі:

коллинеар;
компланар векторлардың анықтамаларын жазыңыз.

Дескриптор: Білім алушы

кеңістіктегі коллинеар векторлар анықтамасын жазады;
кеңістіктегі компланар векторлар анықтамасын жазады.

Бөлім: «Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»

Оқу мақсаты Бағалау критерийі
10.4.5 Кеңістіктегі тікбұрышты координаталар жүйесі

анықтамасын білу және оны кескіндей алу

10.4.6 Кеңістіктегі нүктені оның координаталары бойынша

тікбұрышты координаталар жүйесінде кескіндеу
Білім алушы

Ойлау дағдыларының деңгейі

 Кеңістіктегі тікбұрышты координаталар жүйесін

кескіндейді;

 Кеңістіктегі нүктені оның координаталары бойынша

тікбұрышты координаталар жүйесінде кескіндейді
Қолдану

Тапсырма 1
Бос орынды толтырыңыз:

A(0; 2; 0)нүктесі_______________осіне тиісті;

B(3;0; 4)нүктесі_______________тиісті;

C(0; 0; n)нүктесі_______________тиісті;

D(t; 0; 0)нүктесі_______________тиісті.

Дескриптор: Білім алушы

абсцисса осіне тиісті нүктені анықтайды;
ордината осіне тиісті нүктені анықтайды;
аппликатаа осіне тиісті нүктені анықтайды;
жазықтыққа тиісті нүктені анықтайды.

Тапсырма 2

Кеңістіктегі тікбұрышты координаталар жүйесінде келесі нүктелерді бейнелеңіз:

A(1;4;3), B(3;0;2), C(0;0;6), D(5;2;0).
Дескриптор: Білім алушы