Добавлен: 23.11.2023
Просмотров: 1680
Скачиваний: 13
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
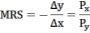
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
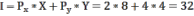
где
I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача 19.
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара - Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) - TU(1)=30 – 19 = 11
MU(3)= TU(3) - TU(2)=38 – 30 = 8
MU(4)= TU(4) - TU(3)=43 – 38=5
MU(5)= TU(5) - TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) - TU(2)=39 – 32=7
MU(4)= TU(4) - TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача 20.
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =...=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 =
= 769,96582
Задача 21.
В таблице представлены следующие данные о предельной полезности двух благ.
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
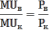
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
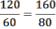
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача 22.
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед.
Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
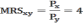
Запишем бюджетное ограничение:
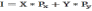
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
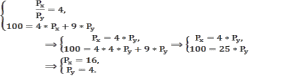
Задача 23.
Потребитель имеет функцию полезности:
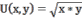
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
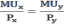
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
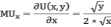
Аналогично находим предельную полезность товара y:
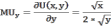
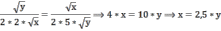
Далее воспользуемся бюджетным ограничением:
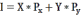
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
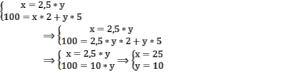
При х = 25 и у = 10 общая полезность достигнет максимума:
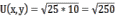
Задача 24.
Фирма имеет кривую спроса:
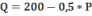
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Решение:
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR - marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
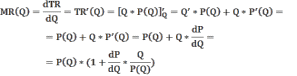
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
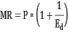
Определим эластичность спроса по цене:
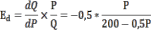
При P=100
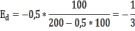
Тогда:
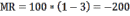
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача 25.
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Решение:
а) Выручка фирмы рассчитывается по формуле:
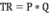
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:
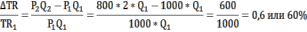
Таким образом, выручка фирмы увеличилась на 60 %.
б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:
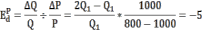
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.
Задача 26.
Функция задана уравнением
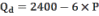
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
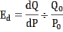
Где
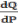– производная функции спроса в этой точке.
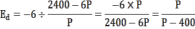
б)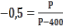
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача 27.
Является ли спрос на товар эластичным, если известно:
Решение:
При значительных колебаниях цены (более 10%) рекомендуется использовать коэффициент дуговой эластичности:
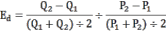
Решение:
В точке оптимума выполняется равенство:
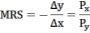
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
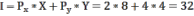
где
I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача 19.
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||||
| TU | MU | TU | MU | TU | MU | |||
| 1 | ... | 20 | 19 | ... | 22 | ... | ||
| 2 | ... | 15 | 30 | ... | ... | 10 | ||
| 3 | ... | 12 | 38 | ... | 39 | ... | ||
| 4 | ... | 8 | 43 | ... | 44 | ... | ||
| 5 | ... | 6 | 45 | ... | ... | 3 | ||
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара - Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) - TU(1)=30 – 19 = 11
MU(3)= TU(3) - TU(2)=38 – 30 = 8
MU(4)= TU(4) - TU(3)=43 – 38=5
MU(5)= TU(5) - TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) - TU(2)=39 – 32=7
MU(4)= TU(4) - TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
| Количество товара | А | В | С | ||||
| TU | MU | TU | MU | TU | MU | ||
| 1 | 20 | 20 | 19 | 19 | 22 | 22 | |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 | |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 | |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 | |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 | |
Заполним пропуски в таблице:
Задача 20.
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =...=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 =
= 769,96582
Задача 21.
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
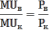
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
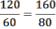
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача 22.
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед.
Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
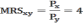
Запишем бюджетное ограничение:
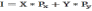
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
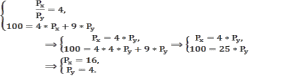
Задача 23.
Потребитель имеет функцию полезности:
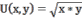
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
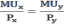
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
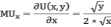
Аналогично находим предельную полезность товара y:
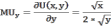
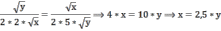
Далее воспользуемся бюджетным ограничением:
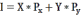
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
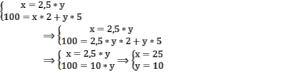
При х = 25 и у = 10 общая полезность достигнет максимума:
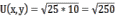
Задача 24.
Фирма имеет кривую спроса:
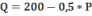
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Решение:
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR - marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
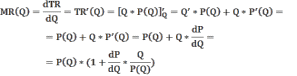
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
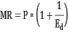
Определим эластичность спроса по цене:
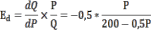
При P=100
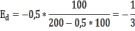
Тогда:
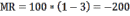
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача 25.
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Решение:
а) Выручка фирмы рассчитывается по формуле:
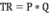
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:
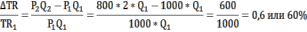
Таким образом, выручка фирмы увеличилась на 60 %.
б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:
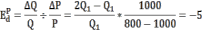
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.
Задача 26.
Функция задана уравнением
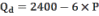
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
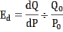
Где
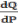– производная функции спроса в этой точке.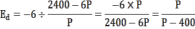 б)
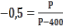
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача 27.
| Цена, руб. | Объём спроса |
| 3500 | 500 |
| 4000 | 440 |
Является ли спрос на товар эластичным, если известно:
Решение:
При значительных колебаниях цены (более 10%) рекомендуется использовать коэффициент дуговой эластичности: