Файл: Банк задач и упражнений по экономике.docx

П’ = (– Q² + 30Q – 100)’ = – 2Q + 30

– 2Q + 30 = 0

Q = 15

Итак, выпуск Q = 15 обеспечивает максимум прибыли. Найдём величину прибыли, подставив это значение в функцию прибыли.

П = – Q² + 30Q – 100 = – 225 + 30 × 15 – 100 = 125

Делаем вывод: при Q = 10, когда средние затраты минимальны, П = 100;
при Q = 15, когда прибыль максимальна, она равна 125. Следовательно, недополученная прибыль будет равна 25.


Задача 54.

На четырех одинаковых по площади земельных участках выращивается виноград. 
Природно-экономические показатели этих земель характеризуют следующие данные:

Участок	I	II	III	IV
Расходы выращивания, долл	2000	2600	3600	4000
Валовой сбор, т	8	12	20	16
Расстояние до рынка сбыта, км	10	50	100	105

Транспортный тариф перевозок 1 т на расстояние в 1 км 0,4

Величина абсолютной ренты, 300.долл.

Определите:

цену каждого участка, если известно, что общественная норма прибыли - 15%, а ссудный процент на одолженный у банка капитал равен 5% годовых.

Виды ренты способствуют формированию цен на землю?

Существует ли дифференциальная рента на I участке?

Существует ли дифференциальная рента на II участке?

Какие участки обеспечивают этот вид ренты?

Назовите причины которые, на ваш взгляд обусловливают разное качество каждого земельного участка?

Участки имеют большую производительность?

Ответы обоснуйте экономичным анализом.

 Решение:

В основе рыночных цен на сельскохозяйственную продукцию лежит стоимость единицы продукции, полученной с худших земельных участков. Поэтому вся продукция со всех земельных участков будет продаваться по цене, соответствующей стоимости продукции с худшего земельного участка. Худшим земельным участком будет тот, на котором затраты производства 1 т винограда самые высокие.

Для простоты анализа составим таблицу расчётных данных:

---

Участок земли	Издержки производства, долл.	Общественная нормы прибыли, %	Стоимость всей продукции, долл.	Валовый сбор, т	Абсолютная рента, долл.
А	1	2	3	4	5
I	2000 + 8 × 10 × 0,4 = 2032	15	2032 × 1,15 = 2336,8	8	300
II	2600 + 12 × 50 × 0,4 = 2840	15	2840 × 1,15 = 3266	12	300
III	3600 + 20 × 100 × 0,4 = 4400	15	4400 × 1,15 = 5060	20	300
IV	4000 + 16 × 105 × 0,4 = 4672	15	4672 × 1,15 = 5372,8	16	300

 Продолжение таблицы

Участок земли	Индивидуальная стоимость, долл.		Общественная стоимость, долл. (рыночная)		Рента дифференциальная, долл.		Совокупная рента, R
	Всего урожая, долл.	1 т, долл.	1 т, долл.	Всего урожая, долл.
A	6 = ст.3 + ст.5	7 = ст.6 / ст.4	8 = max {ст.7}	9 = ст.4 × ст.8		10 = ст.9 - ст.6		11 = ст.5 + ст.10
I	2636,8	329,60	354,55	2836,4		199,6		499,6
II	3566,0	297,17	354,55	4254,6		688,6		988,6
III	5360,0	268,00	354,55	7091,0		1731,0		2031,0
IV	5672,8	354,55	354,55	5672,8		0		300

---

Издержки производства включают в данной задаче расходы выращивания и транспортные расходы.

Найдём цену земли.

Субъект, желающий купить земельный участок, должен учесть альтернативные варианты вложения денег и получения дохода. Субъект выбирает: положить деньги в банк или купить земельный участок. Поэтому при всех неизменных условиях цену земли можно выразить следующей формулой:



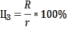
где

R – размер арендной платы (рента),
r – величина ссудного процента или процентная ставка,

Размер арендной платы = Абсолютная рента + Дифференциальная рента +

+ Процент на капитал

Так как в задании не сказано осуществлялись ли ранее капиталовложения в постройки и сооружения, размер арендной платы и размер совокупной ренты будут совпадать. В противном случае арендная плата на ряду с рентой включает в себя выплату процента на вложенный капитал и амортизационные отчисления на вложенный капитал.

Таким образом, для нашего задания:

Размер арендной платы = Абсолютная рента + Дифференциальная рента =

= Совокупная рента  

Абсолютная рента получается собственниками земли абсолютно со всех земельных участков и абсолютно одинаковой величины, если размеры земельных участков одинаковы.

В условии задания сказано, что все четыре участка одинаковы по площади и  величина абсолютной ренты равна 300 долл.

Дифференциальная рента будет получена собственниками земли только со средних и лучших участков земли, как по качеству и плодородию почвы, так и по месторасположению. Участки, обладающие дифференциальной рентой: I, II и III.

IV участок земли будет иметь только абсолютную ренту. Поэтому виды ренты будут способствовать формированию цен на землю. Цена земли IV участка будет зависеть только от величины абсолютной ренты и величины ссудного капитала, в отличии от I, II и III участка, где цена зависит ещё и от величины дифференциальной ренты.

Совокупная рента - это избыточная прибыль которую присваивают собственники земли.

Можно сказать, что собственник III участка, за счёт наилучшей его производительности получит наибольшую избыточную прибыль.

Рассчитаем цены земельных участков.

Цена I участка земли:

---

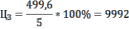
 долл.

Цена II участка земли:

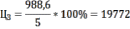 долл.

Цена III участка земли:

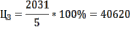 долл.

Цена VI участка земли:

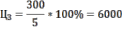 долл.

Задача 55.

Фирма находится в условиях совершенной конкуренции на рынке данного товара и труда. Ее производственная функция имеет вид

Q = 120 × L – 2 × L 2

в интервале использования труда от 12 до 30 единиц. Ставка заработной платы равна 60 ден. ед., а цена товара 8 ден. ед. Определить оптимальный для фирмы выпуск продукции.

 Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC

где

MRP_L – предельная доходность труда,

МIC – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда.

Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае:

Р = МR

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC = ω,

где

ω – ставка заработной платы

Таким образом, для совершенно конкурентной во всех отношениях фирмы условие максимизации прибыли при покупке фактора производства будет иметь вид:

P × MP_L= ω

Продифференцируем производственную функцию и найдём предельный продукт труда (MP_L) по формуле:



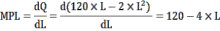
Подставим это выражение в условие максимизации прибыли и найдём количество нанимаемого труда:

8 × (120 – 4 × L) = 60

960 – 32 × L = 60

900 = 32 × L

L = 28,125

Оптимальный для фирмы выпуск продукции будет равен:

---

Q = 120 × 28,125 – 2 × 28,125 ² = 1793

Задача 56.

Фирма, являющаяся монополистом на рынке блага и совершенным конкурентом на рынке фактора, производит продукцию по технологии

Q = 2 × L.

Цена фактора 8 ден. ед. Функция спроса на продукцию монополиста

Qd = 12 – Р.

Определить количество закупаемого фактора, объем выпуска продукции и цену продукции, максимизирующие прибыль монополии.


Решение: 

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC_L

где

MRP_L – предельная доходность труда,

МIC_L – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма является монополистом на рынке блага и совершенным конкурентом на рынке труда.

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC = ω,

где

ω – ставка заработной платы

Таким образом, условие максимизации прибыли при покупке фактора производства будет иметь вид:

MR × MP_L= ω

Найдём предельную выручку как производную от общей выручки:

MR = TR’ = (P×Q)’ = (12 × Q – Q²)’=12 – 2 × Q

где

Р = 12 – Q – обратная функция спроса.

По условию Q = 2 × L, следовательно, MR = 12 – 4 × L

Найдём предельный продукт труда:



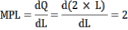
Воспользуемся условием максимизации прибыли и найдём количество закупаемого фактора :

(12 – 4 × L) × 2 = 8

L = 2

Тогда объем выпуска продукции Q = 4.

Цену продукции найдём из обратной функции спроса:

Р = 12 – Q =12 – 4 = 8

---