ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 385
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 280. Действие дифракционной решетки: S — ярко освещенная щель, параллельная штрихам решетки, L1 — линза, в фокальной плоскости которой расположена щель, R — дифракционная решетка, L2 — линза, дающая совместно с L1 изображение S на экране М, S0 — изображение щели S с помощью неотклоненных лучей (максимум нулевого порядка), S1, S'1 — изображения щели S с помощью отклоненных решеткой лучей (максимумы первого порядка), S2, S'2 — изображения щели S с помощью отклоненных решеткой лучей (максимумы второго порядка) и т. д.
если нанести царапины на поверхность металлического зеркала. В этих решетках чередуются полоски, правильно отражающие свет, и царапины, разбрасывающие свет во все стороны. Такие решетки называются отражательными. Сумму ширины прозрачной (отражающей) и непрозрачной (рассеивающей) полоски принято называть периодом решетки d. В лучших современных решетках наносят до 1800 штрихов на 1 мм, так что период решетки может быть около 0,8 мкм.
Направим на решетку перпендикулярно к ее поверхности пучок параллельных лучей. Для этого можно ярко осветить узкую щель S, расположенную в фокальной плоскости собирающей линзы L1(рис. 280). Свет, проходя через узкие прозрачные полоски решетки RR, испытывает дифракцию, отклоняясь в стороны от своего первоначального направления. При помощи второй линзы L2получим на экране М изображение щели S. Так как вследствие дифракции лучи от решетки падают на линзу L2по разным направлениям, то изображения щели S должны расположиться в разных местах экрана. Однако благодаря взаимной интерференции отклоненных пучков некоторые из этих изображений будут отсутствовать (минимумы), а другие будут особенно сильны (максимумы S0, S1, S'1, S2,S'2...).
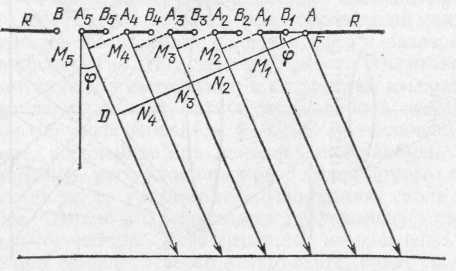
Рис. 281. К теории дифракционной решетки
Результат такой интерференции можно рассчитать, пользуясь рис. 281, где изображены несколько рядом расположенных прозрачных участков решетки. Предположим, что на решетку падает монохроматический свет длины волны . Пусть фронт падающей волны совпадает с АВ (плоскостью решетки), т. е. свет падает перпендикулярно к решетке. В результате дифракции света на выходе из решетки будут наблюдаться световые волны, распространяющиеся по всевозможным направлениям. Рассмотрим волны, распространяющиеся от решетки по направлению, составляющему угол с нормалью к плоскости решетки. Разности хода лучей, идущих от соответствующих точек отверстий, например от правых краев (точки А, A1, A2, А3, . . .), от левых краев (точки B1, B2,B3,B4 . . .) или от середин отверстий и т. д., имеют, конечно, одно и то же значение. Эти разности равны
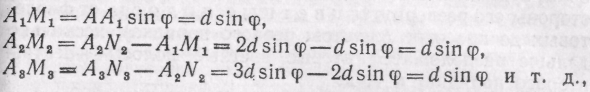
где d=AA1=A1A2=A2A3есть период решетки. Для того чтобы все пучки усиливали друг друга, необходимо, чтобы dsin равнялось целому числу длин волн , т. е.
где n —целое число. Таким образом, условие (135.1) есть условие взаимного усиления всех пучков, прошедших через отверстия решетки. Это условие позволяет определить те значения угла , т. е. те направления, по которым будут наблюдаться максимумы света длины волны . Эти углы найдем из формулы
давая nразличные целые значения: 0, ±1, ±2, ±3 и т. д.
§ 136. Дифракционная решетка как спектральный прибор.
Из формулы (135.2) следует, что для данной длины волны может наблюдаться несколько максимумов. Направление, соответствующее n=0, есть =0; это — направление первоначального пучка. Соответствующий максимум носит название максимума нулевого порядка; на рис. 280 ему соответствует точка S0. При n=1 имеем: sin1=/d, при n
=—1, sin'1=—/d, т. е. имеются два максимума первого порядка, расположенных симметрично по обеим сторонам нулевого максимума (точки S1 и S'1на рис. 280). При n=±2 найдем sin2=2/dи sin'2=—2/d, т. е. два симметричных максимума второго порядка (точки S2 и S'2 на рис. 280), и т. д.
Отсюда непосредственно следует, что для волн разной длины положения максимумов нулевого порядка, соответствующие =0, совпадают, а положения максимумов первого, второго и т. д. порядков различны: чем больше , тем больше соответствующие . Таким образом, более длинные волны дают изображения щели, дальше расположенные от нулевого максимума. Если на щель S(рис. 280) падает сложный свет (например, белый), то в плоскости экрана ММ мы получим ряд цветных изображений щели, расположенных в порядке возрастающих длин волн. На месте нулевого максимума, где сходятся все длины волн, будем иметь изображение щели в белом свете, а по обе стороны его развернутся цветные полосы от фиолетовых до красных (спектры первого порядка); несколько дальше расположатся вторые цветные полосы (спектры второго порядка) и т. д.
Так как длина волны красного цвета около 760 нм, а фиолетового около 400 нм, то красный конец спектра второго порядка накладывается на спектр третьего порядка. Еще сильнее перекрываются спектры высших порядков. Рис. V (см. форзац) дает схематическое изображение спектра, полученное с помощью дифракционной решетки. Легко видеть, что этот рисунок, представляющий результаты опыта, подтверждает все полученные выше выводы.
Если период решетки dмал, то соответствующие значения велики; точно так же при малом dвелика и разность двух значений для волн различной длины. Таким образом, уменьшение периода решетки увеличивает угловое расстояние между максимумами различных длин волн. Если свет, падающий на щель, представляет смесь различных длин волн 1, 2, 3и т. д., то при помощи дифракционной решетки можно более или менее полно разделить эти длины волн. Чем больше общий размер решетки, т. е. чем больше полосок она содержит, тем выше качество решетки: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче) и улучшает разделение излучений близких длин волн (максимумы становятся резче).
Зная период дифракционной решетки
, можно ее использовать для определения длины световой волны, измерив угол , определяющий положение максимума данного порядка. В таком случае из соотношения dsin=nнайдем
Измерение длины световой волны при помощи дифракционных решеток принадлежит к числу наиболее точных.
§ 137. Изготовление дифракционных решеток. Хорошая дифракционная решетка должна обладать малым периодом и большим числом полосок. В современных хороших решетках число это превышает 100 000 (ширина решетки до 100 мм, число полосок до 1200 на 1 мм). Полоски должны быть строго параллельными между собой, и ширина полосок каждого сорта (прозрачных и непрозрачных) строго одинакова (равенство ширины прозрачной и непрозрачной полосок не обязательно). Существенно, чтобы период решетки dбыл постоянен.
Хорошие решетки получают, проводя тонким резцом параллельные штрихи на поверхности металлического зеркала (отражательной решетки), причем штрихи, разбрасывающие свет во все стороны, играют роль темных полосок, а нетронутые места зеркала — роль светлых. Для изготовления решетки, работающей на пропускание, можно прочертить штрихи на поверхности стеклянной пластинки *). Для изготовления решетки требуется первоклассная делительная машина. В настоящее время широкое применение находят дифракционные решетки, полученные в результате регистрации на специальных фотопластинках интерференционной картины, возникающей при интерференции двух плоских монохроматических световых волн, падающих под разными углами на плоскость фотопластинки.
§ 138. Дифракция при косом падении света на решетку. На рис, 280 изображена дифракция параллельного пучка лучей (плоская волна) в случае, когда падающий пучок перпендикулярен к плоскости решетки (угол падения равен нулю). Дифракция, конечно, будет наблюдаться и при косом падении света, когда угол падения равен а.
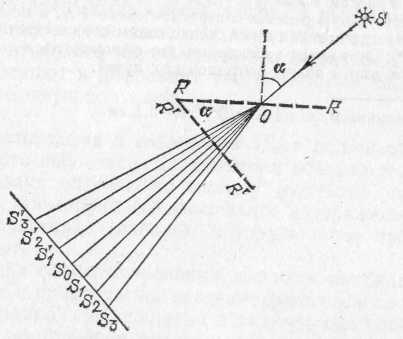
Рис. 282. Схематическое изображение дифракции при косом падения
светового пучка на решетку: SO — направление первичного пучка,
— угол падения,
RR — дифракционная решетка, R'R' — проекция
RR на направление, перпендикулярное к первичному пучку, OS0 —
направление на нулевой максимум, OS1 и OS'2 — направления на максимумы первого порядка, OS2 и OS'2 — направления на максимумы
второго порядка и т. д.
В этом случае дифракция происходит так, как если бы наша решетка была заменена другой, представляющей ее проекцию на направление, перпендикулярное к падающим лучам (рис. 282). Нулевой максимум будет, следовательно, лежать на продолжении первичного пучка, а пе-
*) Так как при прочерчивании штрихов по стеклу или металлу резец тупится, и поэтому трудно обеспечить равенство ширины штрихов, то хорошие решетки на стекле изготовляются редко. Прозрачные решетки изготовляют в виде отпечатков из специальных пластичных материалов с металлической (отражательной) решетки, Такие решетки (так называемые реплики) относительно недороги.
риодом будет служить величина d'=dcos. В тех случаях, когда а близко к 90° (скользящее падение), период, определяющий дифракционную картину, может быть гораздо меньше, чем период действительной решетки. Благодаря этому можно наблюдать дифракцию света на очень грубой решетке.
Взяв, например, металлическую линейку с миллиметровыми делениями и расположив ее весьма наклонно к лучам, идущим от волоска удаленной лампы накаливания (волосок должен располагаться параллельно штрихам решетки, играя роль освещенной щели), можно легко наблюдать дифракционные спектры разных порядков. Меняя поворотом линейки угол падения, можно видеть, как растягиваются спектры и увеличивается расстояние между порядками (т. е. уменьшается период) по мере приближения угла падения к 90°.
Пользуясь косым падением, можно наблюдать с помощью обычной дифракционной решетки дифракцию рентгеновских лучей, длина волны которых в десятки тысяч раз меньше, чем световых. Так, поставив решетку с периодом 1 мкм под углом =89°59'40", мы получим картину, соответствующую решетке с периодом около 1 Å, и можем изучить дифракцию рентгеновских лучей, длина волны которых составляет долю ангстрема *): Этот метод наблюдения дал возможность весьма точного определения длины волны рентгеновских лучей.