ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 392
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§ 95. Изображение протяженных объектов в сферическом зеркале и линзе. До сих пор мы предполагали, что источник света представляет собой светящуюся точку, находящуюся на главной оптической оси зеркала или линзы. Рассмотрим теперь изображение в сферическом зеркале или линзе небольших предметов, расположенных вблизи их главной оси. Выражение «небольшой предмет» будет означать, что данный предмет виден из центра зеркала или линзы под малым углом. Так как отдельные точки протяженного предмета лежат вне главной оптической оси, то поставленная задача сводится к построению изображения таких «внеосевых» точек. Задача эта решается без труда. Разберем ее для случая сферического зеркала.
Пусть точечный источник света находится в точке S1на некотором расстоянии от главной оси зеркала (рис. 209). Проведем через него побочную оптическую ось. По отношению к отражению в сферическом зеркале точка S1вполне равноправна с точкой S, лежащей на главной оси зеркала на том же расстоянии от его центра С. Таким образом, если мы выделим узкий пучок лучей вблизи оси S1C, то, пользуясь результатами §91, можем утверждать, что он после отражения соберется снова в одной точке S1' — изображении точки S1. Легко видеть, что любая точка дуги S1SS2 с центром в точке С изобразится точкой, лежащей на дуге S'1'S'S2' с центром также в С. Другими словами, дуга S1'S'S2' является изображением дуги S1SS2.
Мы будем предполагать, что все точки дуги S1SS2 находятся на небольшом расстоянии от главной оси. Тогда практически можно заменить дуги S1SS2 и S1'S'S2' прямолинейными отрезками, перпендикулярными к главной оси.
Итак, мы доказали, что небольшой отрезок, перпендикулярный к главной оси, изобразится после отражения в сферическом зеркале также отрезком, перпендикулярным к главной оси. Этот вывод имеет силу только при условии достаточной малости угла, под которым объект виден из центра зеркала; в противном случае заменить дугу прямолинейным отрезком нельзя. Практически нарушение этого условия приводит к тому, что изображение становится нечетким, расплывчатым по краям.
Совершенно аналогично решается задача и для тонкой линзы. И в этом случае хорошее, четкое изображение протяженных объектов получается только при условии
, что эти объекты (их крайние точки) видны из оптического центра линзы под малым углом к главной оси. При несоблюдении этого условия изображение получается более или менее расплывчатым и искаженным.
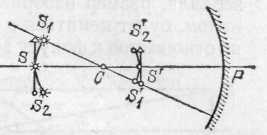
Рис. 209. Построение изображения протяженного объекта в сферическом зеркале
Изображение протяженных объектов в сферическом зеркале и линзе. До сих пор мы предполагали, что источник света представляет собой светящуюся точку, находящуюся на главной оптической оси зеркала или линзы. Рассмотрим теперь изображение в сферическом зеркале или линзе небольших предметов, расположенных вблизи их главной оси. Выражение «небольшой предмет» будет означать, что данный предмет виден из центра зеркала или линзы под малым углом. Так как отдельные точки протяженного предмета лежат вне главной оптической оси, то поставленная задача сводится к построению изображения таких «внеосевых» точек. Задача эта решается без труда. Разберем ее для случая сферического зеркала.
Пусть точечный источник света находится в точке S1на некотором расстоянии от главной оси зеркала (рис. 209). Проведем через него побочную оптическую ось. По отношению к отражению в сферическом зеркале точка S1вполне равноправна с точкой S, лежащей на главной оси зеркала на том же расстоянии от его центра С. Таким образом, если мы выделим узкий пучок лучей вблизи оси S1C, то, пользуясь результатами §91, можем утверждать, что он после отражения соберется снова в одной точке S1' — изображении точки S1. Легко видеть, что любая точка дуги S1SS2 с центром в точке С изобразится точкой, лежащей на дуге S'1'S'S2' с центром также в С. Другими словами, дуга S1'S'S2' является изображением дуги S1SS2.
Мы будем предполагать, что все точки дуги S1SS2 находятся на небольшом расстоянии от главной оси. Тогда практически можно заменить дуги S1SS2 и S1'S'S2' прямолинейными отрезками, перпендикулярными к главной оси.
Итак, мы доказали, что небольшой отрезок, перпендикулярный к главной оси, изобразится после отражения в сферическом зеркале также отрезком, перпендикулярным к главной оси. Этот вывод имеет силу только при условии достаточной малости угла, под которым объект виден из центра зеркала; в противном случае заменить дугу прямолинейным отрезком нельзя. Практически нарушение этого условия приводит к тому, что изображение становится нечетким, расплывчатым по краям.
Совершенно аналогично решается задача и для тонкой линзы. И в этом случае хорошее, четкое изображение протяженных объектов получается только при условии, что эти объекты (их крайние точки) видны из оптического центра линзы под малым углом к главной оси. При несоблюдении этого условия изображение получается более или менее расплывчатым и искаженным.

Рис. 209. Построение изображения протяженного объекта в сферическом зеркале
44. Увеличение при изображении объектов в сферических зеркалах и линзах.
Увеличение при изображении объектов в сферическом зеркале и линзе. Теперь надо рассмотреть еще вопрос о размерах изображения, получающегося в зеркале и линзе. Выполненные на рис. 210 построения сразу указывают на то, что, в отличие от случая плоского зеркала, размер изображения, даваемого сферическим зеркалом, будет меняться в зависимости от положения объекта по отношению к фокусу зеркала. Так, например, если объект
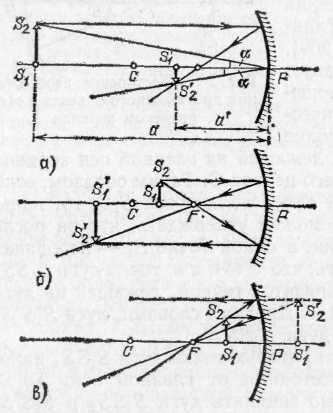
Рис. 210. Изображения протяженных объектов в вогнутом сферическом зеркале. Объект расположен: а) за центром зеркала (изображение действительное, обратное и уменьшенное); б) между центром и фокусом (изображение действительное, обратное и увеличенное); в) ближе фокуса (изображение мнимое, прямое и увеличенное)
находится много дальше фокуса вогнутого зеркала, то его изображение получается уменьшенным. Если объект находится между зеркалом и фокусом, то изображение получается мнимым и увеличенным.
Отношение линейных размеров изображения S1'S2'=у' к линейным размерам предмета S1S2=yназывается линейным, или поперечным, увеличением:
Из подобия треугольников S1PS2и S1'PS2' (рис. 210, а) находим
Легко убедиться, что равенство (96.1) справедливо и в других случаях получения изображения при помощи сферических зеркал (рис. 210, б и в).
Изображения, получаемые с помощью линзы, могут Выть также увеличенными и уменьшенными. Из подобия треугольников
S1OS2 и S1'OS2' (рис. 211) находим для
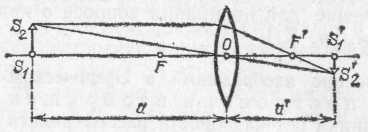
Рис. 211. Линейное увеличение линзы =S1'S2'/S1S2=a'/a
увеличения линзы точно такое же выражение, какое мы получили для сферического зеркала:
Наряду с линейным увеличением мы будем рассматривать также угловое увеличение линзы (или сферического зеркала). Угловым увеличением у называется отношение тангенсов углов ' и , составляемых лучом, выходящим из
1.
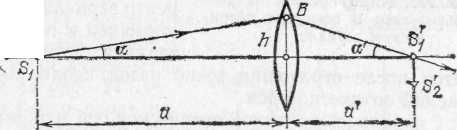
Рис. 212. Угловое увеличение линзы =tg'/tg=a/a'
линзы, и лучом, падающим на линзу, с оптической осью, т. е.
Из рис. 212 видно, что
отсюда
Сравнивая это соотношение с (96.1), находим
т.е. угловое увеличение есть величина, обратная линейному увеличению. Из этого следует, что чем больше линейное
увеличение, т. е. размеры изображения, тем меньше угловое увеличение, т. е. тем менее широки пучки световых лучей, образующих изображение. Это обстоятельство имеет важное значение для понимания вопроса о яркости изображения (см. гл. XI).
45. Проекционные оптические приборы.
Проекционные оптические приборы. Законы образования изображений в оптических системах служат основой для построения разнообразных оптических приборов. Основной частью всякого оптического прибора является некоторая оптическая система. В одних оптических приборах изображение получается на экране, который должен быть установлен в плоскости изображения, другие приборы предназначены для работы совместно с глазом. В последнем случае прибор и глаз представляют как бы единую оптическую систему и изображение получается на сетчатой оболочке глаза.
Мы будем рассматривать действие оптических приборов на основе законов геометрической оптики. Однако для решения некоторых вопросов представление о световых лучах оказывается недостаточно точным, и нам придется ссылаться на волновые свойства света, которые будут изучаться в последующих главах.
Проекционные приборы дают на экране действительное, увеличенное изображение картины или предмета. Такое изображение может рассматриваться со сравнительно большого расстояния и благодаря этому может быть видно одновременно большому числу людей.
На рис. 240 изображена схема проекционного аппарата, предназначенного для демонстрации прозрачных объектов, например рисунков и фотографических изображений на стекле (диапозитивы), фильмов и т. п. Такие аппараты называются диаскопами (диа — прозрачный). Освещение объекта 1 производится ярким источником света 2 с помощью системы линз 3, называемой конденсором. Иногда за источником устанавливается вогнутое зеркало 4, в центре которого находится источник. Это зеркало, направляя обратно в систему свет, падающий на заднюю стенку фонаря, увеличивает освещенность объекта.
Объект помещается вблизи фокальной плоскости объектива 5, который дает изображение на экране 6 (см. §97). Для резкой наводки объектив может плавно перемещаться. Проекционные системы очень часто употребляются для демонстрации рисунков, чертежей и т. п. во время лекций (проекционный фонарь). Киноаппарат представляет собой проекционную систему того же типа с тем усложнением, что демонстрируемые картины очень быстро сменяют одна другую. Фильм передвигается скачками — каждый раз на один кадр. В момент передвижения фильма световой пучок
перекрывается обтюратором. На рис. 241 представлена схема простейшего киноаппарата.
При проецировании получается обычно сильно увеличенное изображение. Так, например, при проецировании кадра кинофильма размером 18X24 мм на экран с размерами 3,6X4,8м линейное увеличение равно 200, а площадь изображения превышает площадь кадра в 40 000 раз.
Для того чтобы освещенность объекта была достаточно высокой и притом равномерной, важную роль играет правильный подбор конденсора. Казалось бы, что задачей конденсора является максимально сконцентрировать свет на изображаемом объекте. Однако это совершенно неверно. Попытки «концентрации» света на объекте приводят обычно только к тому, что конденсор дает на нем сильно уменьшенное изображение источника, и если этот последний не очень велик, то объект будет освещен крайне неравномерно. Кроме того, при этом часть светового потока пойдет мимо проекционного объектива, т. е. не будет участвовать в образовании изображения на экране. Выбор конденсора дает возможность избежать этих недостатков.