ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 379
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
При падении света на пленку или тонкую пластинку часть света
проходит сквозь нее, а часть отражается. Предположим, что монохроматический свет длины волны падает на пластинку перпендикулярно к ее поверхности. Будем рассматривать малый участок пластинки, считая его плоскопараллельным. На рис. 268 изображен ход лучей в пластин-
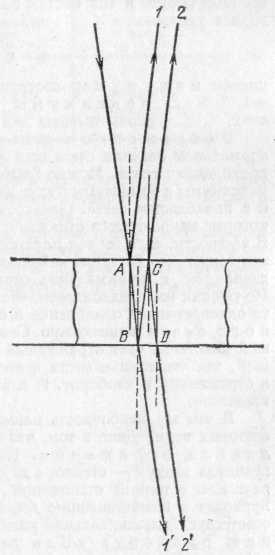
Рис. 268. Ход отраженных и проходящих лучей при двукратном отражении в пленке
ке, причем для наглядности лучи изображены не вполне перпендикулярными к ней. В отраженном свете имеем луч 1, отраженный от верхней поверхности пластинки и луч 2, отраженный от нижней поверхности. В проходящем — луч 1', прямо прошедший через пластинку и луч 2', отразившийся по одному разу от нижней и от верхней поверхностей *).
Рассмотрим сначала проходящие лучи. Лучи 1' и 2' обладают разностью хода, так как первый прошел через нашу пленку один раз, а второй — три раза. Образовавшаяся разность хода при нормальном падении света есть AB+BC+CD—АВ=ВС+CD=2h, где h— толщина пластинки. Если эта разность хода равна целому числу волн, т. е. четному числу полуволн, то лучи усиливают друг друга; если же разность хода равна нечетному числу полуволн, то лучи взаимно ослабляются. Итак, максимумы и минимумы получаются в тех местах пластинки, толщина которых hудовлетворяет условию
причем минимумы соответствуют нечетному значению n=1, 3, 5, ..., максимумы соответствуют четному значению n=2, 4, ... Таковы выводы для проходящего света.
В отраженном свете разность хода между лучами 1 и 2 при нормальном падении света есть AB+BC=2h, т. е. такая же, как и для проходящего света. Можно было бы думать, что и в отраженном свете максимумы и минимумы будут на тех же местах пластинки, что и в проходящем свете. Однако это означало бы, что места пластинки, которые меньше всего отражают света, меньше всего и пропускают его. В частности, если бы вся пластинка имела одну и ту же толщину и притом такую, что 2h равно нечетному числу полуволн, то такая пластинка давала бы и минимальное отражение и минимальное пропускание. Но так как мы предполагаем, что пластинка не поглощает света, то одновременное ослабление и отраженного, и пропущенного света невозможно.
Само собой разумеется, что в непоглощающей пластинке свет отраженный должен дополнять свет прошедший, так что темные места в проходящем свете соответствуют светлым в отраженном и наоборот. И действительно, опыт подтверждает это заключение.
В чем же ошибочность нашего расчета интерференции отраженных световых волн? Дело в том, что мы не учли различия в условиях отражения. Некоторые из отражений имеют место на границах воздух — стекло, а другие на границах стекло — воздух (если речь идет о тонкой стеклянной пластинке в воздухе). Это различие приводит к возникновению дополнительной разности фаз, которая соответствует дополнительной разности хода, равной /2.Поэтому полная разность хода для лучей, отраженных от верхней и нижней поверхностей пластинки толщиной h, равняется 2h+/2. Места минимумов соответствуют условию
где m— нечетное число; места максимумов — четным значениям m. Следовательно, максимумы и минимумы получаются в тех местах пла-
*) Как в проходящем, так и в отраженном свете имеются еще и лучи, испытавшие многократное отражение. Но они настолько слабее первых двух, что их можно не принимать в расчет.
станки, толщина которых hудовлетворяет условию
причем (m—1) обозначено через n. Минимумы соответствуют четным значениям n=0, 2, 4, ..., максимумы соответствуют нечетным значениям n=1, 3, 5, ...
Сопоставим результаты, полученные для определения положения максимумов и минимумов в проходящем и отраженном свете. Положения максимумов и минимумов соответствуют толщине пленки, определяемой из условия:
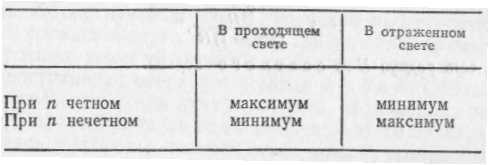
Таким образом, области максимумов в проходящем свете соответствуют областям минимумов в отраженном и наоборот — в согласии о опытом и в высказанными выше соображениями.
Применительно к кольцам Ньютона, которые обычно наблюдаются в отраженном свете (§ 126), получаем, что места максимумов соответствуют нечетным значениям n=1, 3, 5, ..., а места минимумов — четным n=0, 2, 4, ... Центральный (нулевой
n=0) минимум имеет вид темного кружка, следующее пер-
мое темное кольцо соответствует
n=2, второе n=4 и т. д. Вообще номер N темного кольца связан с числом я соотношением N=n/2.Номер N светлого кольца выражается через nформулой N=(n+1)/2.
Вместо определения толщины hтого места воздушной прослойки, которое соответствует кольцу номера N, удобнее измерять диаметр или радиус соответствующего кольца. Из рис. 269 следует: R2=(R—h)2+r2и, следовательно, толщина прослойки hсвязана с радиусом кольца rи радиусом линзы Rсоотношением
Для опытов с кольцами Ньютона пользуются линзами о очень большим радиусом R(несколько метров). Поэтому можно пренебречь величиной ft по сравнению с 2Rи упростить последнее соотношение, записав:
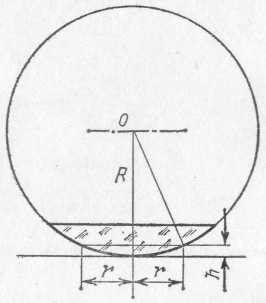
Рис. 269. К расчету радиусов колец Ньютона
Итак, для определения длины волны с помощью колец Ньютона имеем
Если измеряются радиусы темных колец, то номер кольца N=n/2. В таком случае длина волны выразится формулой
где rN есть радиус N-готемного кольца.
Проводя измерения радиусов светлых колец, мы должны иметь в виду, что N={n+1)/2.В соответствии с этим получаем соотношение
где rNесть радиус N-ro светлого кольца.
ДИФРАКЦИЯ СВЕТА
§ 128. Пучки лучей и форма волновой поверхности. Для очень большого круга вопросов, где успешно применялись построения геометрической оптики, мы характеризовали распространение света при помощи лучей. Образование параллельного пучка лучей означало, что световая энергия распространяется лишь по направлению этого пучка, не рассеиваясь в стороны, так что освещенность поверхности, на которую падает свет, остается неизменной на любом расстоянии от источника. Расходящийся пучок лучей означал распределение света по возрастающей поверхности, так что освещенность уменьшалась обратно пропорционально квадрату расстояния от точки, из которой расходятся лучи (вершина пучка). Наоборот, сходящийся пучок ;лучей означал возрастание освещенности по мере
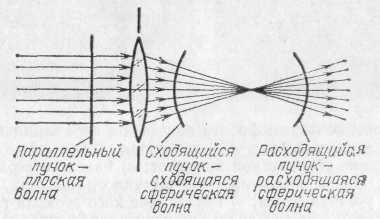
Рис. 270. Изменение формы фронта волны при прохождении через
линзу
приближения к точке схождения лучей. Роль оптических систем сводилась к преобразованию формы волновых фронтов. С точки зрения волновых представлений распространение света есть распространение волн, а роль лучей играют линии, перпендикулярные к поверхности фронта волны. Характер распространения света задается формой фронта волны (волновой поверхностью). Так, параллельный пучок лучей соответствует плоской волне, фронт которой имеет форму плоскости, перемещающейся параллельно самой себе. Сходящиеся в точке или расходящиеся из точки пучки соответствуют сферическим волновым поверхностям, центр которых лежит в точке схождения или расхождения лучей. Изменение кривизны фронта волны означает изменение угла схождения лучей.
Таким образом, прохождение волны через систему линз или зеркал сводится к изменению формы ее фронта (рис. 270).
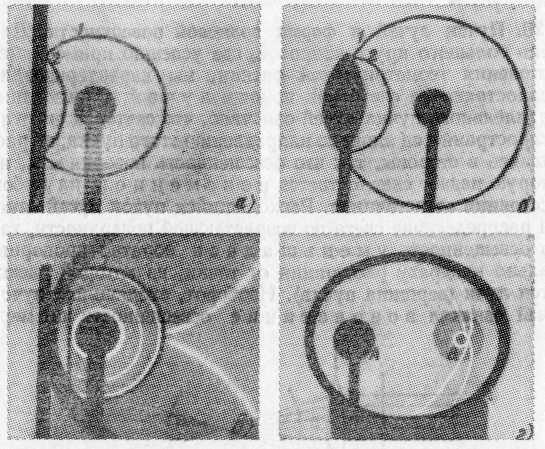
Рис. 271. Изменение формы фронта волны при отражении (фотографии звуковой волны в воздухе: 1 — падающая волна, 2 — отраженная волна). Отражение сферической волны от: а) плоского зеркала — кривизна фронта волны неизменна; б) выпуклого зеркала — кривизна фронта волны увеличивается; в) параболического зеркала (источник — в фокусе зеркала) — фронт волны становится плоским; г) эллиптического зеркала (источник — в фокусе А зеркала) — волна сходится
в фокусе В
Влияние отражения от разных поверхностей на форму фронта волны хорошо иллюстрируется на ряде снимков, приведенных на рис. 271 и изображающих отражение звукового импульса в воздухе. Аналогичные картины могут быть без труда получены и при наблюдении преломленных волн.
§ 129. Принцип Гюйгенса. Рисунки, представленные в предыдущем параграфе, дают лишь общее качественное понятие о волновом характере распространения света и о действии отражения и преломления на световую волну.
Но еще Гюйгенс сумел использовать представление о распространении волн в среде для количественного расчета законов преломления и отражения. С этой целью им был сформулирован общий принцип, которому подчиняется распространение волн. Этот принцип Гюйгенса представляют собой правило, позволяющее, исходя из положения волнового фронта в какой-нибудь момент времени, найти положение волнового фронта для ближайшего более позднего момента времени.
Согласно принципу Гюйгенса каждую точку среды, которой достигла волна, можно рассматривать как источник вторичных сферических волн, распространяющихся со скоростью, свойственной среде. Огибающая поверхность, т. е. поверхность, касающаяся всех сферических вторичных волн в том положении, которого они достигнут к моменту времени t, и представляет собой волновой фронт в этот момент.
Поверхность, на которой расположены точки среды, выбранные в качестве источников вторичных волн, является для построения Гюйгенса вспомогательной поверхностью. Она не должна обязательно совпадать с положением какого-либо волнового фронта, но может быть поверхностью, до которой первичные волны доходят в разные моменты времени.
Для отыскания же фронта волны к моменту tнадо построить положение вторичных волн к этому моменту и провести огибающую поверхность. Таким образом, из точек, достигнутых первичной волной в более ранний момент, вторичные волны успеют разойтись на большие расстояния, а из точек, позже принятых за центр вторичных волн,— на меньшие.
Принцип Гюйгенса дает возможность найти интересующую нас огибающую, выбирая вспомогательную поверхность различными способами, но окончательный результат, конечно, будет один и тот же. На рис. 272 рассматривается распространение сферической расходящейся волны, фронт которой в некоторый момент времени t0 занимает положение Р0. В разные точки вспомогательной поверхности