ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 164
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
План работы
1. Получить параметры модели множественной линейной регрессии различными способами:
а) непосредственно применяя МНК (минимизируя сумму квадратов отклонений с помощью Поиска решения);
б) решить систему уравнений МНК матричным методом;
в) найти параметры модели с помощью функции ЛИНЕЙН.
2. Записать уравнение регрессии.
3. Проверить гипотезу о равенстве нулю коэффициентов регрессии в генеральной совокупности на уровне значимости 0,05 по критерию Стьюдента.
4. Сделать вывод о статистической значимости коэффициентов регрессии.
5. Пояснить экономический смысл каждого коэффициента регрессии.
6
 . Найти доверительные интервалы для коэффициентов регрессии (доверительная вероятность 0,95).
. Найти доверительные интервалы для коэффициентов регрессии (доверительная вероятность 0,95).Исходные данные – таблица из Задания 6.
8. Тема: Сравнительный анализ факторов по степени влияния на изменение результативного признака y.
План работы.
1. Получить параметры уравнения множественной линейной регрессии и дополнительную статистику с помощью функции ЛИНЕЙН.
2. Записать уравнение регрессии.
3. Сформулировать и проверить гипотезы о равенстве нулю (о статистической незначимости) для каждого коэффициента регрессии на уровне значимости 0,05.
4. При наличии незначимых коэффициентов исключить соответствующие факторы, получить и записать новое уравнение регрессии.
5. Проверить гипотезу о несущественности уменьшения коэффициента детерминации при исключении части факторов.
6. Пояснить смысл каждого коэффициента регрессии в полученном уравнении.
7. Найти доверительные интервалы для истинных значений коэффициентов регрессии с доверительной вероятностью 0,95.
8. Рассчитать:
а) Коэффициенты средней эластичности.
б) Стандартизованные коэффициенты регрессии (бета-коэффициенты).
в) Дельта-коэффициенты.
9. Сравнив между собой рассчитанные в п. 8 коэффициенты, сделать вывод: изменение какого фактора оказывает большее влияние на изменение y.
Исходные данные – таблица из Задания 6.
9. Тема: Лаговые переменные.
План работы.
1. Представить на одной диаграмме динамику x и y (зависимость от времени).
Тип диаграммы – точечная, точки соединены отрезками.
2. Представить в виде корреляционного поля связь y(t) c x(t), связь y(t) c x(t-1), связь y(t) c x(t-2). Тип диаграммы – точечная, точки не соединены.
3. С помощью функции ЛИНЕЙН найти параметры модели
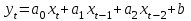
4. Проверить гипотезу о статистической значимости коэффициентов а0, а1 и а2. Уровень значимости 0,05. 5. При наличии незначимых коэффициентов исключить соответствующие факторы и заново применить функцию ЛИНЕЙН.
6. Записать полученное уравнение.
7. Применить полученное уравнение для расчета модельных значений ŷ, включая прогноз на 2023 год.
8. Представить на одном графике динамику y и ŷ (зависимость от времени).
Таблица составлена по данным Крымстат. Режим доступа http://crimea.gks.ru
Естественное движение населения
Y – Родившиеся, человек;
X – Зарегистрировано браков, единиц
| Год | t | yt | xt | xt-1 | xt-2 |
| 2014 | 1 | 24330 | 16322 | | |
| 2015 | 2 | 24039 | 17417 | 16322 | |
| 2016 | 3 | 22944 | 13493 | 17417 | 16322 |
| 2017 | 4 | 20849 | 14430 | 13493 | 17417 |
| 2018 | 5 | 20331 | 11609 | 14430 | 13493 |
| 2019 | 6 | 19214 | 13241 | 11609 | 14430 |
| 2020 | 7 | 18810 | 11149 | 13241 | 11609 |
| 2021 | 8 | 18161 | 12398 | 11149 | 13241 |
| 2022 | 9 | 16524 | 13756 | 12398 | 11149 |
| 2023 | 10 | | | 13756 | 12398 |
10. Тема: Фиктивные переменные.
План работы.
1. Представить на одном графике динамику x и y (зависимость от времени).
2. Представить в виде корреляционного поля связь y c x. Тип диаграммы – точечная, точки не соединены. Добавить к диаграмме линию тренда.
3. Найти параметры линейной модели, рассчитать значения ŷ и остатки.
4. Представить на одном графике динамику y и ŷ (зависимость от времени).
5. Представить на графике ряд остатков. Сделать вывод о наличии сезонности.
6. Добавить фиктивные переменные в количестве 11 (январь считать базовым уровнем).
7. С помощью функции ЛИНЕЙН найти параметры модели с фиктивными переменными.
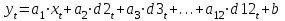
8. Проверить гипотезу о статистической значимости коэффициентов а1, а2,…, a12 на уровне значимости 0,05.
9. При наличии незначимых коэффициентов исключить соответствующие факторы, получить новое уравнение, проверить статистическую значимость коэффициентов
10. Применить полученное уравнение для расчета модельных значений ŷ.
11. Представить на одном графикt динамику y и ŷ (зависимость от времени).
Таблица составлена по данным Крымстат. Режим доступа http://crimea.gks.ru
X – Среднемесячная номинальная начисленная заработная плата работников по полному кругу организаций, рублей/
Y – Оборот розничной торговли, млн.рублей/
| Год | 2017 | 2018 | 2019 | ||||
| Месяц | x | y | x | y | x | y | |
| январь | 23599 | 16661,1 | 26345 | 17452,5 | 28117 | 19008,6 | |
| февраль | 24017 | 17075,0 | 26716 | 17561,2 | 28799 | 19046,4 | |
| март | 25125 | 18382,4 | 28645 | 19305,3 | 31263 | 20494,7 | |
| апрель | 25284 | 18470,1 | 28675 | 18932,3 | 31815 | 21312,2 | |
| май | 26323 | 19430,9 | 29257 | 20510,7 | 32625 | 22646,8 | |
| июнь | 30577 | 22134,2 | 33425 | 24321,0 | 36674 | 25349,2 | |
| июль | 26065 | 23062,2 | 28106 | 24843,9 | 31654 | 26483,3 | |
| август | 24775 | 22695,9 | 27790 | 25697,5 | 31274 | 26647,1 | |
| сентябрь | 26385 | 19359,4 | 28465 | 22593,5 | 32742 | 23595,5 | |
| октябрь | 25879 | 17217,6 | 28423 | 21743,0 | 34253 | 23463,3 | |
| ноябрь | 25795 | 16772,9 | 28400 | 20460,1 | 32565 | 22820,5 | |
| декабрь | 31975 | 18630,8 | 36027 | 22776,9 | 42505 | 23841,1 | |
11. Тема: Обоснование и моделирование линейного и полиномиального тренда.
План работы.
Ознакомьтесь с примерами обоснования выбора моделей и оценки параметров моделей,
По аналогии с примерами выполните задание согласно плану:
1. Представить данные графически. Сделать предположение о типе тренда.
Добавьте к диаграмме уравнение выбранного вами тренда и прогноз вперед на 2-3 года.
2. Выполнить идентификацию модели (определить степень полинома) по поведению приростов.
3. Найти оценку параметров модели с помощью функции ЛИНЕЙН.
4. Выполнить проверку статистической значимости коэффициента при старшей степени полинома на уровне значимости 0,05.
Сделать окончательный вывод о типе модели тренда по трем характеристикам:
а) поведение модели на периоде упреждения;
б) поведение показателей динамики (приростов);
в) статистическая значимость коэффициента при старшей степени полинома.
5. Записать уравнение модели тренда (зависимость y от t).
6. Если тренд линейный, записать экономический смысл коэффициента наклона.
Источник данных: Росстат https://rosstat.gov.ru/
Мониторинг развития информационного общества в Российской Федерации
Пример 1. Линейный тренд.
у – Число музейных предметов, внесенных в электронный каталог, тыс. единиц
| Год | y |
| 2010 | 20204,4 |
| 2011 | 23537,5 |
| 2012 | 26091,2 |
| 2013 | 30547,3 |
| 2014 | 33254,4 |
| 2015 | 35570,9 |
| 2016 | 39582,2 |
| 2017 | 42602,5 |
| 2018 | 44421,4 |
| 2019 | 46982,0 |
| 2020 | 51576,1 |
| 2021 | 55000,1 |
Пример 2. Полиномиальный тренд
Число доступных в Интернете музейных предметов, внесенных в электронный каталог и имеющих цифровые изображения на 10 000 предметов общего музейного фонда