Файл: В россии в xvixvii веках появилось намного более передовое изобретение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 279
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
или директорию диска. Каталог представляет собой список элементов, каждый из которых описывает характеристики конкретного файла, используемые дезорганизации доступа к нему — имя файла, его тип, местоположение на диске, размер. Каталогов может быть большое число, и они связываются в информационные структуры, например, в иерархическую (древовидную) систему каталогов. Каждый каталог рассматривается как файл и имеет собственное имя. Полное имя каталога или файла в такой структуре задаёт путь переходов между каталогами и файлами в логической структуре каталогов.
Структура самих файлов может быть тривиальной. Например, текст может сохраняться в виде последовательности байтов, соответствующих кодировке таблицы АSСІІ. Однако в большинстве случаев вместе c данными приходится хранить и некоторую дополнительную информацию. Для реализации контроля возможных ошибок используются так называемые самокорректирующие коды, а по каналу связи вместе с псимволами основного сообщения передаются еще к дополнительных символов, обеспечивающих избыточность кодирования и позволяющих противодействовать
помехам.
Алгебра высказываний (алгебра логики)
Учение о высказываниях — алгебра высказываний или алгебра логики является простейшей логической теорией. Она рассматривает конечные конфигурации символов и взаимоотношения между ними.
Высказывание — это всякое повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими, значениями высказываний являются "истина" и "ложь", обозначаемые 1 и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок "не", "и", "или", "если... то...", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, житейское содержание игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита:
а, b, с. Из высказываний с помощью логических связок образуются новые высказывания.
Рассмотрим наиболее употребительные логические связки.
Отрицанием высказывания х называется новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если х — истинно. Обозначается х, читается "не х" или "неверно, что х". Все логические значения высказывания х можно описать с помощью табл. 1.13. Если х — высказывание, то х — противоположное высказывание. Тогда можно образовать 0 , которое называется двойным отрицанием высказывания. Логические значения 0, очевидно, совпадают со значениями х. Эта
операция одноместная — в том смысле, что из одного данного простого высказывания
х строится новое высказывание .Х
Логическое умножение (конъюнкция). Конъюнкцией двух высказываний х и у называется новое высказывание z, которое истинно, только когда оба высказывания х и у истинны, и ложно, когда хотя бы одно из х и у ложно. Обозначается х & у или х^у,читается "х и у".
Из определения операции конъюнкции видно, что союз "и" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
Логическое сложение (дизъюнкция). Дизъюнкцией двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х и у истинно, и ложным, если они оба ложны. Обозначается х v у, читается " х или у".
Логические значения дизъюнкции описываются в табл. 1.13.
Таблица 1.13 Таблица 1.14
Импликация или логическое следование. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, когда х истинно, а у ложно, и истинным во всех остальных случаях. Обозначается х → у, читается "если х, то у" или "из
х следует у".
Высказывание х называется условием или поcылкой, высказывание у — следствием или заключением.
Из таблицы истинности видно, что если условие х — истинно, и истинна импликация х → у, то верно и заключение у.
Это классическое правило вывода постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
В случае импликации несоответствие между обычным пониманием истинности сложного высказывания и идеализированной точкой зрения алгебры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.
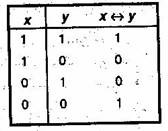
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний х и у называется новое высказывание, которое истинно, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях.
Обозначается х ↔ у, читается “для того, чтобы х, необходимо и достаточно, чтобы у" или " х тогда и только тогда, когда у". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.15.
Таблица 1.15
С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания.
Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики.
Формулы алгебры логики обозначаются большими буквами латинского алфавита А, В, С, ... Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком " ≡".
Для любых формул А, В, С справедливы следующие равносильности.
Основные равносильности:
• А ^А ≡ А
(законы идемпотентности конъюнкции и дизъюнкции);
Аv А≡ А
• А ^ 1 = А, 1 - истина;
• А^ 0 ≡ 0, 0 - ложь
• А v 1≡ 1
• А v 0 ≡А;
• А ^ А = 0 (закон противоречия);
• А v А ≡ 1 (закон исключенного третьего);
• А ≡ А (закон снятия двойного отрицания);
• А ^ (Bv А) ≡ А (первый закон поглощения);
• А v (В ^ А) ≡ А (второй закон поглощения);
• А ≡ (А ^ В) v (А ^ В) (первая формула расщепления);
• А ≡ (А v В ) ^ ( А v В) (вторая формула расщепления).
Все эти соотношения легко проверяются по таблицам истинности.
vРавносильности, выражающие одни логические операции через другие:
• Л ↔ В = (А →В )^ (В → А) ≡ ( А^В ) v (А ^ В ) ≡ (А v В ) ^ (А v В) (основная формула доказательств теорем существования);
• А→ В ≡ Аv В ≡ (А ^ В )
• А vВ ≡ А → В ≡ А^ В;
• А ^ В ≡ (А→ В )≡ АvВ;
• А ^ В ≡ А v В (первый закон де Моргана);
• А v В ≡ А ^ В (второй закон де Моргана);
• А ^ В ≡ А v В;
• А v В ≡ А ^ В.
Именно из равносильностей этой группы формул следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, держащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
Равносильности, выражающие основные законы алгебры логики:
• А ^ В ≡ В ^ А (коммутативный закон конъюнкции);
• Л v В ≡ В v А (коммутативный закон дизъюнкции);
• А ^ (В ^ С) ≡ (А ^ В ) ^ С (ассоциативность конъюнкции);
• А v(В vС) ≡ (А v В) ^ С (ассоциативность дизъюнкции);
• А^ (В v С) ≡ (А ^ В) v (А ^ С) (дистрибутивность конъюнкции относительно дизъюнкции);
• А v(В ^ С) ≡ (А v В ) ^ (А v С) (дистрибутивность дизъюнкции относительно конъюнкции). .
Формула А называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула
Структура самих файлов может быть тривиальной. Например, текст может сохраняться в виде последовательности байтов, соответствующих кодировке таблицы АSСІІ. Однако в большинстве случаев вместе c данными приходится хранить и некоторую дополнительную информацию. Для реализации контроля возможных ошибок используются так называемые самокорректирующие коды, а по каналу связи вместе с псимволами основного сообщения передаются еще к дополнительных символов, обеспечивающих избыточность кодирования и позволяющих противодействовать
помехам.
Алгебра высказываний (алгебра логики)
Учение о высказываниях — алгебра высказываний или алгебра логики является простейшей логической теорией. Она рассматривает конечные конфигурации символов и взаимоотношения между ними.
Высказывание — это всякое повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими, значениями высказываний являются "истина" и "ложь", обозначаемые 1 и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок "не", "и", "или", "если... то...", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, житейское содержание игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита:
а, b, с. Из высказываний с помощью логических связок образуются новые высказывания.
Рассмотрим наиболее употребительные логические связки.
Отрицанием высказывания х называется новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если х — истинно. Обозначается х, читается "не х" или "неверно, что х". Все логические значения высказывания х можно описать с помощью табл. 1.13. Если х — высказывание, то х — противоположное высказывание. Тогда можно образовать 0 , которое называется двойным отрицанием высказывания. Логические значения 0, очевидно, совпадают со значениями х. Этаоперация одноместная — в том смысле, что из одного данного простого высказывания
х строится новое высказывание .Х
Логическое умножение (конъюнкция). Конъюнкцией двух высказываний х и у называется новое высказывание z, которое истинно, только когда оба высказывания х и у истинны, и ложно, когда хотя бы одно из х и у ложно. Обозначается х & у или х^у,читается "х и у".
Из определения операции конъюнкции видно, что союз "и" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
Логическое сложение (дизъюнкция). Дизъюнкцией двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х и у истинно, и ложным, если они оба ложны. Обозначается х v у, читается " х или у".
Логические значения дизъюнкции описываются в табл. 1.13.
Таблица 1.13 Таблица 1.14
Импликация или логическое следование. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, когда х истинно, а у ложно, и истинным во всех остальных случаях. Обозначается х → у, читается "если х, то у" или "из
х следует у".
Высказывание х называется условием или поcылкой, высказывание у — следствием или заключением.
Из таблицы истинности видно, что если условие х — истинно, и истинна импликация х → у, то верно и заключение у.
Это классическое правило вывода постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
В случае импликации несоответствие между обычным пониманием истинности сложного высказывания и идеализированной точкой зрения алгебры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний х и у называется новое высказывание, которое истинно, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях.
Обозначается х ↔ у, читается “для того, чтобы х, необходимо и достаточно, чтобы у" или " х тогда и только тогда, когда у". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.15.
Таблица 1.15
С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания.
Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики.
Формулы алгебры логики обозначаются большими буквами латинского алфавита А, В, С, ... Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком " ≡".
Для любых формул А, В, С справедливы следующие равносильности.
Основные равносильности:
• А ^А ≡ А
(законы идемпотентности конъюнкции и дизъюнкции);
Аv А≡ А
• А ^ 1 = А, 1 - истина;
• А^ 0 ≡ 0, 0 - ложь
• А v 1≡ 1
• А v 0 ≡А;
• А ^ А = 0 (закон противоречия);
• А v А ≡ 1 (закон исключенного третьего);
• А ≡ А (закон снятия двойного отрицания);
• А ^ (Bv А) ≡ А (первый закон поглощения);
• А v (В ^ А) ≡ А (второй закон поглощения);
• А ≡ (А ^ В) v (А ^ В) (первая формула расщепления);
• А ≡ (А v В ) ^ ( А v В) (вторая формула расщепления).
Все эти соотношения легко проверяются по таблицам истинности.
vРавносильности, выражающие одни логические операции через другие:
• Л ↔ В = (А →В )^ (В → А) ≡ ( А^В ) v (А ^ В ) ≡ (А v В ) ^ (А v В) (основная формула доказательств теорем существования);
• А→ В ≡ Аv В ≡ (А ^ В )
• А vВ ≡ А → В ≡ А^ В;
• А ^ В ≡ (А→ В )≡ АvВ;
• А ^ В ≡ А v В (первый закон де Моргана);
• А v В ≡ А ^ В (второй закон де Моргана);
• А ^ В ≡ А v В;
• А v В ≡ А ^ В.
Именно из равносильностей этой группы формул следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, держащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
Равносильности, выражающие основные законы алгебры логики:
• А ^ В ≡ В ^ А (коммутативный закон конъюнкции);
• Л v В ≡ В v А (коммутативный закон дизъюнкции);
• А ^ (В ^ С) ≡ (А ^ В ) ^ С (ассоциативность конъюнкции);
• А v(В vС) ≡ (А v В) ^ С (ассоциативность дизъюнкции);
• А^ (В v С) ≡ (А ^ В) v (А ^ С) (дистрибутивность конъюнкции относительно дизъюнкции);
• А v(В ^ С) ≡ (А v В ) ^ (А v С) (дистрибутивность дизъюнкции относительно конъюнкции). .
Формула А называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула