Файл: В россии в xvixvii веках появилось намного более передовое изобретение.docx

 

 

Преобразование чисел из одной системы счисления в другую

Преобразование из десятичной в прочие системы счисления производится в с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

Рассмотрим алгоритм перевода на примере целого числа 137 в двоичную систему. Разделим его нацело на 2, получим 137:2 = 68, остаток 1. Полученный результат можно записать следующим образом:

             137 =  68 × 2¹ +1 × 2⁰.

Продолжим операцию деления дальше

 68 : 2 = 34,  остаток 0,

137  =  (34×2 + 0)× 2¹+ 1× 2⁰ = 34 × 2² + 0×2¹ + 1× 2⁰;

34 :  2  =  17, остаток 0,

137  =  (17 × 2 + 0)× 2² + 0×2¹ + 1×2⁰  =  17× 2³ + 0× 2² + 0×2¹ + 1×2⁰;

17:2 = 8, остаток 1,

137  =  (8×2 + 1) × 2³ +0×2²+0 × 2¹ + 1×2⁰  = 8×2⁴  + 1× 2³ + 

+ 0× 2² + 0× 2¹+1 × 2⁰;

                      8:2 = 4, остаток 0,

137  =  (4×2 + 0) × 2⁴+1 × 2³ + 0× 2² + 0×2¹ + 1× 2⁰ = 4×2⁵ +

+ 0 × 2⁴+ 1 × 2³+ 0 × 2² + 0 × 2¹ +1 × 2⁰;

                 4:2 = 2, остаток 0,

137  = ( 2 × 2 + 0) × 2⁵+ 0 × 2⁴ +1 × 2³+ 0 × 2²+ 0 × 2¹+ 1 × 2⁰ =

=  2 × 2⁶+ 0 ×2⁵+ 0 ×2⁴+ 1 × 2³ + 0 × 2² + 0 × 2¹ + 1× 2⁰;

                 2:2 = 1, остаток 0,

137  = ( 1 ×2 + 0) ×2⁶ + 0 × 2⁵+ 0 × 2⁴ + 1 × 2³ +  0 × 2²+ 0 × 2¹ +

+  1× 2⁰  = 1 × 2⁷ + 0 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 0 × 2¹+ 1 × 2⁰.

Далее процесс продолжать нельзя, т. к. 0 не делится нацело на 2.

 Таким образом, последовательное деление нацело на 2 позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа:  137₁₀ =10001001₂. 

Читая частное и остатки от деления в порядке, обратном получению, най­дем двоичную запись числа. Для других систем счисления все описанные действия выполняются аналогичным способом.

Например, это же число 137 в восьмеричную и шестнадцатеричную систему счисления переводится по похожим схемам.

Для дробных чисел правило последовательного деления заменяется пра­вилом последовательного умножения.

Переведем 0.2 из десятичной системы счисления   в   двоичную.   Умножим   0.2   на   2,   т.е.    0.2 × 2 = 0.4    или

0.2  = ( 0 + 0.4) × 2^-1  = 0 × 2^-1  + 0.4 × 2^-1 .

0.4 × 2  =  0.8, 0.2  = 0 × 2^-1 + (0 + 0.8) × 2^-1 × 2^-1 = 0 × 2^-1 

---

+ 0 × 2^-2 + 0.8 × 2^-2;

0.8 × 2 = 1.6,  

0.2  =  0 × 2^-1 + 0 ×2^-2  + (1 + 0.6 ) × 2^-3 = 0 × 2^-1  + 0 × 2^-2 + 1×2^-3 + 0.6 × 2^-3;

                        0.6 × 2 = 1.2,

  0.2  =  0× 2^-1 + 0 × 2^-2  +1 × 2^-3  + (1 + 0.2) × 2^-4 = 0 × 2^-1 +  0 × 2^-2  + 1 × 2^-3  + 1 × 2^-4  +0.2 × 2^-4 ;

0.2 × 2 = 0.4,  0.2  =  0 × 2^-1 + 0 × 2^-2  + 1 × 2^-3  +  1 × 2^-4  + (0 + 0.4) × 2^-5 = 0 × 2^-1  + 0 × 2^-2 + 1 × 2^-3 +1 × 2^-4 + 0 × 2^-5  + 0.4 × 2^-5 ,

т.е. 02₁₀ =0.00110011...₂. 

 Все вышеприведенные выкладки можно свести в табл. 1.3.

 

		Таблица 1.3.
	0	0.2 2
	0	0.4 2
	1	0.8  2
	1	0.6    2
	0	0.2 2
	……..	……..

Заметим, что в десятичной системе правильная дробь переводится в деся­тичную дробь в конечном виде только тогда, когда ее знаменатель имеет множители только степени двоек и пятерок, т. е. дробь имеет вид  к / (2^т 5^п ).

Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки. Таким образом, большинство деся­тичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.

Обратный перевод чисел из двоичной системы счисления в десятичную производится методом подстановки.

Для этого необходимо представить чис­ло:

137.2₁₀   =  10001001.00110011...₂ , =

=  1 × 2⁷ +1 × 2³ +1 × 2⁰  + 1 × 2^-3  +1 × 2^-4 +1 × 2^-7  +1 × 2^-8  +….. =

 ≈ 137.1992...₁₀.

Между двоичной системой счисления, восьмеричной и шестнадцатеричной существует связь, позволяющая легко переводить числа из одной системы в другую.

 Чтобы перевести число из двоичной системы счисления в восьме­ричную, надо от десятичной запятой вправо и влево выделить группы по три цифры (триады) и каждую группу независимо от других перевести в одну восьмеричную цифру.

---

 Для перевода в шестнадцатеричную систему необхо­димо выделять по четыре цифры (тетрады) и переводить каждую группу в одну шестнадцатеричную цифру.

 

Представление целых и действительных чисел в двоичном коде

Совокупность двоичных разрядов данных в ЭВМ образуют некий битовый рисунок. Группа из восьми взаимосвязанных битов называется байтом. Байт — это минимальная по размеру адресуемая часть памяти компьютера.

Существует несколько типов чисел.

 Числа могут быть положительные неотрицательные, целые точные, дробные точные, рациональные, иррацио­нальные, дробные приближенные. Оптимального представления в памяти ЭВМ для всех типов чисел создать невозможно, поэтому для каждого в от­дельности типа создается собственный способ представления.

Целые положительные числа от 0 до 255 можно представить непосредст­венно в двоичной системе счисления, при этом они будут занимать один байт в памяти компьютера (табл. 1.4).

Таблица 1.4. Представление целых положительных чисел в двоичной системе счисления

 

	Число	Двоичный код
	0	0000 0000
	1	0000 0001
	2	00000010
	3	0000 0011
	……	………
	255	11111111

 

Знак отрицательного числа кодируется обычно старшим битом, нуль ин­терпретируется как плюс, единица как минус.

Поскольку один бит будет занят, то одним байтом могут быть закодированы целые числа в, интервале от -127 до +127. Такой способ представления целых чисел называется прямым кодом.

Существует способ кодирования отрицательных целых чисел в обратном коде.

В этом случае положительные числа совпадают с положительными числами в прямом коде, а отрицательные получаются в результате вычитания из двоичного числа 1 0000 0000 соответствующего положительного числа, например, число  -7  получит код 1111 1000. Целые числа больших диапазонов представляются в двухбайтовых и четырехбай­товых адресах памяти.

---

Точность представления действительных чисел в памяти ЭВМ ограниче­на. Для представления действительных чисел используется форма их записи, называемая формой с плавающей точкой:

Х = т – g^p,^:

где:  т— мантисса числа,  g — основание системы счисления, р— целое число, называемое порядком.

При этом для десятичной системы счисления , мантисса выбирается в диапазоне 1 /g ≤ │m │ < g , т. е. 0.1≤│m│ < 1. Такая форма

представления называется нормализованной.

Существует несколько международных стандартов представления дейст­вительных чисел в памяти компьютера. Рассмотрим четырехбайтовый стан­дарт (рис.1.).

Здесь зафиксированы три группы разрядов. Первый разряд хранит знак мантиссы. За ним следуют разряды, определяющие порядок. С первого по двадцать третий разряд располагается сама мантисса числа. Вместо истинного порядка хранится число, называемое характеристикой (или смещенным порядком). Характеристика равна порядку со смещением, причем смещение используется для более удобного хранения положительных и отрицательных действительных чисел.   

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диа­пазон представления чисел в компьютере при заданном формате.

 

 

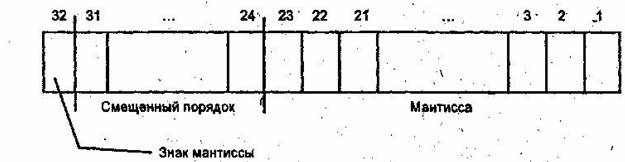
Рис. 1. Четырехбайтовое представление действительного числа

Для представления основных видов информации (числа, символы, графи­ка, звук) в системах программирования используются специального вида аб­стракции — типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных.

Кодирование текстовых и символьных данных

В двоичной системе счисления кодирование "внешних" символов основывается на сопоставлении каждому из них определенной группы двоичных знаков. Двоичное кодирование символьных данных производится заданием кодовых таблиц, в которых каждому символу ставится в соответствие одно- или двухбайтовый код. Восьми двоичных разрядов достаточно для кодирования 256 различных cимволов. Этого количества достаточно, чтобы выразить все символы английского и русского алфавита, а также знаки препинания, символы основных арифметических операций и некоторые специальные символы.

---

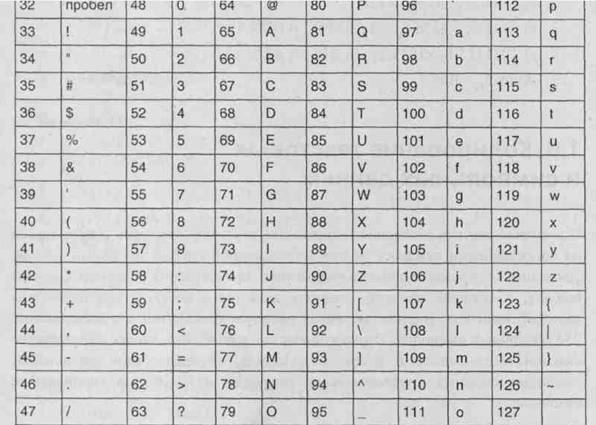
Наиболее популярная таблица АSСІІ (американский стандартный код информационного обмена) разработана институтом стандартизации США) в 1981 году (табл. 1.10).

Коды с 0 до 127 составляют базовую (основную) таблицу, коды со 128 по 255 — расширенную (дополнительную) таблицу. Дополнительная таблица отдана национальным алфавитам и символам псевдографики.

Аналогичные системы кодирования текстовых данных были разработаны и в других странах. Так, в СССР действовала система кодирования КОИ-8 (код информационного обмена восьмизначный). Компанией Microsoft была введена кодировка символов русского языка, известная как кодировка  Windows1251.

Во многих азиатских странах 256 кодов не хватило.

В 1991 году произво­дители программных продуктов (Microsoft , IВМ, Арр1е) выработали единый стандарт Unicode 3.0.

 Этот код построен по 31-битной схеме. Все текстовые документы в этой кодировке вдвое длиннее, зато она содержит буквы латин­ского и многих национальных алфавитов, спецсимволы и т. п.

 

                             Таблица 1.10. Базовая таблица кодировки АSСІІ

 

Кодирование графических данных

Различают три вида компьютерной графики: растровую, векторную и фрак­тальную.

Они отличаются принципами формирования изображения при ото­бражении на экране монитора или при печати на бумаге.

Если графические объекты формируются в виде множества точек (пиксе­лов) разных цветов и разных яркостей, то это называется растровой графи­кой. В Интернете применяются только растровые иллюстрации. Основным элементом растрового изображения является точка. Если изображение экран­ное, то эта точка называется пикселом. В зависимости от того, на какое гра­фическое разрешение экрана настроена операционная система компьютера, на экране могут размещаться изображения 640x480, 800x600, 1024x768 и бо­лее пикселов.

При кодировании растровых изображений в памяти компьюте­ра должна храниться информация о каждом пикселе. С размером изображе­ния непосредственно связано его разрешение. Этот параметр измеряется в dpi      ( точек на дюйм).

В растровой графике общепринятым на сегодняшний день считается пред­ставление черно-белых иллюстраций в виде комбинации точек с 256 града­циями серого цвета. Эти мельчайшие точки образуют характерный узор, называемый 

---