Базис	Свободный член, bi	Переменные							Оценочные отношения
		x1	x2	x3	x4	x5	x6
x3	18	1	3	1	0	0	0	18/3=6
x4	16	2	1	0	1	0	0	16/1=16
x5	5	0	1	0	0	1	0	5/1=5		q=3
x6	21	3	0	0	0	0	1	21/0=∞
F	0	-2	-3	0	0	0	0
			s=2

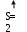Наименьшим числом среди оценочных отношений является 5, поэтому третья строка будет разрешающей. Выделим её в таблице и запомним её номер полагая q=3. На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент а₃₂=1.

Строим таблицу 2.3 следующим образом:

Таблица 2.3 - Второй шаг

Базис	Свободный член, bi	Переменные						Оценочные отношения
		x1	x2	x3	x4	x5	x6
x3	3	1	0	1	0	-3	0	3	q=1
x4	11	2	0	0	1	-1	0	5,5
x2	5	0	1	0	0	1	0	∞
x6	21	3	0	0	0	0	1	7
F	15	-2	0	0	0	3	0
		s=1

---

а) в первом столбце базисную переменную x₅, находящуюся в разрешающей строке, заменим переменной x₂, расположенной в разрешающем столбце;

б) расставляем нули и единицы в столбцах, которые соответствуют базисным переменным: ставим единицу, если клетка на пересечении столбца и строки с базисными переменными с одинаковым индексоми ноль - если с разными индексами.

Элементы строки с номером q=3 получаем делением каждого элемента разрешающей строки таблицы 1 на разрешающий элемент а₃₂=1;

Остальные клетк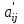и и 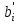заполняем по правилу прямоугольника. Вершины прямоугольника выбираем следующим образом (рис. 2.9):



Рис. 2.9. Правило прямоугольника

- одна из вершин - клетка (i,j),

- по диагонали с ней расположена клетка с разрешающим элементом (q,s);

- третья клетка находится на пересечении строки i и разрешающего столбца, т. е. клетка (i,s);

- четвёртая клетка находится на пересечении столбца j и разрешающей строки, т.е. клетка (q,j).

;

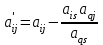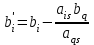
В итоге получим таблицу 2.3.

Критерий оптимальности в таблице 2.3 не выполнен. Разрешающим будет столбец 1, а разрешающей строкой - строка 1. Разрешающий элемент . Построим новую таблицу 2.4.

Таблица 2.4 - Третий шаг

Базис	Свободный член, bi	Переменные								Оценочные отношения
		x1	x2	x3	x4	x5		x6
x1	3	1	0	1	0	-3		0		∞
x4	5	0	0	-2	1	5		0		1	q=2
x2	5	0	1	0	0	1		0		5
x6	12	0	0	-3	0	9		1		1,333
F	21	0	0	2	0	-3		0
							s=5

1   2   3   4   5   6   7   8

---

Критерий оптимальности в таблице 3 не выполнен. Разрешающим будет столбец 5, а разрешающей строкой - строка 2. Разрешающий элемент 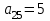. Построим новую таблицу 2.5.
Таблица 2.5 - Четвертый шаг

Базис	Свободный член, bi	Переменные							Оценочные отношения
		x1	x2	x3	x4	x5	x6
x1	6	1	0	-0,2	0,6	0	0
x5	1	0	0	-0,4	0,2	1	0
x2	4	0	1	0,4	-0,2	0	0
x6	3	0	0	0,6	-1,8	0	1
F	24	0	0	0,8	0,6	0	0

Критерий оптимальности в таблице 4 выполнен. Целевая функция F_max=24 достигается при X=(6;4;0;0;1;3).

Оптимальное решение задачи линейного программирования можно "считать" из симплекс-таблицы следующим образом. Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения — в столбце " Свободный член,

---

b_i ". В данном примере имеем следующее:

1. 
   ежедневно следует производить 6 ед. краски х1;
   
2. 
   ежедневно следует производить 4 ед. краски х2;
   
3. 
   ежедневный доход составляет 24 у.е.
   

С помощью симплекс-таблицы можно получить много дополнительной информации (кроме непосредственно оптимального решения).

1. Состояние ресурсов.

2. Цена единицы ресурсов (двойственные цены).

3. Все данные, необходимые для проведения анализа чувствительности оптимального решения.

Покажем, как определить состояние (статус) ресурсов. Статус ресурса определяется как дефицитный или недефицитный, в зависимости от того, будет он использован полностью или нет. Эту информацию можно получить из результирующей симплекс-таблицы путем проверки значений дополнительных (остаточных) переменных, ассоциируемых с соответствующими ограничениями, накладываемыми на ресурсы.

Если дополнительная переменная равна нулю, значит, ресурс использован полностью, и он получает статус дефицитного.

Положительное значение дополнительной переменной указывает на недефицитность соответствующего ресурса. В нашем случае мы имеем дефицит сырья М1 и М2, т.к оно используется полностью при х1=6 и х2=4.

Переменные х5=1 ед. и х6=3 ед. говорят о том, что при наличии достаточного сырья из-за неполного удовлетворения потребностей изданий, можно было бы увеличить выпуск краски х1 на 1 ед., а краски х2 – на 3 ед.

Решение задач линейногопрограммирования с использованием MS EXCEL

Общий алгоритм решения

Как отмечалось выше, в качестве инструмента решения оптимизационных задач используется математическое программирование.

Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.

В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функция F(х₁, х₂, ..., х_n) при условиях а_i(х₁, x₂, ..., х_n) ≤b_i, (і= 1 ^{̅̅̅ ̅ ̅̅}m), г

---

де F и a_i заданные функции, а b_i – некоторые действительные числа.

В зависимости от свойств функций F и a_i математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.

Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции F и а_i, линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.

Для решения задач оптимизации в MS Excel 2010 используется инструмент «Поиск решения».

Общий алгоритм решения оптимизационных задач в MS Excel 2010 следующий:

1. 
   Составить математическую модель.
   
2. 
   Ввести на рабочий лист Excel условия задачи:
   

а) создать таблицу на рабочем листе для ввода условий задачи;

б) ввести исходные данные, целевую функцию, ограничения и граничные условия.

3. 
   Выполнить команду «Данные – Анализ - Поиск решения».
   
4. 
   Указать параметры в диалоговом окне «Параметры поиска решения», выполнить решение.
   
5. 
   Проанализировать полученные результаты.
   

Настройка доступа к инструменту Поиск решения

Доступ к инструменту Поиск решения осуществляется с помощью команды Данные Анализ Поиск решения (рис. 2.10).



Рис. 2.10. Режим «Поиск решения»

Если команда «Поиск решения» или группа «Анализ» отсутствует на вкладке «Данные», то необходимо загрузить соответствующую надстройку:

1. 
   Выбрать команду «Файл – Параметры».
   
2. 
   В диалоговом окне «Параметры» Ехсеl выбрать категорию «Надстройки»(рис. 2.12).
   

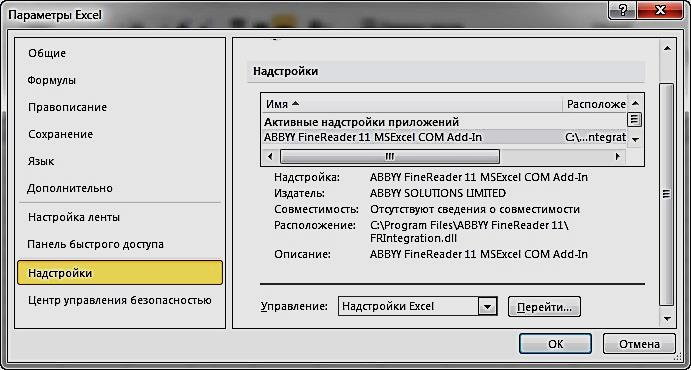
Рис. 2.12. Окно «Параметры»

---

Смотрите также файлы

• 3 Социальнопсихологический тренинг общения.doc

• Приоритетные направления начального общего образования в рамках реализации Федерального государственного образовательного стандарта второго поколения.doc

• Едеральное агентство по техническому регулированию и метрологии н ациональный.doc

• Практическая работа Использование библиотеки цифрового образовательного контента в учебной деятельности.docx

• Минобрнауки россии санктПетербургский государственный.docx