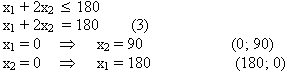
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют данным ограничениям (на рисунке они указаны стрелками). Заштрихованная область ОАВСD - область допустимых решений функции F.

Построение прямой уровня.

Возьмем произвольную точку, принадлежащую области допустимых решений - ОАВСD, например, точку М с координатами (20; 20).

F(20; 20)=20+2*20=60

Прямая уровня будет иметь следующий вид: x₁+2x₂=60

Найдем две точки этой прямой - (20; 20) и (60; 0) (если x₂=0, то x₁=60). Построим прямую уровня. Вектор а {1; 2}, отложенный от точки М указывает направления возрастания функции F. Максимизируем данную функцию F (Рис. 2.8).



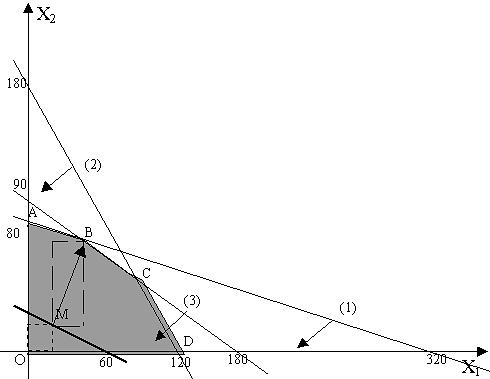
Рис. 2.8. Пример 6

Максимизация целевой функции F.

Так как построенный вектор a - является вектором, указывающем направление возрастания функции F, то передвижение прямой уровня в направлении вектора a позволит нам найти точку максимума. В нашем случае - это точка В. Данная точка расположена на пересечении двух прямых (1) и (3), поэтому, чтобы найти ее координаты необходимо решить следующую систему уравнений:



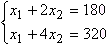
Вычтем из второго уравнения первое.

Получается 2x₂=140 или x₂ =70 . Подставим найденное значение x₂ в первое уравнение: x₁=180 - 140=40

(40; 70) - точка, соответствующая оптимальному решению задачи, следовательно, максимальная прибыль составляет 40+2*70=180. Значит, чтобы получить максимальную прибыль, фирме необходимо выпускать сорок единиц продукции вида А и семьдесят единиц продукции вида В.

Ответ: Для получения максимальной прибыли необходимо выпускать 40 единиц продукции вида А и 70 единиц продукции вида В.

Решение задач линейного программирования симплексным методом

Графический метод позволяет наглядно представить процедуру поиска оптимального решения задачи линейного программирования, но, в силу ограниченности размерности задачи, играет лишь иллюстративную роль.

Симплексный метод – универсальный метод, позволяющий найти решение любой задачи линейного программирования (ЗЛП), если, разумеется, задача разрешима. Этот метод осуществляет

---

направленный перебор вершин допустимого множества (опорных планов ЗЛП), то есть позволяет из начальной вершины за кратчайшее число шагов перейти в точку оптимума.

Применяют симплекс-метод к задаче канонического (стандартного) вида, в которой все ограничения – равенства с неотрицательной правой частью и на все переменные накладывается условие неотрицательности.

Для перехода от ограничений задачи, представленных в виде неравенств, к ограничениям-равенствам в левую часть неравенства вводятся неотрицательные дополнительные переменные с коэффициентами (+1), если неравенство имеет вид « ≤ », и с коэффициентами (-1) в случае неравенства вида « ≥ ». В целевую функцию дополнительные переменные входят с коэффициентом 0.

Алгоритм симплекс-метода

Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений. Алгоритм симплекс-метода всегда начинается с некоторого допустимого базисного решения и затем пытается найти другое допустимое базисное решение, "улучшающее" значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в небазисные. Это необходимо, чтобы новое решение содержало в точности m базисных переменных. В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная — исключаемой (из базиса).

Два правила выбора вводимых и исключающих переменных в симплекс-методе назовем условием оптимальности и условием допустимости. Сформулируем эти правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода.

Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в F-строке. Если в F-строке есть несколько таких коэффициентов, то выбор вводимой переменной делается произвольно. Оптимальное решение достигнуто тогда, когда в F-строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными).

---

Условие допустимости. Как в задаче максимизации, так и в задаче минимизации в качестве исключаемой выбирается базисная переменная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.

Последовательность действий, выполняемых в симплекс-методе.

Шаг 1. Находится начальное допустимое базисное решение.

Шаг 2. На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются.

Шаг 3. На основе условия допустимости выбирается исключаемая переменная.

Шаг 4. Методом Гаусса-Жордана вычисляется новое базисное решение. Переход к шагу 2.

Вычисления в симплекс-методе выполняются итерационно в том смысле, что условия оптимальности и допустимости, а также вычисления применяются к текущей симплекс-таблице, в результате чего получается следующая таблица. Мы будем называть последовательные симплекс-таблицы итерациями. (Симплекс-метод с ограничениями «≥» рассмотрен в приложении 1).

Пример 7.

Предприятие выпускает два вида краски (х1 и х2) для полиграфических изданий из двух материалов (М1 и М2). Для выпуска краски х1 нормы расхода материалов составляют 1 ед. для М1 и 3 ед. для М2, для краски х2, соответственно: М1 – 2 ед., М2 – 1 ед. Запасы сырья составляют: М1 – 18 ед. и М2 – 16 ед. Краску х1 использует одна группа полиграфических изданий в пределах не более 5 ед., а краску х2 – три издания в пределах не более 21 ед.. Отпускная цена краски составляет: х1 – 2 у.е., х2 – 3 у.е. Определить оптимальный план производства для достижения максимальной прибыли при условии использования сырья в пределах запасов.

Решить задачу с помощью симплексных таблиц:

Математическая модель задачи следующая:



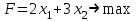
При ограничениях:



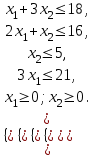
Таким образом, для получения начального опорного решения, во-первых, приведем задачу к каноническому виду путем введения в левую часть ограничений дополнительных переменных. при этом все переменные распадаются на две группы: m дополнительных и (n – m) – основных. во-вторых,

---

основные переменные приравняем нулю, тогда m дополнительных переменных (являющихся базисными) примут значения, равные правым частям ограничений.

Расширенная система имеет вид:



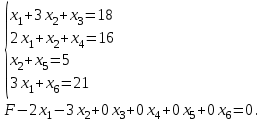
Здесь х3, х4, х5, х6 — дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства (если неравенство типа «≥», то дополнительная переменная добавляется со знаком «-».

При х1 и х2 равными 0, получаем: х3=18, х4=16, х5=5, х6=21.

Заполним первую симплексную таблицу 2.1:

Таблица 2.1 – Опорный план

Базис	Свободный член, bi	Переменные						Оценочные отношения (bi / аis)
		x1	x2	x3	x4	x5	x6
x3	18	1	3	1	0	0	0
x4	16	2	1	0	1	0	0
x5	5	0	1	0	0	1	0
x6	21	3	0	0	0	0	1
F	0	-2	-3	0	0	0	0

---

Элементы целевой строки таблицы не соответствуют условию оптимальности, так как среди них имеются отрицательные величины. Это свидетельствует о возможности увеличения целевой функции, следовательно, опорное решение, не является оптимальным.

То обстоятельство, что базисными сейчас являются дополнительные переменные, означает, что никакая проду/кция не производится и все имеющиеся ресурсы не используются.

Переход к новому опорному плану

Поскольку проверяемое решение не является оптимальным, найдем другое опорное решение, «улучшающее» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо свободной (нулевой) переменной (х1 или х2) ведет к улучшению значения целевой функции. Но для того, чтобы свободная переменная стала положительной (перешла в число базисных переменных), надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в разряд свободных. Это необходимо, чтобы новое решение содержало в точности m базисных переменных.

Таким образом, переход к новому опорному плану осуществляется путем замены базисных переменных. При этом выбранная для ввода в число базисных свободная переменная называется вводимой, а удаляемая в разряд свободных базисная переменная – выводимой.

Выбор вводимой в число базисных переменной определяется условием оптимальности F≥0: вводимая в число базисных переменная определяется максимальной по абсолютной величине отрицательной оценкой при решении задачи на максимум целевой функции и наибольшей положительной оценкой – при решении задачи на минимум. Соответствующий столбец коэффициентов в симплекс-таблице будем называть ключевым (S). В нашем случае это столбец х2, в котором F=-3.

Для определения ключевой строки (q), рассчитаем оценочные отношения (табл. 2.2). Из полученных значений следует выбрать минимальное. Такое значение определится из следующего соотношения:

.

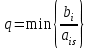Таблица 2.2 – Первый шаг. Определение ключевого элемента

---

Смотрите также файлы

• 3 Социальнопсихологический тренинг общения.doc

• Приоритетные направления начального общего образования в рамках реализации Федерального государственного образовательного стандарта второго поколения.doc

• Едеральное агентство по техническому регулированию и метрологии н ациональный.doc

• Практическая работа Использование библиотеки цифрового образовательного контента в учебной деятельности.docx

• Минобрнауки россии санктПетербургский государственный.docx