Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл (2,25Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 135

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

24
R₀_R_i

i1

_hf x_i

i1

24 ^^f

xdx. (3.12)

К интегралу в формуле (3.12) мы перешли, «используя» метод средних

^{прямоугольников}^для^{функции}f^x^.

Формула (3.12) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, данная оценка является априорной, так как не требует знания значения вычисляемого интеграла. Степень, в которую возводится шаг h , называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок точности. Аналогично можно получить априорные оценки погрешностей других рассмотренных ранее методов.

Оценим погрешность метода левых прямоугольников. Погрешность

^инте^г^р^и^р^о^в^а^н^и^яR_i^н^а^отре^з^кеx_i_₁, x_i ^равняе^т^ся^ра^з^нос^т^и^ме^ж^ду^точ^н^ым

^{значением}^{интеграла}^и^его^{приближенным}^{значением}hfx_i_₁^:

R_i

x_i

_f

^xi1

xdx hf

_h2

  
^xi1 ₂

f^x_i_₁.

Из полученного выражения видно, что основной член погрешности на каждом частичном отрезке имеет второй порядок. Поскольку полное число отрезков интегрирования равно n , то полная погрешность метода левых прямоугольников может быть рассчитана следующим образом:

_n __hn

^   ^hb

^ 

2
R₀_R_i

i1

_hf

i1

^xi1

_f xdx.

a

2
Результат оценки погрешности формулы правых прямоугольников будет таким же.

Погрешность формулы трапеций оценивается аналогичным образом.

Так как значение интеграла на отрезке x_i_₁, x_i вычисляется по формуле

^h fx 

fx

^, то погрешность может быть рассчитана по формуле:

₂i i1
R_i
x_i

_f

^xi1
xdx

 ^h

2
^fi1 ^

   ^h3

f_i
12
^x_i.

f
Следовательно, полная погрешность формулы трапеций на отрезке

a,b может быть рассчитана следующим образом:

 n   ^h2 n

^    ^h2 b

a

^ 

12
R₀_R_i

i1

_hf x_i

i1

12 ^^f

xdx

Далее приведены окончательные результаты оценки погрешностей:

Методы левых и правых прямоугольников

₂_f



b

0
R ^h^xdx.

a

Метод средних прямоугольников

Метод трапеций

_h²b

24 ^^f


R₀

a

a
  ^h2 b

^xdx.
^ 

R₀

Метод Симпсона

12 ^^f

xdx.

  ^h4 b

IV __

a
^R⁰180 ^^f

xdx.

Методы левых и правых прямоугольников являются методами первого порядка точности. Методы средних прямоугольников и трапеций имеют второй порядок точности, при этом метод трапеций обладает вдвое большей по абсолютной величине погрешностью. Поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности. Метод Симпсона имеет четвертый порядок точности с очень малым числовым коэффициентом. Формула Симпсона позволяет получить очень высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае, методы второго порядка точности могут дать большую точность, чем метод Симпсона.

1 ... 7 8 9 10 11 12 13 14 15

Вычисление интегралов с заданной точностью

Используя приведенные в разделе 3.3 оценки погрешности вычисления интегралов, можно априори определить шаг интегрирования h , при котором погрешность вычисленного результата гарантированно не превысит некоторую заданную погрешность  . Однако на практике пользоваться априорными оценками погрешности не всегда удобно. В таких случаях контроль точности получаемого результата можно организовать следующим

образом. Пусть вычисления проводились с постоянным шагом hи

_Ih _–

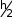вычисленное с шагом hприближенное значение интеграла I. Если затем

вычислить приближенное значение

_I^h₂

с шагом

, то в качестве оценки

погрешности последнего вычисленного значения можно рассматривать

величину

I^h ²^ I

 I^h ²^ I^^h^.

При необходимости вычислить результат с заданной точностью 

расчеты повторяют с последовательно уменьшающимся (обычно вдвое)

шагом hдо тех пор, пока не выполнится условие Можно применить указанное правило для

I^h ²^ I^^h^

контроля

  . погрешности на

^ка^ж^дом^час^т^и^чн^ом^от^р^езкеx_i_₁, x_i^,

i 1, n. При этом длина очередного шага

h_i x_i x_i_₁, посредством последовательного уменьшения начальной длины

вдвое, устанавливается такой, чтобы выполнялось неравенство

I^h ²^ I^^h^  ^hⁱ
. (3.13)

ⁱⁱ b a

Тогда, в худшем случае, ошибка вычисления значения интеграла на всем отрезке интегрирования не будет превосходить сумму локальных погрешностей

n

_h_i

_i1 ___,

b a

то есть не будет превосходить заданного уровня погрешности.

Способ вычисления интеграла с автоматическим выбором шага имеет то преимущество, что он «приспосабливается» к особенностям подынтегральной функции: в областях резкого изменения функции шаг уменьшается, а там, где функция меняется слабо, – увеличивается. Такого рода алгоритмы называются адаптивными, то есть приспосабливающимися. Их использование позволяет сократить затраты вычислительных ресурсов

без потери точности вычисления.

Одним из подходов к экономии вычислительных ресурсов ЭВМ при

Смотрите также файлы

Конкурса Семейная память.docx

Урок Формирование единых государств в Европе и России.docx

Логическое моделирование основано На основе десятичных логарифмов.docx

Анализ ассортимента детского питания в аптеке.docx

Самые большие современные птицы.docx

Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Вычисление интегралов с заданной точностью

Смотрите также файлы

Информация

Списки файлов

Дополнительно