Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 138
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



















-
Объем тела вращения
Если криволинейная трапеция, ограниченная кривой
y f(x) и
прямыми ???? = 0, ???? = a, ???? = b, вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
b
Vx y2dx
a
Если же криволинейная трапеция, ограниченная кривой
x ( y) и
прямыми ???? = 0, ???? = c , ???? = ????, вращается вокруг оси Oy, то объем тела вращения вычисляется по формуле
d
Vy x2dy
c
Пример 8. Найти объем тела, образованного вращением вокруг оси Ох
фигуры, расположенной в первой четверти и ограниченной параболой
y 2x2 , прямой y 3x 5 и осью Ох.
Найдем точки пересечения линий:
2x2 3x 5 ,
откуда
x 5 , x1.
 1 2 2
1 2 2Вычислим значения ординаты при
x2 1. Получаем
y2 2.
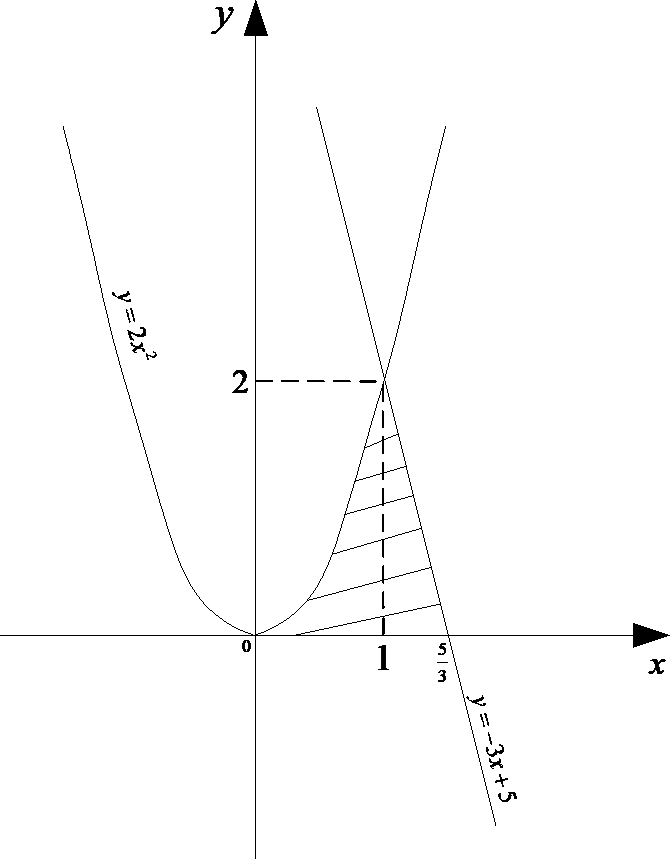 Разобьем полученную фигуру на две с помощью прямой
Разобьем полученную фигуру на две с помощью прямойx1.
Искомый объем будет складываться из двух объемов.
5 5
1 2 3 2 1 3
V 2x2 dx 3x 5 dx 4 x4dx 9x2 30x 25dx
0 1 0 1
x5 1 5 4 125 25 5




 4 3x3 15x2 25x3
4 3x3 15x2 25x3 15 25 3 15 25
5 0
1 5
9 9 3
4
25 5 15 15 13 4
8
76 .
5 9 9 9 5 9 45
Пример 9. Найти объем тела, образованного вращением вокруг оси Ох фигу-
 ры, ограниченной кривой у и прямой 2 y-x 1.
ры, ограниченной кривой у и прямой 2 y-x 1.Найдем точки пересечения линий у
и

 x1 ,
x1 ,2
y x 1 :
 2
24(x1) (x1)2 ,
откуда
x1 1,
x2 3 .
Вычислим значения ординат: при
x1 1 получаем
y1 0 , при
x2 3
получаем
y2 2.
 2,5
2,52
1,5
1
-2 -1
0,5
0
-0,5 0 1 2 3 4 5
-1
-1,5
Искомый объем будет вычисляться как разность двух объемов:
3 2
3 1 1 2 3
3 2
 V x1 dx x dx x1dx
V x1 dx x dx x1dx x1
dx
1 1 2 2
1 4 1
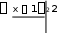
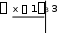 3 3
3 3
16 8

4
1
8 .

 3 3
3 31
Для решения подобных задач в Maxima следует выполнить следующиедействия:
-
Построить криволинейную трапецию. -
Найти точки пересечения кривых. -
Составить и вычислить определенный интеграл с помощью программы Maxima и вручную. -
Записать ответ.
Пример 10. Найти объем тела, образованного вращением фигуры,
ограниченной линиями
Oy.
y 1
x2 1
, ???? = 0, ???? = 0, ???? = 1 вокруг оси а) Ox, б)
Построим график функций
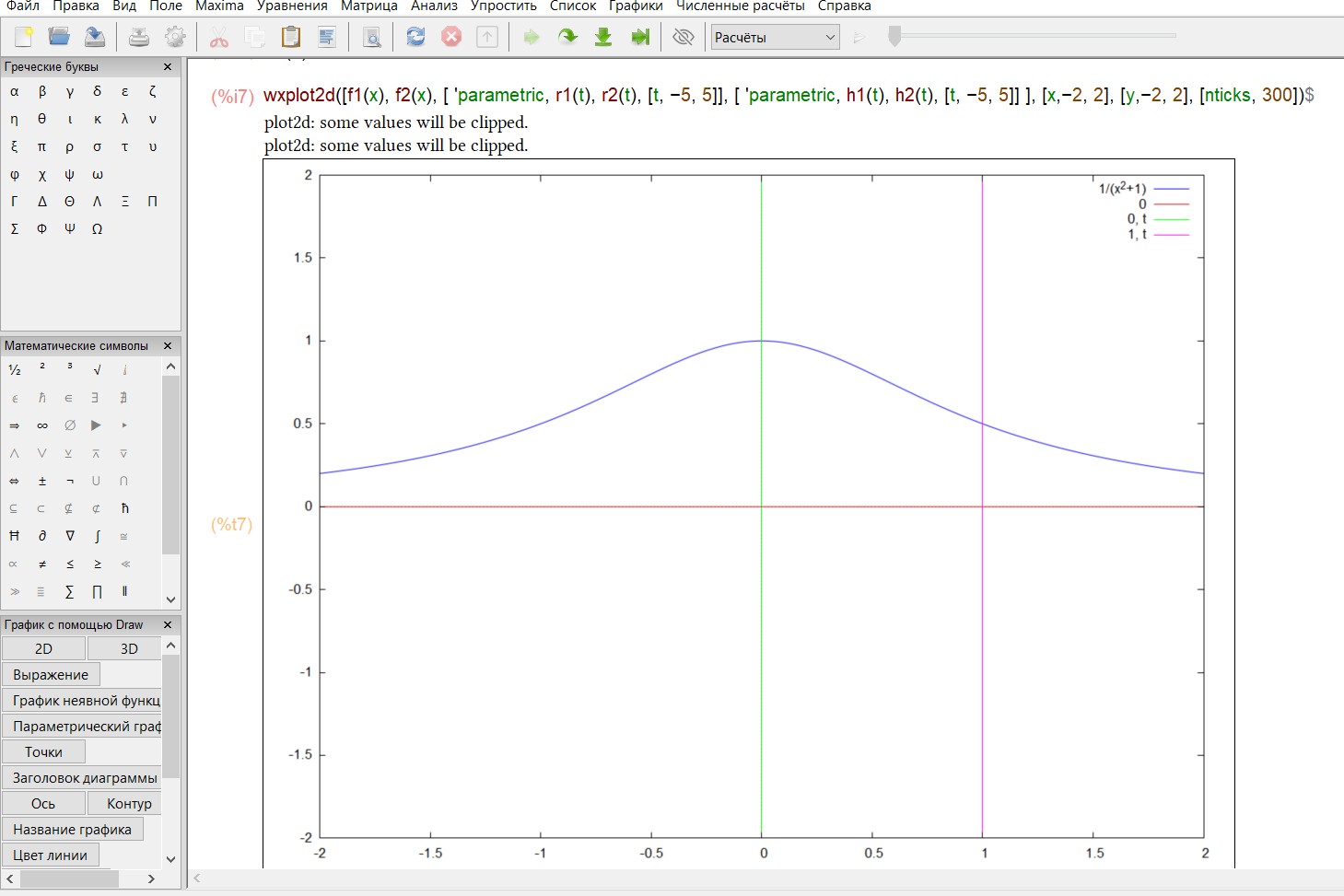
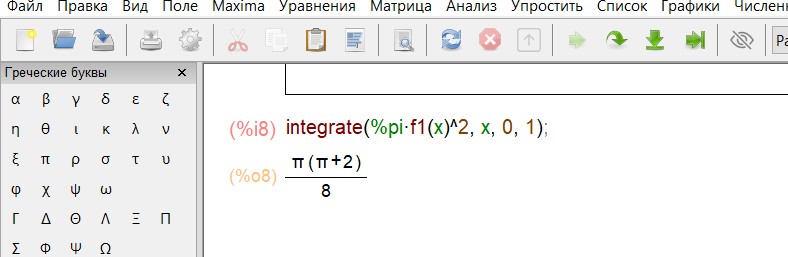
а) Если трапеция вращается вокруг оси Ox,тогда вычисляем интеграл:
б) Если трапеция вращается вокруг оси Oy,тогда область нужно разделить на две подобласти:
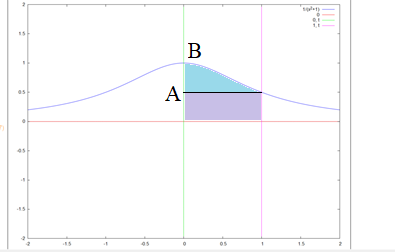

 Найдем ординаты точек Aи Bи вычислим объем тела вращения:
Найдем ординаты точек Aи Bи вычислим объем тела вращения: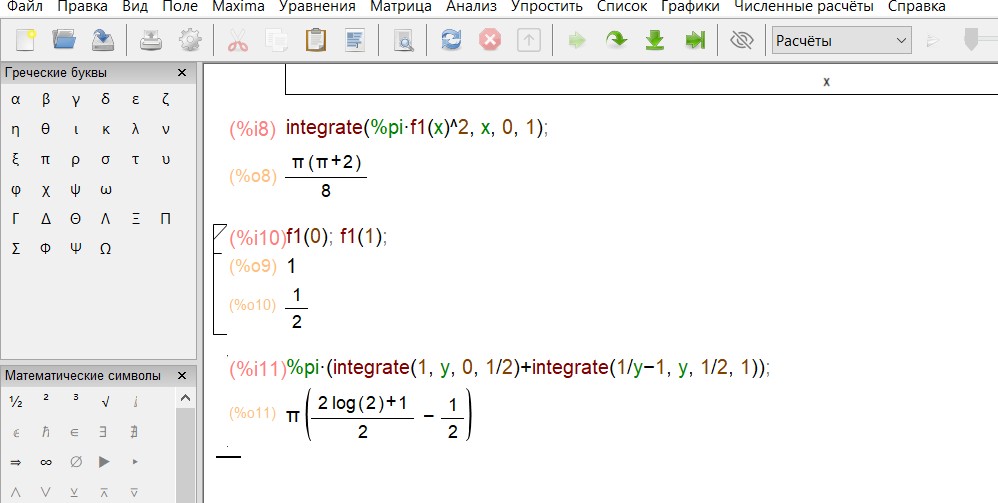
Задача 4. Вычислить объем тела