Данный инструмент позволяет построить окружность по двум точкам. Необходимо выбрать первую точку, которая будет центром, и точку на окружности.

2. Окружность по центру и радиусу.

Этот инструмент строит окружность по центру, для этого необходимо указать точку, и введённому с клавиатуры радиусу.

3. Циркуль.

Выбрав этот инструмент, вам необходимо будет указать отрезок (или 2 точки), который будет радиусом новой окружности и выбрать центр.

4. Окружность по трём точкам.

Укажите три точки на графическом представлении, через которые должна проходить окружность.

5. Полуокружность по двум точкам.

Необходимо указать две точки, которые будут концами диаметра окружности.

6. Дуга по центру и двум точкам.

Строит дугу окружности. Необходимо вначале указать центр окружности, а потом начало и конец дуги.

7. Дуга по трём точкам.

Необходимо указать три точки окружности. При этом первая точка будет указывать начало дуги, а третья её конец.

8. Сектор по центру и двум точкам.

Инструмент аналогичен инструменту "Дуга по центру и двум точкам", только строит сектор.

9. Сектор по трём точкам.

Инструмент аналогичен инструменту "Дуга по трём точкам", только строит сектор.

Конические сечения



Рис. 9

1. Эллипс (рис. 9).

Данный инструмент строит эллипс по трём точка. Укажите две точки, которые являются фокусами эллипса, и точку на самой линии.

2. Гипербола.

Гипербола строится аналогично эллипсу. Вначале указываются фокусы гиперболы, а потом точка на самой гиперболе.

3. Парабола.

Необходимо указать точку и директрису параболы.

4. Коника по пяти точкам.

Пять точек плоскости однозначно определяют кривую второго порядка. Можно указать 5 точек линии и GeoGebra автоматически построит параболу, гиперболу или эллипс.

Измерения



Рис. 10

1. Угол (рис. 10).

Задаёт угол по трём точкам. Угол по умолчанию задаётся против часовой стрелки.

---

2. Угол заданной величины.

Задав две точки угла, Вам будет предложено ввести значение третьего угла. Для ввода значений можно использовать градусную меру (для добавления символа градус используется комбинация клавиш Alt+O, в Mac OS Ctrl+O), радианную меру (символ числа П можно добавить горячими клавишами Alt+P, Mac OS Ctrl+P) или сделать угол зависимым от некоторой переменной.

3. Расстояние или длина.

Выводит на экран длину линии.

4. Площадь.

Выводит на экран площадь фигуры.

5. Наклон прямой.

Выводит на экран наклон прямой в точке.

6. Создать список.

Создаёт список из выделенных объектов.

Преобразования



Рис. 11

1. Отражения относительно прямой (рис. 11).

Выберите на чертеже объект и прямую. Вы получите образ вашего объекта при симметрии относительно прямой. Изменять образ нельзя, но изменяя прообраз, он будет изменяться автоматически.

2. Отражения относительно точки.

Необходимо выбрать на чертеже объект и точку.

3. Отражение относительно окружности.

Необходимо выбрать на чертеже объект и окружность.

4. Поворот вокруг точки на угол.

Выбрав объект можно повернуть его на введённый с клавиатуры угол, относительно некоторой точки.

5. Параллельный перенос по вектору.

Выберите объект и вектор, на который будите его переносить.

6. Гомотетия относительно точки.

Необходимо выбрать объект, точку, которая будет центром гомотетии, и ввести с клавиатуры коэффициент гомотетии.

Специальные объекты



Рис. 12

1. Надпись (рис. 12).

Вывод текста в поле отображения. Более подробно об этом инструменте пойдёт речь в разделе: "Вывод текста"

2. Вставить изображение.

Добавляет графическое изображение. Необходимо указать левую нижнюю точку изображения и выбрать нужный Вам файл. Поддерживает форматы: bmp, jpg, png, gif и tif.

---

3. Карандаш.

Рисует на Графическом отображении. Просто зажимаете левую кнопку мыши и двигаете ей. Не стоит закрашивать пропуски в ручную, после того как вы отпустите левую кнопку мыши, они автоматически уберутся.

4. Отношения объектов.

Выводит во всплывающем окне информацию о отношении двух фигур: их идентичности, принадлежности.

5. Калькулятор Вероятностей.

Открывает дополнительно окно для расчёта вероятностей.

6. Исследователь функций.

Выводит в дополнительном окне информацию о функции: точки максимума и минимума, корни и т.д.

Действия над объектами



Рис. 13

1. Ползунок (рис. 13).

Добавление на графическое представление ползунка, точки на горизонтальном отрезке, которая может менять своё значение. Более подробно об этом инструменте пойдёт речь в уроке "Ползунок"

2. Флажок отображения/скрытия объектов.

Добавляет на графическое представление флажок, который отвечает за видимость объектов на форме. Более подробно разберём его работу в одном из следующих уроков.

3. Кнопка.

Добавление на графическое представление программируемую кнопку. Этот объект выходит за рамки курса GeoGebra (для начинающих). Он будет описан в курсе GeoGebra (эксперт).

4. Окно ввода.

Добавление на графическое представление окно ввода числового значения.

Общие



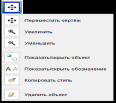
Рис. 14

1. Переместить чертёж (рис. 14).

Данный инструмент позволяет изменить видимость графического представления, за счёт сдвига видимой области при помощи курсором мыши.

2. Увеличить \ Уменьшить.

Эти два инструмента изменяют масштаб графического представления. Кроме этого, масштаб можно изменять колёсиком мыши.

3. Показать/скрыть объект.

Позволяет менять видимость выбранного объекта. Необходимо выбрать объекты, которые вы хотите скрыть, после чего сменить инструмент на другой.

---

4. Показать/скрыть обозначения.

Позволяет менять видимость обозначения выбранного объекта.

5. Копировать стиль.

Позволяет применять стиль отображения объекта (цвет, толщина и т.д.) на другие объекты. Необходимо выбрать вначале объект, чей стиль вы будите копировать, а потом объекты, на которые вы будите копировать. Для отмены стиля, нажмите на первый объект второй раз.

6. Удалить объект.

Удаляет объект по нажатию левой кнопкой мыши на него.



Глава 2. Решения задач школьного курса планиметрии с применением математического пакета Geogebra

§1. Основные теоретические сведения из школьного курса планиметри

1   2   3   4   5   6   7

---

1.1. Углы и прямые

Часть прямой линии, ограниченная с одной стороны и неограниченна с другой, называется полупрямой или лучом.

Часть прямой линии, ограниченная с двух сторон, называется отрезок.

Углом называется фигура, образованная двумя лучами, исходящими из одной точки. Эту точку называют вершиной, а лучи – сторонами угла.

Угол называется развернутым, если его стороны являются дополнительными прямыми одной прямой.

Основной единицей измерения углов является угол в один градус (обозначается ), равный части развернутого угла.

Развернутый угол равен .

Два угла называется смежными, если у них одна сторона общая, а две другие стороны этих углов являются дополнительными полупрямыми.

Сумма смежных углов равен .

Взаимное расположение прямых на плоскости.

Возможны следующие случаи:

• 
  пересечение;
  
• 
  параллельность;
  
• 
  совпадение.
  

Прямые, которые пересекаются под прямым углом, называется взаимно перпендикулярными. Через каждую точку можно провести только одну перпендикулярную к ней прямую.

Прямые, которые не пересекаются, называются параллельными. Через каждую точку плоскости можно провести прямую, параллельную данной прямой, и притом только одну.

Признак параллельности прямых:

• 
  если прямая параллельна прямым и , то прямые и параллельны;
  
• 
  если внутренние накрест лежащие углы прямых и с секущей равны или сумма внутренних односторонних углов равна , то прямые и параллельны.
  

1.2. Многоугольник

Многоугольником

---

Смотрите также файлы

• Вариант 1 Как называется 19 век в русской литературе.docx

• Интервал между текстом и таблицей не менее 12 пунктов, но не более 24 пунктов.docx

• Введение обзор литературы.docx

• Рабство в Древнем Риме.docx

• Разработка алгоритмов и программ с использованием массивов в среде С.docx