Файл: В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи.doc

Следовательно, можно принять приемочное число равным A₀ = 2 с риском поставщика или равным A₀ = 3 с риском поставщика .

В том случае, если требуется фактический риск приблизить к заданному, то это можно сделать при постоянном объеме партии и доле дефектных устройств, варьируя объемами выборки и приемочными числами.

3. Браковочное число A₁ определяется аналогично приемочному числу с той лишь разницей, что в данном случае нужно руководствоваться формулой для определения (приведена выше в задаче) и суммировать вероятности f–биноминального распределения до величины

Определяем вероятности f–биноминального распределения

,





Так как

R( d ≤ 1 ) = 0,010 + 0,058 = 0,068

R( d ≤ 2 ) = 0,010 + 0,058 + 0,137 = 0,205,

то, очевидно, целесообразно считать браковочным числом A₁ = 2, тогда риск заказчика будет более близким к установленному.

Пример 4.2.5. Последовательному контролю надежности подлежит партия, состоящая из N = 100 невосстанавливаемых изделий. Партия считается хорошей при доле дефектных изделий q₀ = 0,05 и плохой – при q₁ = 0,10. Риск поставщика равен риску заказчика и составляет 0,1. Требуется определить приемочные (m_пр) и браковочные (m_бр) числа испытаний при числе дефектных изделий d_m = 0, 1, 2, 3, 4 и 5, а также построить график контроля по характеристическим точкам и принять решение в случае появления четырех отказов при 25 испытаниях.

Решение. Так как общий объем исследуемой совокупности мал, необходимо осуществлять контроль по f-биноминальному плану. Для того, чтобы определить приемочные и браковочные числа и построить график контроля необходимо произвести следующие вычисления.

1. Определяем число дефектных изделий в партии при нулевой и альтернативной гипотезах:

---

;
2. Находим значения оценочных нормативов А и В:


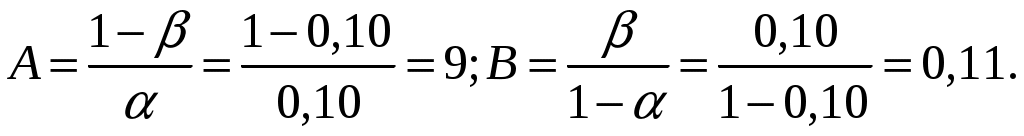
3. Для определения характеристических точек графика плана подсчитываем значения c и r:



4. Определяются приемочные числа по выражению

, в которое подставляем постоянные величины N, B, c, r и вычисляем переменную для каждого числа дефектных изделий величину.

Следовательно,

; ;

,

; ;



и т. д.

Для подсчета браковочных чисел используется выражение

. Очевидно, что эта формула имеет смысл при

, что в соответствии с таблицей биноминальных коэффициентов имеет место при d_m ≥ 3. Для d = 3 ;

и т. д.

После расчета всех приемочных и браковочных чисел результаты представлены в таблице 4.2.1

Таблица 4.2.1

dm	0	1	2	3	4	5
mпр не менее	36	44	53	61	69	78
mбр не более	-	-	-	7	27	49

---

5. Определяются характеристические точки для построения графика плана:

а) d_m = 0, ;

б) d_m = D₀ = 5, ;

в) d_m = ; m = N= 100

Для построения графика плана строим прямоугольные оси координат с ординатами d_m = 0, 1, 2, …., 10 и абсциссами m = 1,2, 3, …, 100 и отмечаем

точки а ,б и в. Далее точку в соединяем с точками а и б.

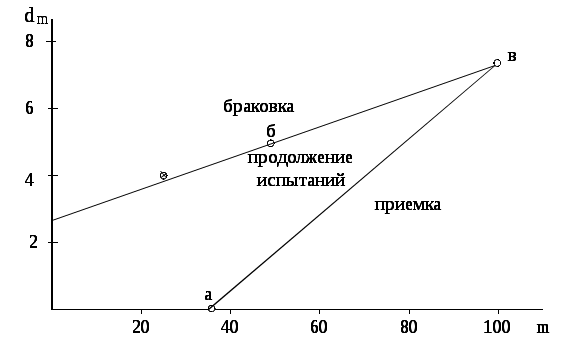
Рисунок 4.1. График контроля


Заданная по условию примера рабочая точка d = 4, m = 25 попадает в область браковки (смотри график контроля рис.4.1). Следовательно, партию можно забраковать и испытания прекратить.

Правильность решения можно проверить по правилу браковки:



С этой целью посчитаем



Так как 14,9 > 9, то партия бракуется.

---

4.3 Индивидуальные задания по теме «Оценка и контроль надежности устройств по результатам испытаний»
Задача 4.3.1. По плану [ n, Б, t₀ ] испытано n = 100 изделий в течение t₀ = 100 часов. При этом возникло 48 отказов. Известно, что распределение времени до отказа экспоненциальное. Оценить нижнюю доверительную границу средней наработки до отказа с вероятностью α₁ = 0,95.

Задача 4.3.2. По плану [n, Б,d ] были испытаны 20 электродвигателей. После 6 – го запланированного отказа, наступившего через 180 часов после начала испытаний, испытания приостановлены. Требуется оценить интенсивность отказов и найти её верхнюю границу с вероятностью α₂ = 0,95.

Задача 4.3.3. В результате испытаний 12 комплектов аппаратуры были получены следующие значения наработки на отказ в часах: 16,8; 18,4; 22,3; 22,7; 23,1; 25,5; 26,4; 29,2; 30,3; 32,5; 33,3; 38,1; 42,2. Определить оценку средней наработки отказа Т ^* и дисперсию σ ², а также нижнюю границу Т и верхнюю границу σ с вероятностью α = 0,9.

Задача 4.3.4. План испытаний [n, Б, n]. При испытании n = 15 устройств до выхода из строя получены следующие значения до наработки на отказ в часах: t₁ = 30 ч, t₂ = 35 ч, t₃ = 50 ч, t₄ = 60 ч, t₅ = 80 ч, t₆ = 150 ч, t₇ = 200 ч, t₈ = = 220 ч, t₉ = 250 ч, t₁₀ = 280 ч, t₁₁ = 300 ч, t₁₂ = 320 ч, t₁₃ = 380 ч, t₁₄ = 400 ч, t₁₅ = 600 ч.

Требуется определить:

1. Оценку λ ^* интенсивности отказов λ.

2. Верхнюю доверительную границу с доверительной вероятностью α₂ = 0,90.

3. Двухсторонний доверительный интервал для λ при α = 0,90 и β₁ = β₂ = 0,05.

4. Оценку средней наработки до отказа Т и его нижнюю границу с вероятностью 0,90.

Задача 4.3.5. В результате испытаний 100 интегральных схем (ИС), которое продолжалось t₀ = 5000 ч, вышло из строя 5 ИС с наработкой до отказа в часах соответственно t₁ = 500 ч, t₂ = 1500 ч, t₃ = 2500 ч, t₄ = 3000 ч, t₅ = 4500 ч. Определить среднюю наработку на отказ ИС и среднее квадратическое отклонение, полагая, что срок службы ИС подчиняется нормальному закону.

---

Задача 4.3.6. План испытаний [n, Б, n]. При испытании n = 10 устройств до выхода их из строя получены следующие значения наработки в часах: t₁ = 60 ч, t₂ = 70 ч, t₃ = 90 ч, t₄ = 160 ч, t₅ = 190 ч, t₆ = 300 ч, t₇ = 400 ч, t₈ = = 580 ч, t₉ = 800 ч, t₁₀ = 1100 ч.

Требуется определить:

1. Оценку интенсивности отказов λ.

2. Верхнюю доверительную границу λ_В с доверительной вероятностью α₂ = 0,90.

3. Двухсторонний доверительный интервал для λ при α = 0,9 и β₁ = β₂ = 0,05.

4. Оценку средней наработки до отказа Т ^* и его нижнюю границу с вероятностью 0,9.

Задача 4.3.7. При испытании электронных приборов по плану [n, Б,  d], где n = 50, а d= 101, через 696 часов испытаний наступил 101- ый отказ, время наступления предыдущих отказов не регистрировалось. Определить среднюю наработку до отказа и найти его нижнюю границу с доверительной вероятностью α₁ = 0,99, исходя из экспоненциального закона распределения отказов.

Задача 4.3.8. Испытано 8 экземпляров ЭЦВМ по плану [n, Б, t₀]. Испытание продолжалось в течение времени t₀ = 100 часов, и при этом было зарегистрировано 8 отказов. Отказы ЭЦВМ мгновенно устранялись. Найти доверительный интервал значений интенсивности отказов с доверительной вероятностью для нижней границы α₁ = 0,90 и для верхней α₂ = 0,995; определить доверительную вероятность для двухстороннего интервала.

Задача 4.3.9. При испытаниях по плану [n = 50, Б, d = 6] получены следующие значения наработки отказов устройств: 80, 150, 250, 300, 350 и 450 часов. Отказавшие устройства не восстанавливаются. Требуется найти оценку интенсивности отказов λ и доверительный интервал с вероятностью α = 0,90 при β₁ = β₂ = 0,05.

Задача 4.3.10. План испытаний [n, Б, t₀]. За время испытания по плану [n = 40, Б, t₀ = 400 ч] отказало d = 5 устройств, причём отказавшие устройства проработали до выхода из строя соответственно 150, 200, 320, 350, 400 час. Требуется определить оценку интенсивности отказов λ и двухсторонний доверительный интервал для α = 0,8 при β₁ = β₂ = 0,10.

Задача 4.3.11. При испытании по плану [n = 120, Б, t₀ = 120] зарегистрировано 6 отказов. Отказавшие устройства мгновенно заменялись исправными. Требуется определить оценку интенсивности отказов, верхнюю доверительную границу интенсивности отказов λ с вероятностью 0,99 и доверительный интервал для α = 0,90 при β

---