ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 216
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
I. Организационный момент.
II. Каллиграфическая минутка.
28 28 28 28 28
30 30 30 30 30
III. Устный счёт.
1. Круговые примеры.
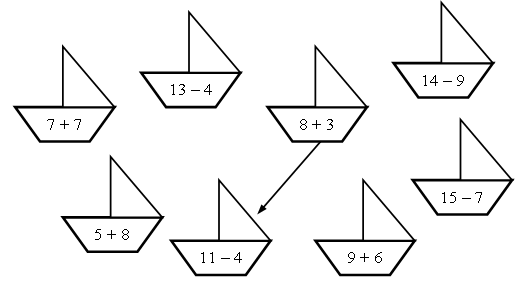
2. Какое число пропущено?
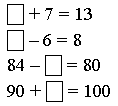
3. Который час?
Работа проводится по заданию 6 (с. 39 учебника, часть 1), его лучше вынести на доску.
– Какие из этих часов показывают правильное время, если сейчас без 15 минут 8 часов? (Правильное время показывают вторые часы.)
– На сколько минут спешат или отстают другие часы? (Первые часы спешат на 5 минут, третьи часы отстают на 20 минут.)
IV. Работа над новым материалом.
Учитель предлагает учащимся рассмотреть сумму чисел, записанную на доске:
5 + 3 + 2 = 10
– Как по-разному можно найти значение данной суммы?
С п о с о б I. Сначала к первому слагаемому 5 прибавим второе слагаемое 3.
(5 + 3) – получим 8.
Затем к числу 8 прибавим третье слагаемое 2.
(5 + 3) + 2 – получим 10.
С п о с о б II. Сначала ко второму слагаемому 3 прибавим третье слагаемое 2.
(3 + 2) – получим 5.
Затем полученное число 5 прибавим к первому слагаемому 5.
5 + (3 + 2) – получим 10.
– Какой способ показался вам более удобным?
Далее отрабатывается прием группировки слагаемых при решении следующих выражений:
1 + 9 + 5
2 + 7 + 3
6 + 1 + 9
Ученики выбирают наиболее удобный способ решения выражений.
Н а п р и м е р:
(1 + 9) + 5 = 10 + 5 = 15
2 + (7 + 3) = 2 + 10 = 12
6 + (1 + 9) = 6 + 10 = 16
После этой работы учитель просит детей сформулировать вывод и сравнить его с правилом, данным в учебнике на с. 38 (часть 1).
Затем учитель предлагает учащимся сравнить суммы, записанные на доске:
4 + (1 + 3)
(4 + 1) + 3
(4 + 3) + 1
1 + (4 + 3)
– Что хотите сказать?
– Как вы думаете, значения этих сумм равны?
– Почему так считаете?
– Какой закон сложения применяли в 3-й и 4-й суммах? (Переместительный.)
– Подумайте, правильно ли будет сказать: если нужно сложить несколько чисел, то их можно складывать в любом порядке, значение суммы при этом не изменится. (Да.)
Далее с подробным устным объяснением выполняется задание 3 (с. 39 учебника, часть 1), в котором дети сравнивают выражения, объясняют, как каждое следующее выражение получено из предыдущего, выбирают наиболее удобный способ решения того или иного выражения.
Физкультминутка
V. Работа над задачами.
Учащиеся читают текст задачи 4 (с. 39 учебника, часть 1), находят условие и вопрос, называют данные и искомое числа, затем составляют схему-чертёж и решают задачу. После того как задача решена, к ней составляются две обратные задачи.
( Экскурсия вместе с дорогой в парк и обратно заняла 1 час. На дорогу было потрачено 20 минут. Сколько длилась экскурсия?
Экскурсия вместе с дорогой в парк и обратно заняла 1 час. Экскурсия длилась 40 минут. Сколько времени было потрачено на дорогу?)
VI. Работа с геометрическим материалом.
– Вспомните, что называется периметром многоугольника.
– Как найти периметр многоугольника?
– Найдите периметр четырёхугольника, две стороны которого имеют длину по 30 миллиметров каждая, а остальные стороны – по 20 миллиметров каждая.
(Запись на доске и в тетрадях учеников:
Рчетырехугольника = 30 мм + 30 мм + 20 мм + 20 мм,
Рчетырехугольника= 100 мм = 10 см.)
Затем учитель предлагает ученикам рассмотреть кораблик, изображённый на полях с. 39 (учебник, часть 1).
– Что хотите сказать?
– Из каких геометрических фигур состоит кораблик?
– Какой фигуры из приведённых ниже не хватает, чтобы получился такой же кораблик? (Не хватает треугольника, изображающего мачту корабля; этот треугольник жёлтого цвета.)
VII. Итог урока.
– Чему научил вас урок?
– Чем важны приобретённые сегодня знания?
– Какова ваша роль на уроке?
Тема: Работа с текстовыми задачами. Задачи, содержащие отношения «больше (меньше) на…»
Цели: продолжать работу над задачами и выражениями изученных видов; формировать умение учащихся группировать слагаемые, находить удобный способ решения выражений; отрабатывать умение находить периметр многоугольника; развивать логическое мышление, внимание, наблюдательность.
Ход урока
I. Организационный момент.
II. Каллиграфическая минутка.
19 19 19 19 19
91 91 91 91 91
– Что хотите сказать?
– Одинакова ли роль цифры 1 (9) в числах 19 и 91?
III. Устный счёт.
1. «Набери число».
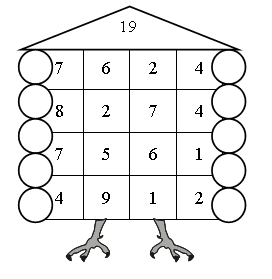
2. Задание на смекалку.
В семье трое детей: Женя, Валя и Саша: 2 мальчика и 1 девочка.
Среди имён Женя и Валя есть имя одного мальчика. Среди имён Саша и Женя тоже есть имя одного мальчика.
Как зовут девочку? (Девочку зовут Валя.)
IV. Решение выражений.
– Рассмотрите выражения, записанные на доске:
57 – 7 – 1 20 – (2 + 8) 76 – 6 – 1 11 – 7
14 – 9 6 + 7 19 + (9 – 8) 5 + 8
– Разделите выражения на группы так, чтобы в каждой группе оказались похожие выражения.
14 – 9 6 + 7 20 – (2 + 8) 5 7 – 7 – 1
11 – 7 5 + 8 19 + (9 – 8) 7 6 – 6 – 1
После того как выражения разбиты на группы, ученики находят их значения. Третий и четвёртый столбики выполняются с подробным объяснением.
Затем учащиеся решают выражения из задания 1 (с. 40 учебника, часть 1). Желательно, чтобы выражения были записаны на доске.
Дети, применяя правило, с которым познакомились на прошлом уроке, находят самый удобный способ решения выражений. Задание выполняется с комментированием.
Н а п р и м е р:
50 + 6 + 30
Удобно к пятидесяти прибавить сначала 30, а затем к полученному результату прибавить 6.
Сумма чисел 50 и 30 равна 80. К 80 прибавить 6 – будет 86.
Значение суммы чисел 50, 6 и 30 равно 86.
7 +20 + 3 + 70
Удобно к семи прибавить три, а к семидесяти прибавить двадцать, после чего полученные результаты сложить.
Сумма чисел 7 и 3 равна 10. Сумма чисел 70 и 20 равна 90. К 90 прибавить 10 – получим 100.
Значение суммы чисел 7, 20, 3 и 70 равно 100.
И т. д.
Физкультминутка
V. Работа над задачами.
Учащиеся читают текст задачи 4 (с. 40 учебника, часть 1) и соотносят её со схемой-чертежом, приведенной ниже.
– Что в задаче известно?
– Как это показано на чертеже?
– Что требуется узнать?
– Как это показано на чертеже?
– Запишите решение задачи.
– Сформулируйте и запишите ответ задачи.
Затем учащиеся читают задачу 45 (с. 40 учебника, часть 1) и сопоставляют её со схемой-чертежом.
– Чем похожи задачи?
– Чем отличаются? (Первая задача простая, вторая – составная.)
– Рассмотрите выражения, записанные ниже.
– Что узнаем, если к 30 прибавим 20? (Число каменных домов.)
– Что узнаем, решив второе выражение? (Сколько всего домов в дачном посёлке.)
– Какое из выражений является решением задачи? (Второе.)
– Запишите его и решите.
– Дайте ответ на вопрос задачи.
VI. Работа с геометрическим материалом.
– Как называется линия, изображённая на полях с. 40 учебника? (Ломаная.)
– Что вы можете сказать про данную ломаную линию? (Эта ломаная незамкнутая, она состоит из трёх звеньев.)
– Найдите длину этой ломаной. (3 + 4 + 5 = 12 см.)
– Начертите треугольник, периметр которого равен двенадцати сантиметрам.
– Какие треугольники у вас получились?
VII. Задание по образцу.
В заключение урока дети выполняют задание на полях с. 38 (учебник, часть 1): «Начерти, продолжи и раскрась узор».
VIII. Итог урока.
– Чему научил вас урок?
– Какое задание было для вас самым интересным?
– А какое самым трудным?
– Что помогло справиться с трудностями?
Тема: Арифметические действия. Использование свойств арифметических действий в вычислениях (перестановка и группировка слагаемых в сумме)
Цели: продолжать работу над задачами изученных видов; развивать умение решать составные задачи выражением; продолжать формировать умение находить значения выражений удобным способом, определять разрядный состав числа; развивать логическое мышление учеников.
Ход урока
I. Организационный момент.
II. Каллиграфическая минутка.
38 38 38 38 38
48 48 48 48 48
– Что хотите сказать?
III. Устный счёт.
1. Представьте в виде суммы разрядных слагаемых:

2. Поставьте скобки так, чтобы равенства стали верными:
13 – 9 – 4 = 0
11 – 3 + 4 = 12
14 – 5 + 4 = 5
12 – 3 + 1 = 8
Решение:
(13 – 9) – 4 = 0
(11 – 3) + 4 = 12
14 – (5 + 4) = 5
12 – (3 + 1) = 8
3. Задача на смекалку.
Во вторник ёж принёс на три гриба больше, чем в среду, и на два гриба больше, чем в четверг. В какой день, в среду или четверг, ёж принёс больше грибов? (В четверг.)
IV. Работа над задачами.
Учитель читает текст из задания 5 (с. 41 учебника, часть 1).
– Я прочитала вам задачу? (Нет.)
– Почему так считаете? (Отсутствует вопрос.)
– Поставьте вопрос, соответствующий данному условию. (Сколько игроков было на поле в начале игры?)
– Сделайте краткую запись.
Один ученик выполняет работу на доске:
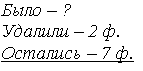
– Решите задачу и запишите ответ.
(7 + 2 = 9 (ф.)
О т в е т: 9 футболистов было на поле.)
Физкультминутка
Разбирая задачу 6 (с. 41 учебника, часть 1), учащиеся под руководством учителя составляют к ней схему-чертёж, после чего самостоятельно записывают решение и ответ задачи.
14 – 6 = 8 (м.)
О т в е т: 8 мальчиков.
Или:
О т в е т: 8 мальчиков приняли участие в турнире.
К задаче 7 (с. 41 учебника, часть 1), после того как учащиеся выделят условие и вопрос, назовут данные и искомое числа, составляется выражение.
Р е ш е н и е:
12 – (6 + 2) = 4
О т в е т: 4 партии Костя сыграл вничью.
V. Составление равенств и неравенств.
На доске записаны выражения из задания 2 (с. 41 учебника, часть 1).