Добавлен: 04.12.2023
Просмотров: 998
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
18.4. Материальная точка совершает колебания по закону синуса с амплитудой 10 см, частотой 2 Гц и начальной фазой 30 градусов. Полная энергия колеблющейся точки 0.077 Дж. Через какой промежуток времени от начала движения кинетическая энергия станет равной потенциальной? Построить график зависимости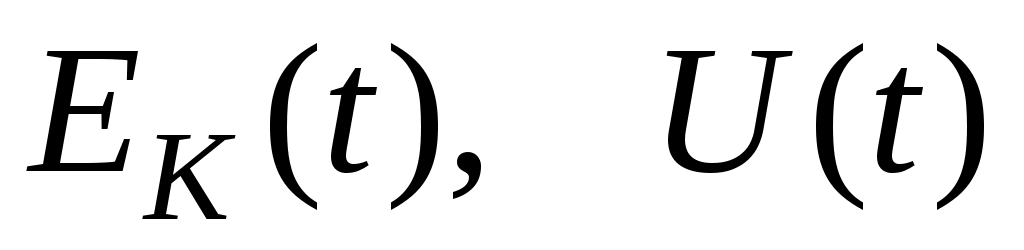 в диапазоне времен от 0 до
в диапазоне времен от 0 до  .
.
18.5. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями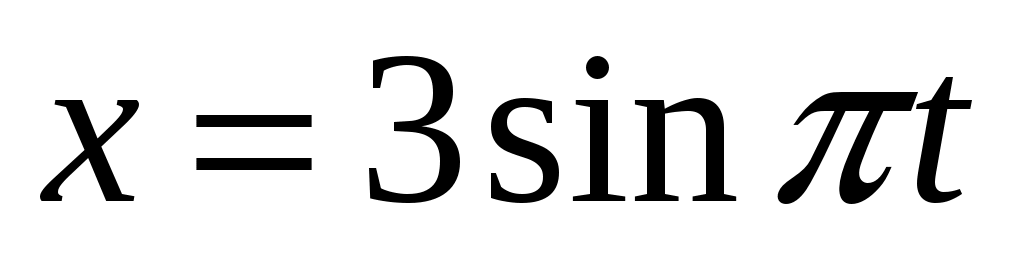 см и
см и 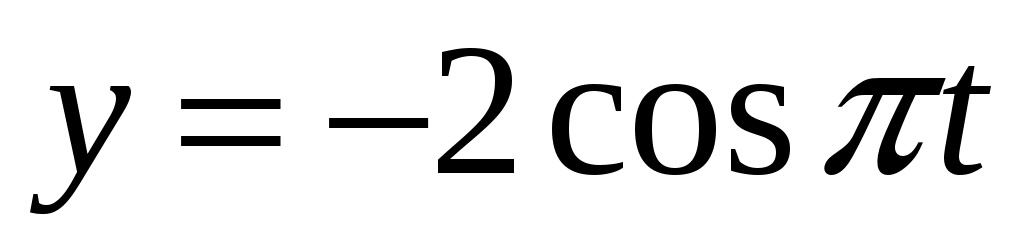 см. Найдите уравнение траектории точки. Определите скорость и ускорение точки в момент времени 0.5 с. Построить траекторию движения точки
см. Найдите уравнение траектории точки. Определите скорость и ускорение точки в момент времени 0.5 с. Построить траекторию движения точки 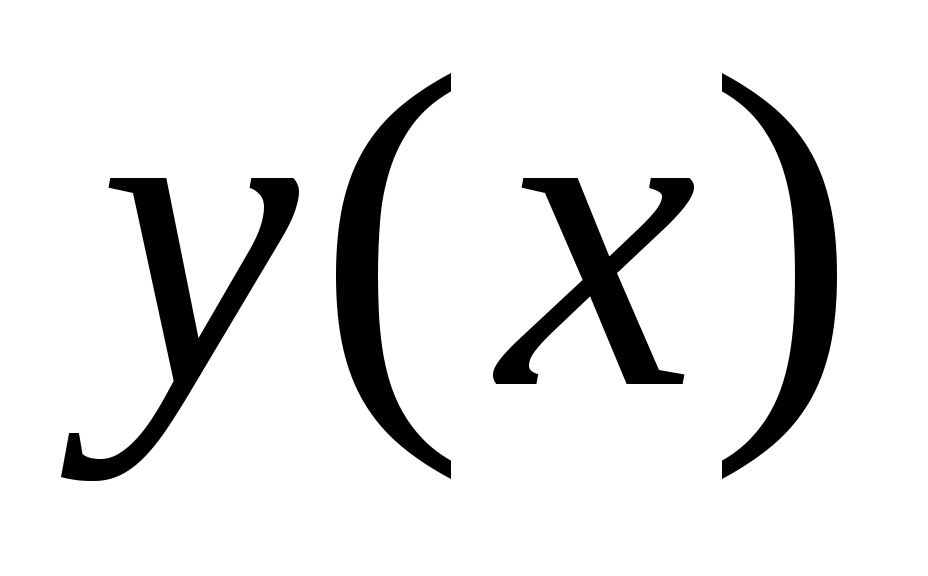 .
.
18.6. Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0 с частотой 4.00 с-1. В некоторый момент времени координата частицы равна 25 см и ее скорость 100 см/с. Найти координату и скорость частицы через 2.4 с после этого момента времени. Построить график зависимости (фазовый портрет)
(фазовый портрет)
18.7. Определите амплитуду гармонических колебаний материальной точки, если полная энергия колеблющейся точки 0.04 Дж, а максимальная сила, действующая на точку, равна 2 Н. Привести поясняющий рисунок и указать основные параметры
18.8. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты так
так 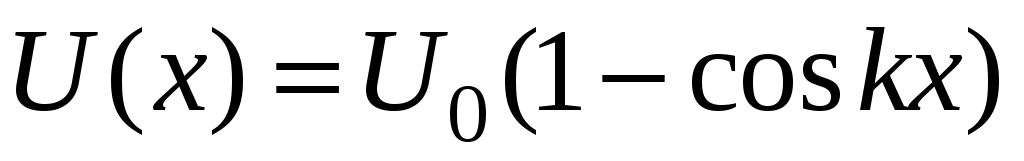 , где
, где 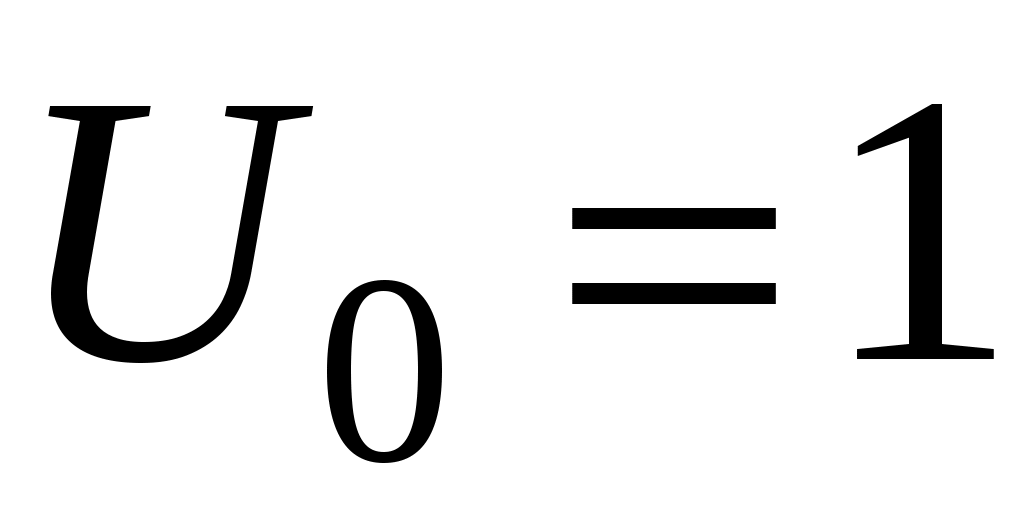 Дж и
Дж и 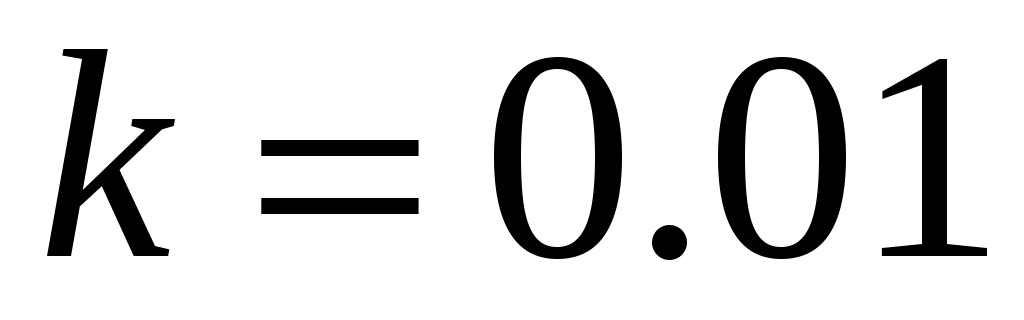 м-1 – постоянные. Найти циклическую частоту и период малых колебаний частицы около положения равновесия. Построить график зависимости
м-1 – постоянные. Найти циклическую частоту и период малых колебаний частицы около положения равновесия. Построить график зависимости  .
.
18.9. На доске лежит груз массой 10 кг. Доска совершает гармонические колебания по закону косинуса в вертикальном направлении с периодом 0.5 с и амплитудой 2 см. Определите величину давления
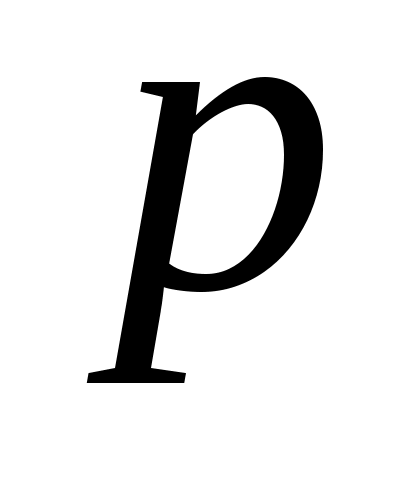 груза на доску в момент времени 2 с и полную энергию колеблющегося груза. Начальная фаза колебаний равна нулю. Построить график зависимости
груза на доску в момент времени 2 с и полную энергию колеблющегося груза. Начальная фаза колебаний равна нулю. Построить график зависимости 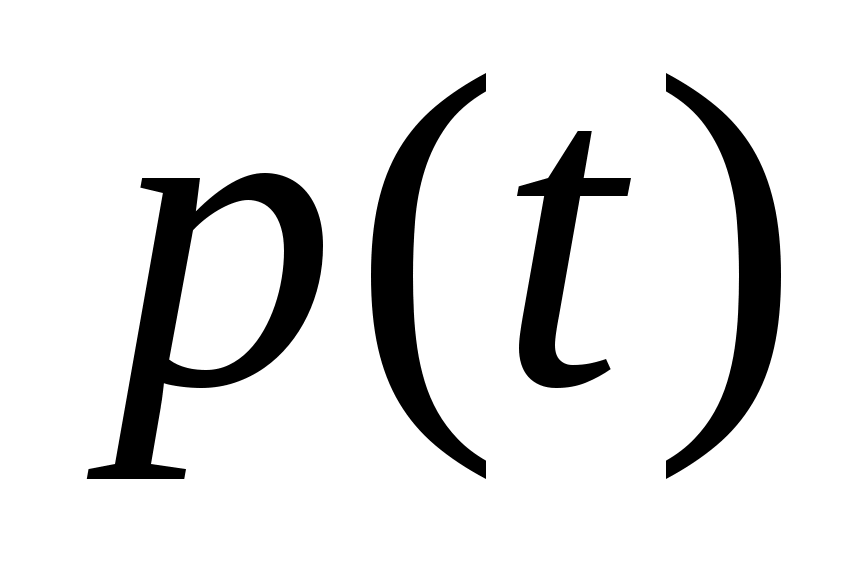 .
.
18.10. Найти период малых поперечных колебаний шарика массы 40 г, укрепленного на середине натянутой струны длины 1 м. Силу натяжения струны считать постоянной и равной 10 Н. Массой струны и силами тяжести пренебречь. Построить график зависимости .
.
18.11. Уравнение изменения силы тока в колебательном контуре дано в виде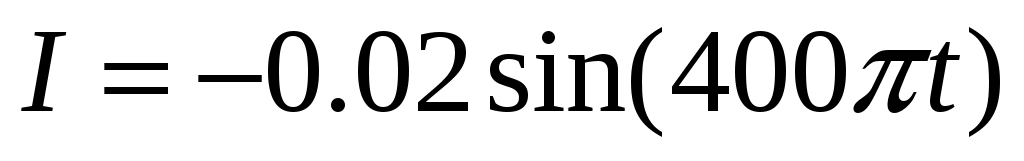 А. Индуктивность катушки 1 Гн. Найдите 1) период колебаний, 2) емкость конденсатора, 3) максимальную разность потенциалов на обкладках конденсатора, 4) максимальную энергию электрического поля, 5) максимальную энергию магнитного поля. Построить векторную диаграмму напряжений и привести графики
А. Индуктивность катушки 1 Гн. Найдите 1) период колебаний, 2) емкость конденсатора, 3) максимальную разность потенциалов на обкладках конденсатора, 4) максимальную энергию электрического поля, 5) максимальную энергию магнитного поля. Построить векторную диаграмму напряжений и привести графики 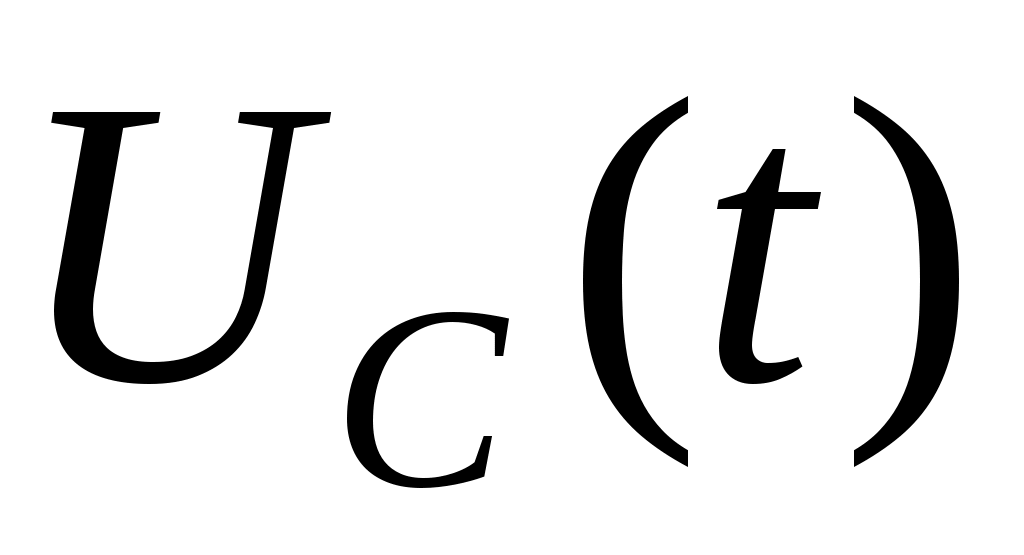 и зависимость энергии в
и зависимость энергии в 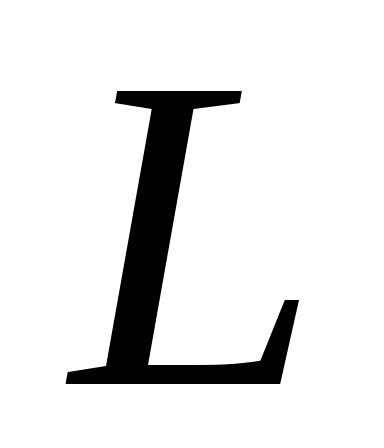 и
и 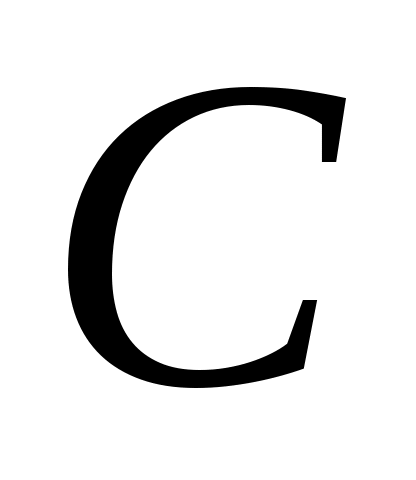 от времени.
от времени.
18.12. Колебательный контур имеет индуктивность 0.23 Гн, емкость конденсатора 7 мкФ. Сопротивление контура 40 Ом. Конденсатор заряжен 0.56 мКл. Найдите: а) период колебаний, б) логарифмический декремент затухания колебаний λ. Напишите уравнение зависимости разности потенциалов на обкладках конденсатора от времени. Построить векторную диаграмму напряжений и привести графики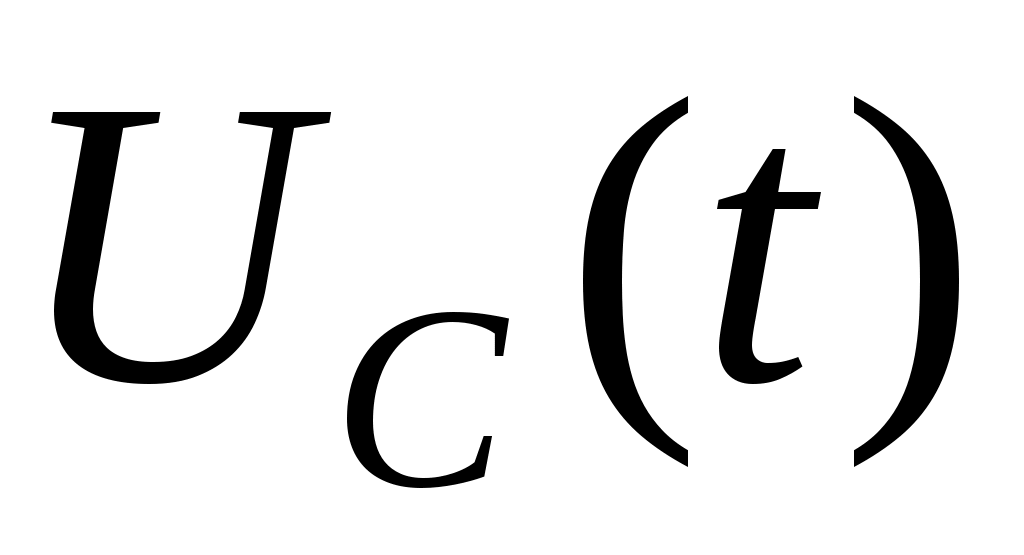 и зависимость энергии в
и зависимость энергии в 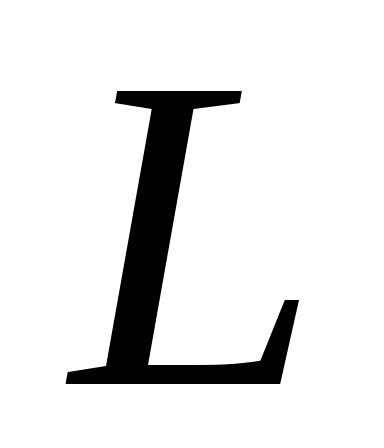 и
и 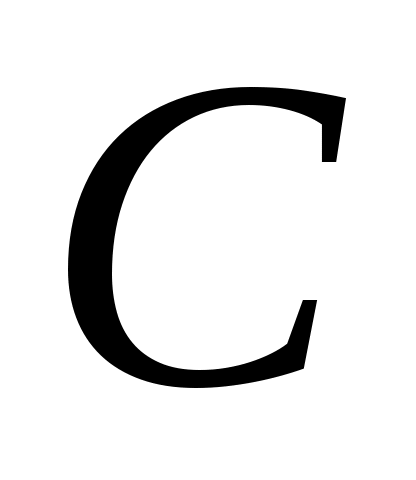 от времени.
от времени.
18.13. Заряженный конденсатор емкостью 0.35 мкФ подключили к катушке индуктивностью 0.25 мГн. Через какое время после подключения катушки энергия электрического поля станет равной энергии магнитного поля катушки? Построить графики энергий. Активным сопротивлением контура пренебречь.
18.14. В колебательном контуре, состоящем из конденсатора и катушки индуктивностью 2.5 мГн, происходят электромагнитные колебания, при которых максимальная сила тока 10 мА. Определить емкость конденсатора, если максимальная разность потенциалов на его обкладках достигает 50 В, а активным сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики
 и зависимость энергии в
и зависимость энергии в  и
и  от времени.
от времени.
18.15. Определить частоту собственных колебаний колебательного контура, который состоит из конденсатора емкостью 2 мкФ и катушки длиной 10 см и радиусом 1 см, содержащим 500 витков. Учесть, что происходят электромагнитные колебания, при которых максимальная сила тока в контуре 10 мА. Сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики и зависимость энергии в
и зависимость энергии в  и
и  от времени.
от времени.
18.16. Колебательный контур имеет индуктивность 1.6 мГн, емкость конденсатора 0.04 мкФ и максимальную разность потенциалов на обкладках конденсатора 200 В. Чему равна максимальная сила тока в контуре? Активное сопротивление контура мало. Построить векторную диаграмму напряжений и привести графики и зависимость энергии в
и зависимость энергии в  и
и  от времени.
от времени.
19.Затухающие колебания
Пример 19.1. Горизонтальное колебательное движение бруска при наличии сухого трения.
Пружинный маятник представляет собой брусок массой , лежащий на горизонтальной плоскости, соединенный горизонтальной пружиной с вертикальной стенкой. Брусок в начальный момент времени сместили из положения равновесия
, лежащий на горизонтальной плоскости, соединенный горизонтальной пружиной с вертикальной стенкой. Брусок в начальный момент времени сместили из положения равновесия 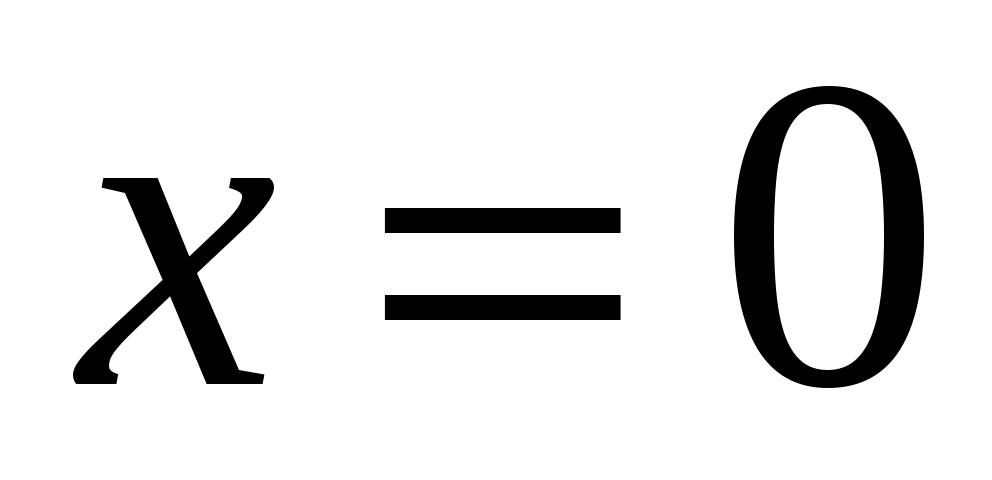 на
на 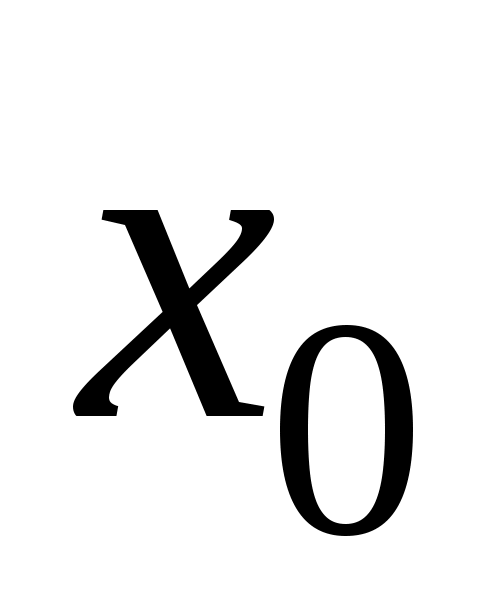 , так что пружина растянулась, затем отпустили с нулевой скоростью. Сколько колебаний совершит брусок до момента остановки, если коэффициент сухого трения скольжения равен
, так что пружина растянулась, затем отпустили с нулевой скоростью. Сколько колебаний совершит брусок до момента остановки, если коэффициент сухого трения скольжения равен  ?
?
Для численных расчетов принять кг,
кг, 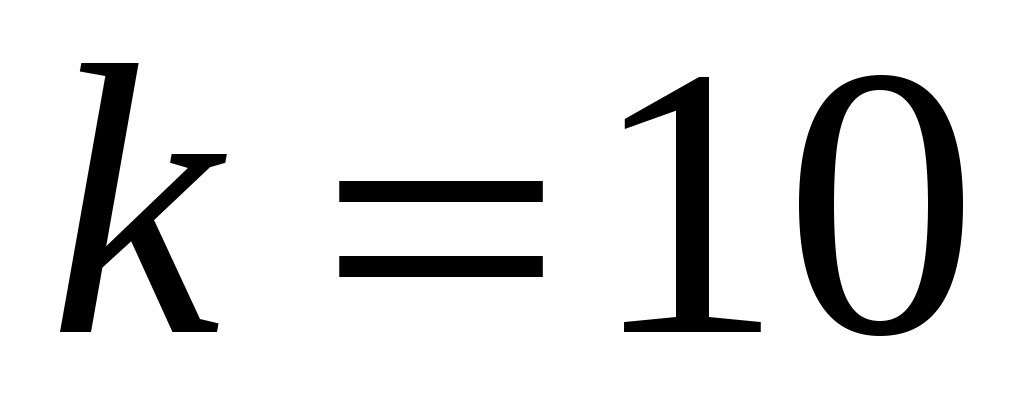 Н/м,
Н/м, 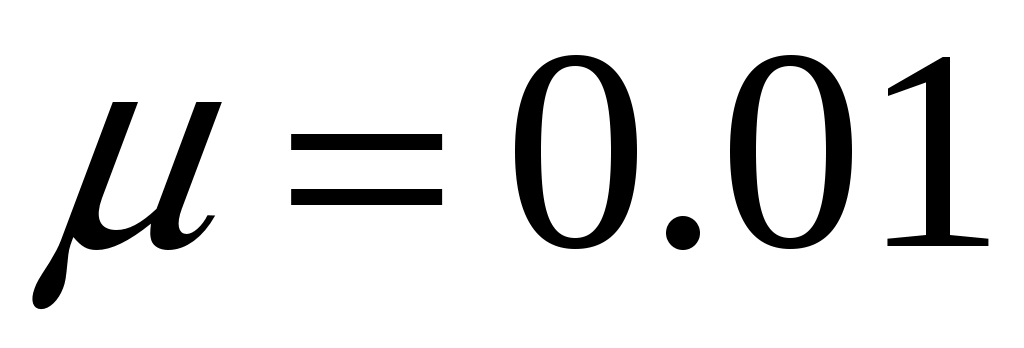 ,
, 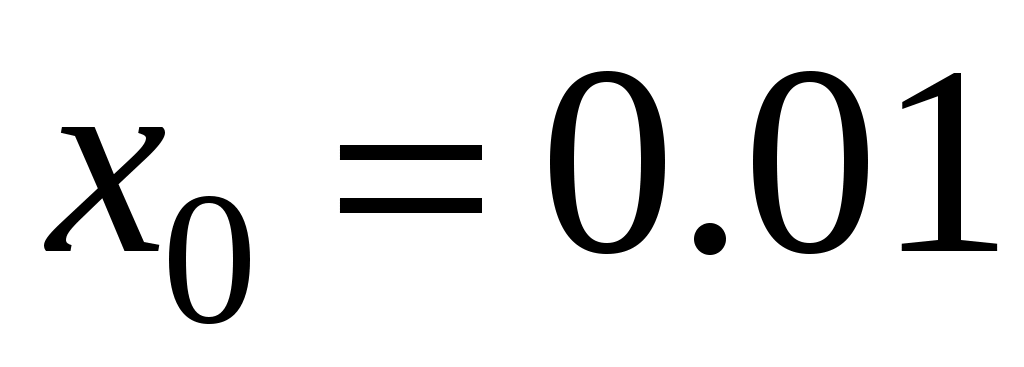 м.
м.
Математическая модель
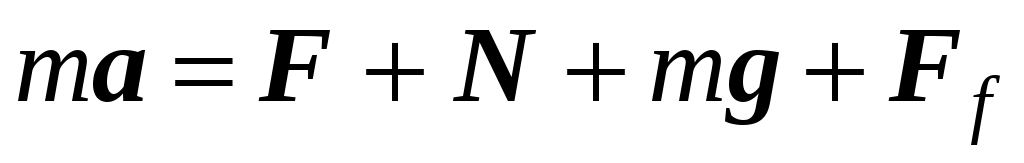 (19.1)
(19.1)
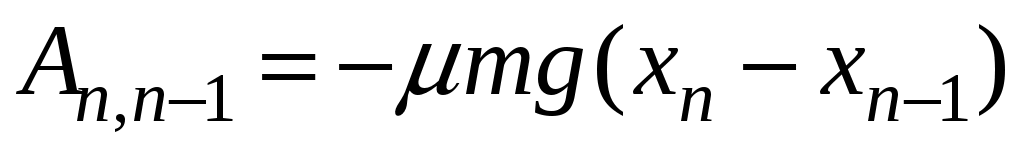 (19.2)
(19.2)
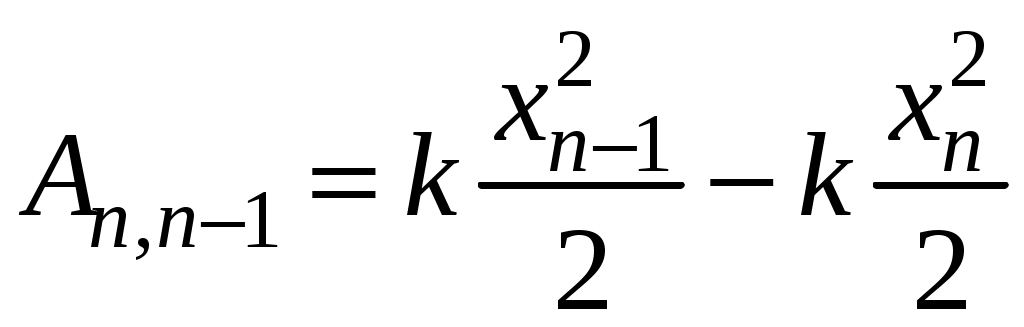 (19.3)
(19.3)
Знак минус в (19.2) связан с тем, что сила трения направлена против смещения бруска,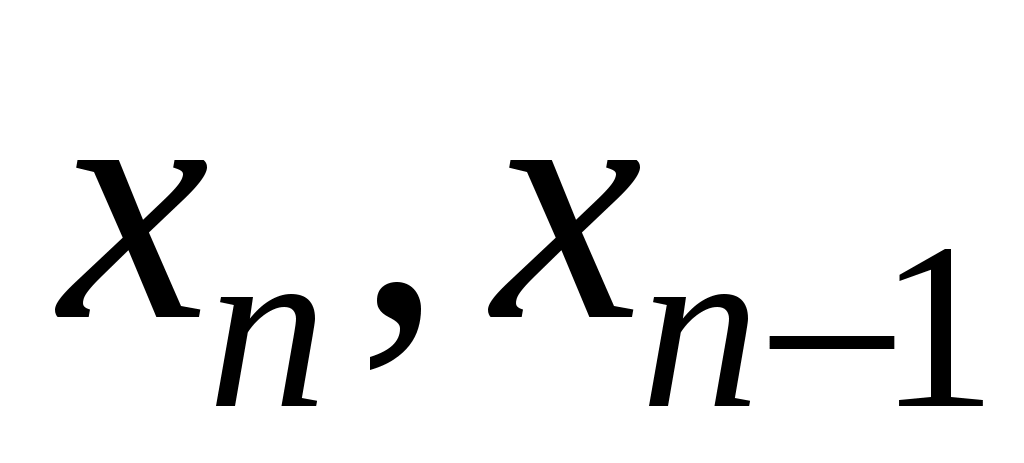 координаты точек остановки на полупериоде.
координаты точек остановки на полупериоде.
Решение
Процесс движения бруска показан на рис.1
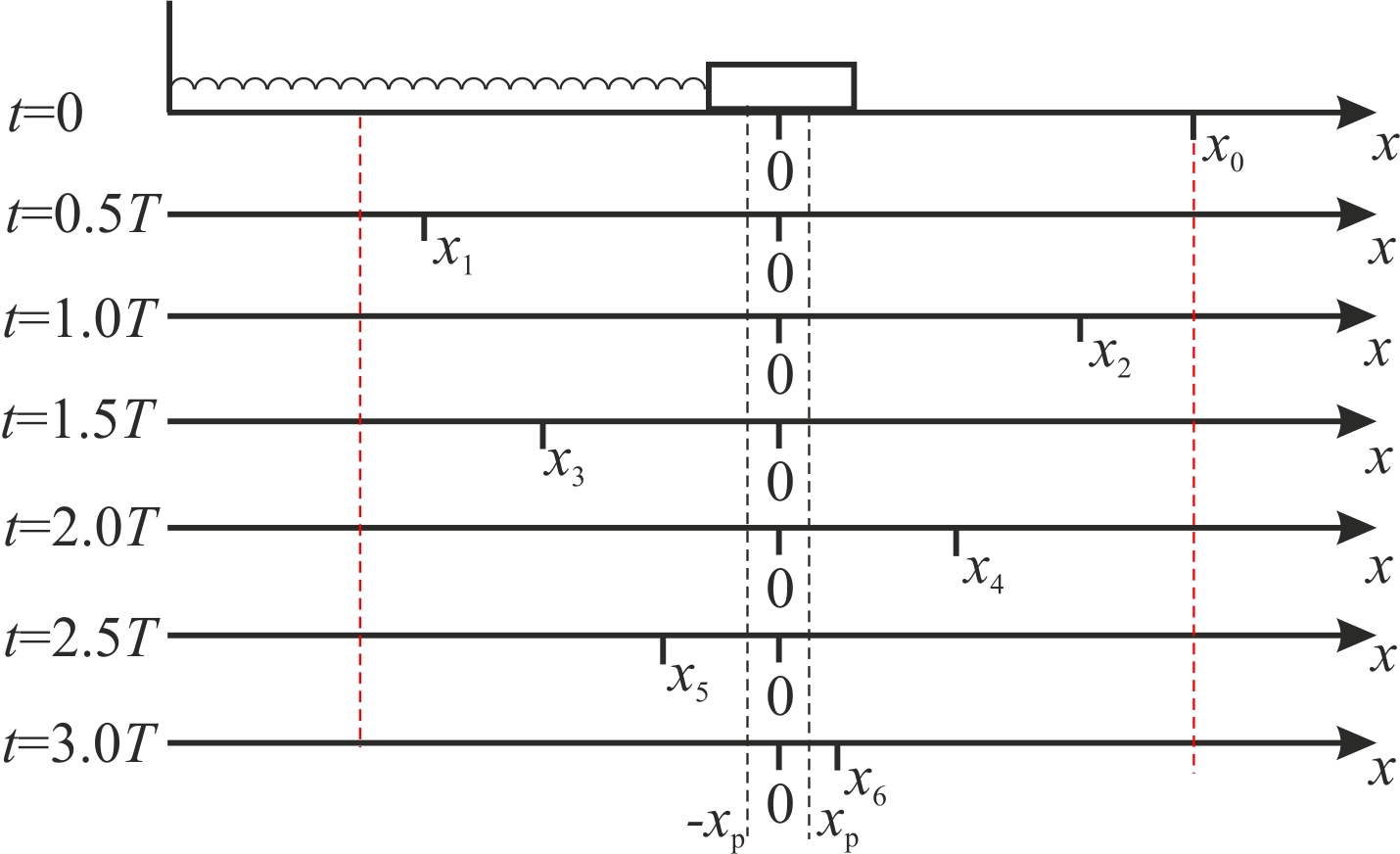
Рис.19.1. Координатно-временная развертка крайних положений бруска
Решение
Из (19.2) и (19.3) следует
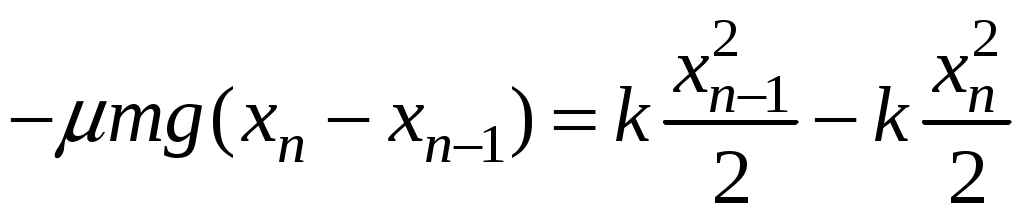 (19.4)
(19.4)
Определим область застоя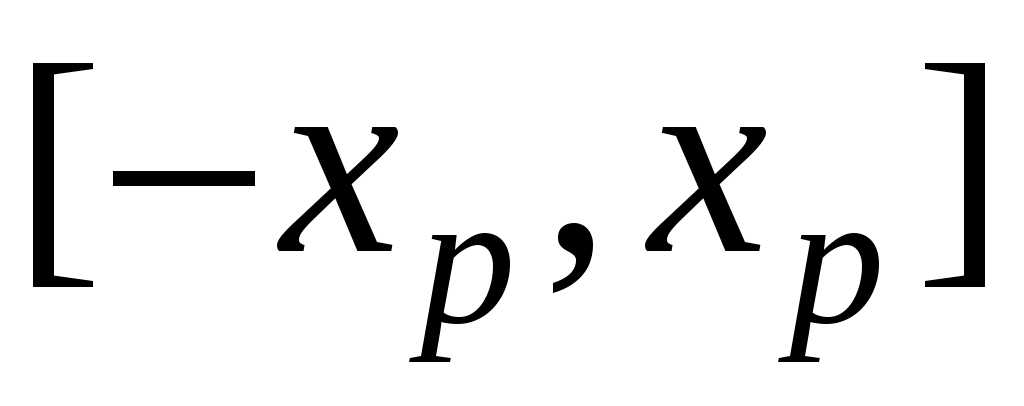 , в которой сила упругости в точности компенсируется силой трения покоя
, в которой сила упругости в точности компенсируется силой трения покоя
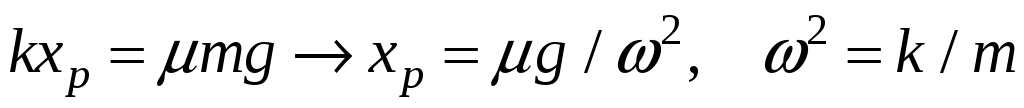
, (19.5)
Из (19.4) координаты крайних точек остановки равны
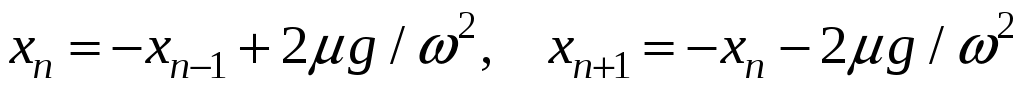 . (19..6)
. (19..6)
Колебания продолжаются до тех пор, пока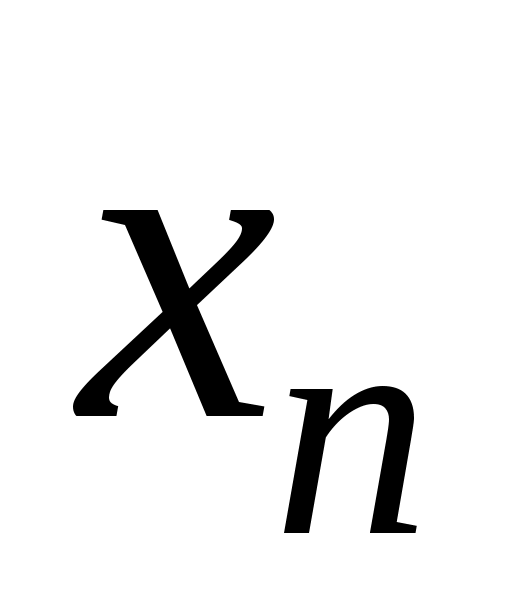 не попадет в область застоя, а именно для данных численных параметров получаем:
не попадет в область застоя, а именно для данных численных параметров получаем:
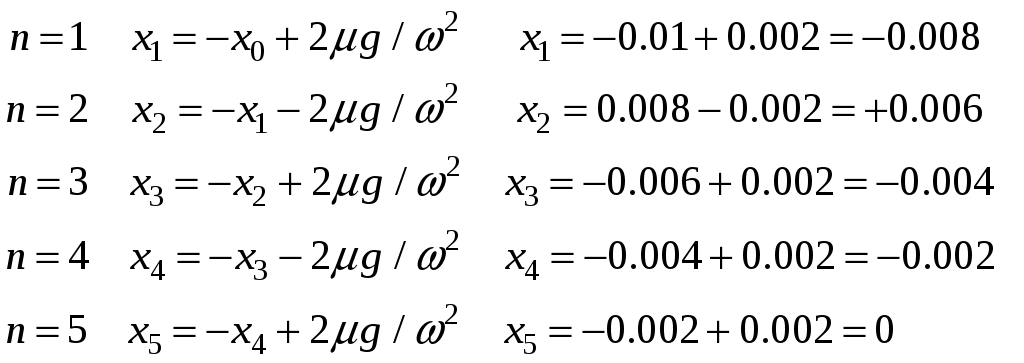
Время движения равно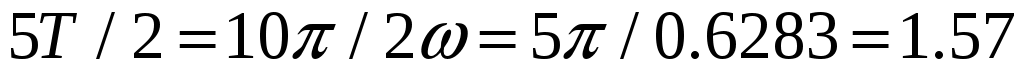 с.
с.
Для проверки проделаем численный расчет движения бруска на основе модели (19.1), проектируем на горизонтальную ось, получаем уравнение движения
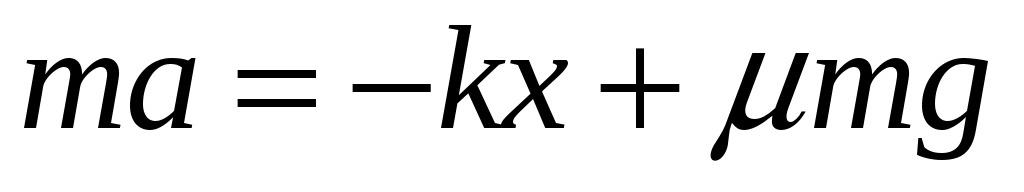 (19.7)
(19.7)
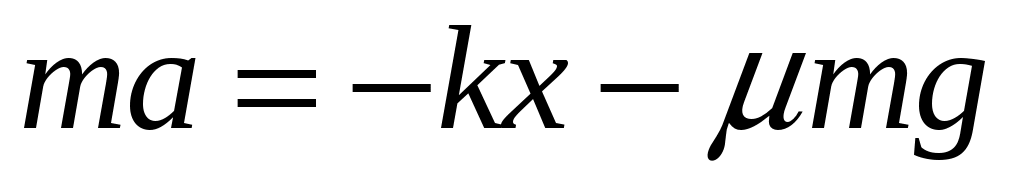 (19.8)
(19.8)
На рис.19.2 представлен результат численного расчета данной модели (текст программы приведен в Приложении)
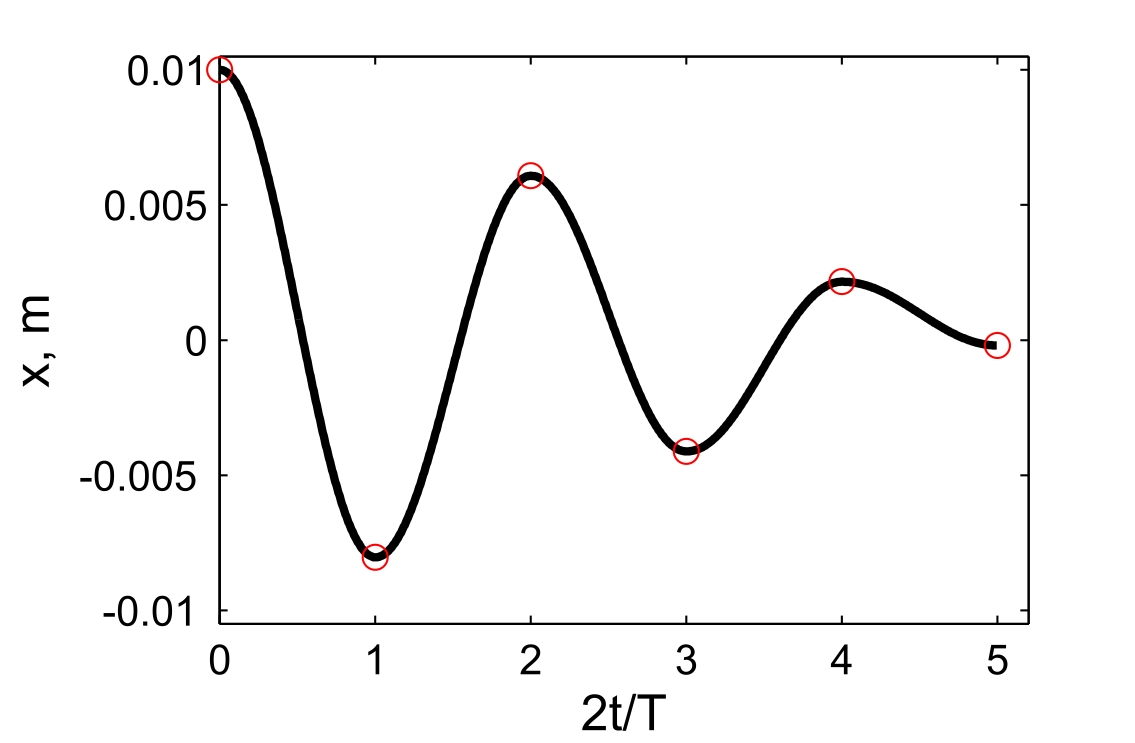
Рис. 19.2. График колебаний бруска, рассчитанный по модели (19.7), (19.8). Кружки отмечают крайние положения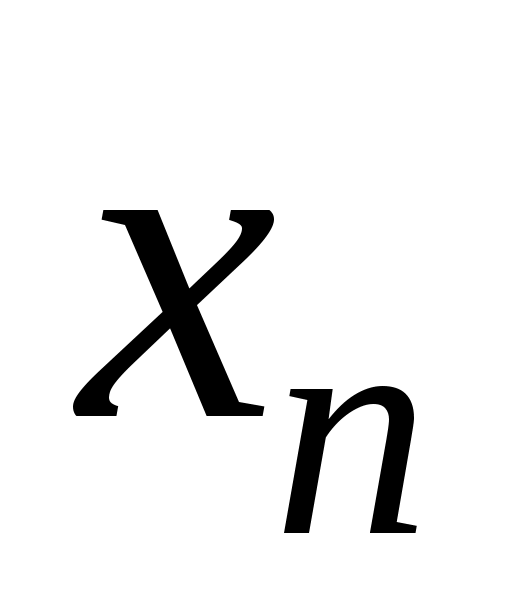 бруска, рассчитанные по формуле (19.6)
бруска, рассчитанные по формуле (19.6)
Несмотря на совпадения крайних положений бруска с положениями бруска, рассчитанными по модели (7.7) и (7.8), мы получили правдоподобный результат, поскольку в решении мы не учли область застоя около положения равновесия. График скорректированного решения приведен на рис.19.3.
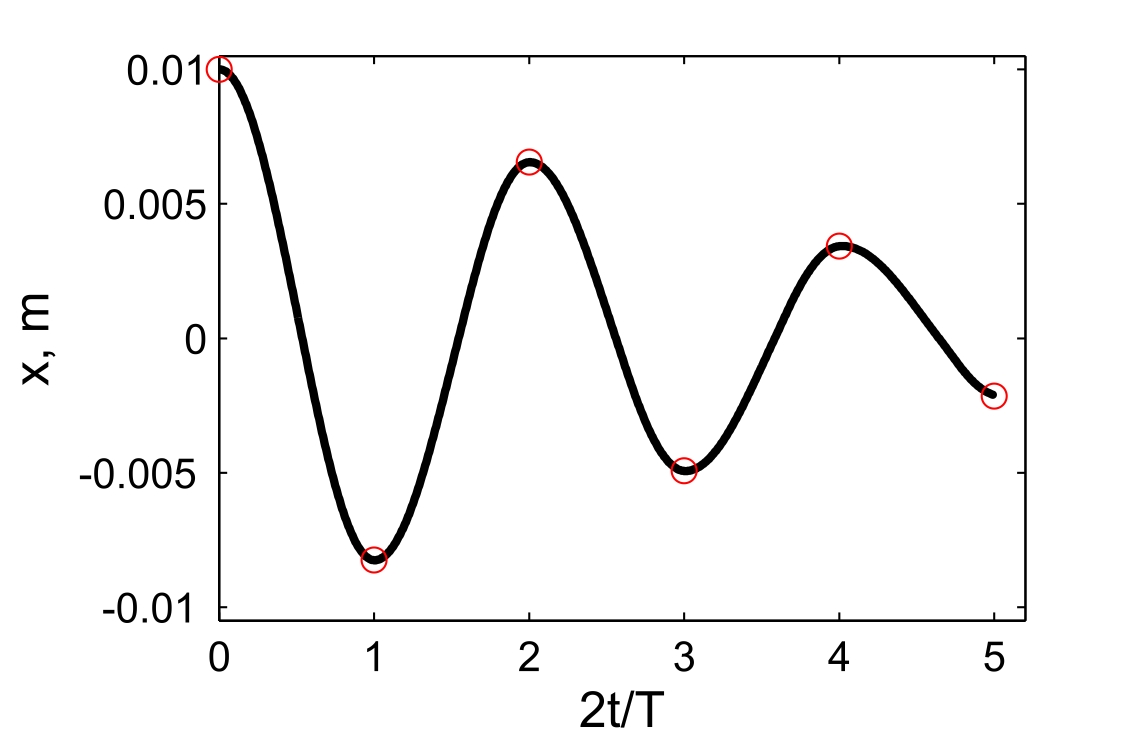
Рис. 19.3. График колебаний бруска, рассчитанный по модели (19.7), (19.8) с учетом области застоя. Кружки отмечают скорректированные крайние положения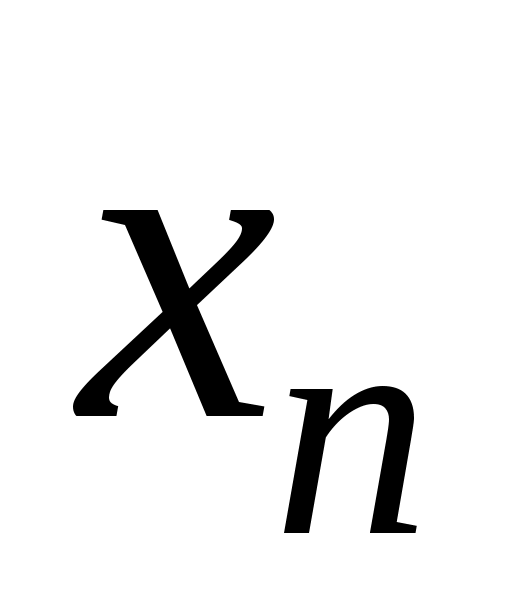 бруска.
бруска.
Таким образом, колебания бруска затухают слабее, поскольку в области застоя брусок движется равномерно. Получается парадокс, шероховатость горизонтальной плоскости везде одинакова, а в области застоя работу силы трения не учитываем.
Ответ: Маятник совершил 2.25 колебания в течение 1.57 секунд.
19.1. Груз массой 0.5 кг подвешен к пружине, жесткость которой 32 Н/м, и совершает затухающие колебания. Определите период затухающих колебаний, если за время двух колебаний амплитуда уменьшилась в 3 раза. Построить график зависимости
18.4. Материальная точка совершает колебания по закону синуса с амплитудой 10 см, частотой 2 Гц и начальной фазой 30 градусов. Полная энергия колеблющейся точки 0.077 Дж. Через какой промежуток времени от начала движения кинетическая энергия станет равной потенциальной? Построить график зависимости
18.5. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями
18.6. Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0 с частотой 4.00 с-1. В некоторый момент времени координата частицы равна 25 см и ее скорость 100 см/с. Найти координату и скорость частицы через 2.4 с после этого момента времени. Построить график зависимости
18.7. Определите амплитуду гармонических колебаний материальной точки, если полная энергия колеблющейся точки 0.04 Дж, а максимальная сила, действующая на точку, равна 2 Н. Привести поясняющий рисунок и указать основные параметры
18.8. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты
18.9. На доске лежит груз массой 10 кг. Доска совершает гармонические колебания по закону косинуса в вертикальном направлении с периодом 0.5 с и амплитудой 2 см. Определите величину давления
18.10. Найти период малых поперечных колебаний шарика массы 40 г, укрепленного на середине натянутой струны длины 1 м. Силу натяжения струны считать постоянной и равной 10 Н. Массой струны и силами тяжести пренебречь. Построить график зависимости
18.11. Уравнение изменения силы тока в колебательном контуре дано в виде
18.12. Колебательный контур имеет индуктивность 0.23 Гн, емкость конденсатора 7 мкФ. Сопротивление контура 40 Ом. Конденсатор заряжен 0.56 мКл. Найдите: а) период колебаний, б) логарифмический декремент затухания колебаний λ. Напишите уравнение зависимости разности потенциалов на обкладках конденсатора от времени. Построить векторную диаграмму напряжений и привести графики
18.13. Заряженный конденсатор емкостью 0.35 мкФ подключили к катушке индуктивностью 0.25 мГн. Через какое время после подключения катушки энергия электрического поля станет равной энергии магнитного поля катушки? Построить графики энергий. Активным сопротивлением контура пренебречь.
18.14. В колебательном контуре, состоящем из конденсатора и катушки индуктивностью 2.5 мГн, происходят электромагнитные колебания, при которых максимальная сила тока 10 мА. Определить емкость конденсатора, если максимальная разность потенциалов на его обкладках достигает 50 В, а активным сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики
18.15. Определить частоту собственных колебаний колебательного контура, который состоит из конденсатора емкостью 2 мкФ и катушки длиной 10 см и радиусом 1 см, содержащим 500 витков. Учесть, что происходят электромагнитные колебания, при которых максимальная сила тока в контуре 10 мА. Сопротивлением катушки можно пренебречь. Построить векторную диаграмму напряжений и привести графики
18.16. Колебательный контур имеет индуктивность 1.6 мГн, емкость конденсатора 0.04 мкФ и максимальную разность потенциалов на обкладках конденсатора 200 В. Чему равна максимальная сила тока в контуре? Активное сопротивление контура мало. Построить векторную диаграмму напряжений и привести графики
19.Затухающие колебания
Пример 19.1. Горизонтальное колебательное движение бруска при наличии сухого трения.
Пружинный маятник представляет собой брусок массой
Для численных расчетов принять
Математическая модель
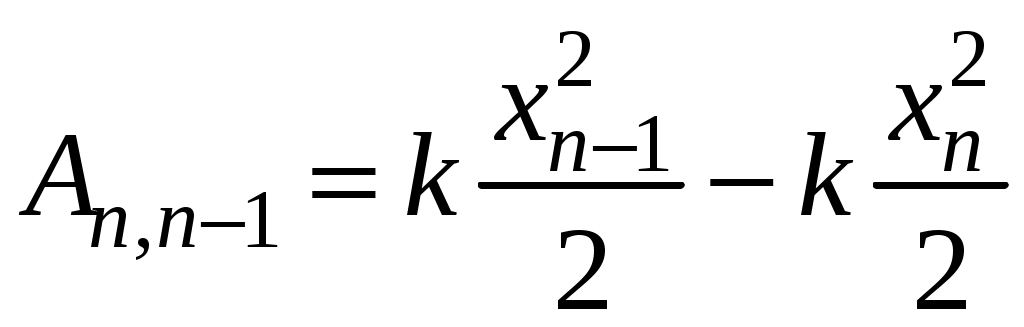 (19.3)
(19.3)Знак минус в (19.2) связан с тем, что сила трения направлена против смещения бруска,
Решение
Процесс движения бруска показан на рис.1

Рис.19.1. Координатно-временная развертка крайних положений бруска
Решение
Из (19.2) и (19.3) следует
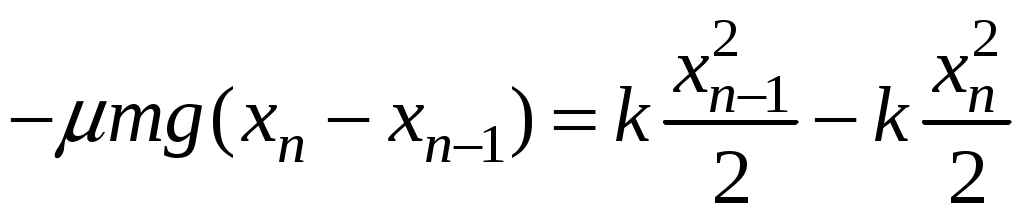 (19.4)
(19.4)Определим область застоя
, (19.5)
Из (19.4) координаты крайних точек остановки равны
Колебания продолжаются до тех пор, пока
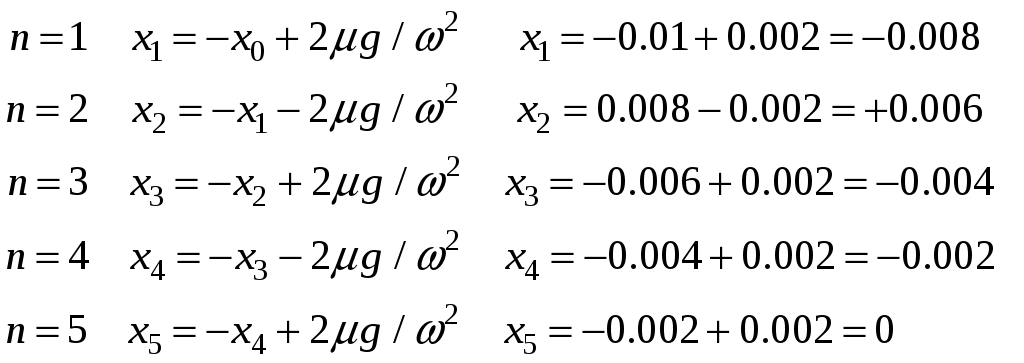
Время движения равно
Для проверки проделаем численный расчет движения бруска на основе модели (19.1), проектируем на горизонтальную ось, получаем уравнение движения
-
Движение справа — налево
-
Движение слева — налево
На рис.19.2 представлен результат численного расчета данной модели (текст программы приведен в Приложении)

Рис. 19.2. График колебаний бруска, рассчитанный по модели (19.7), (19.8). Кружки отмечают крайние положения
Несмотря на совпадения крайних положений бруска с положениями бруска, рассчитанными по модели (7.7) и (7.8), мы получили правдоподобный результат, поскольку в решении мы не учли область застоя около положения равновесия. График скорректированного решения приведен на рис.19.3.

Рис. 19.3. График колебаний бруска, рассчитанный по модели (19.7), (19.8) с учетом области застоя. Кружки отмечают скорректированные крайние положения
Таким образом, колебания бруска затухают слабее, поскольку в области застоя брусок движется равномерно. Получается парадокс, шероховатость горизонтальной плоскости везде одинакова, а в области застоя работу силы трения не учитываем.
Ответ: Маятник совершил 2.25 колебания в течение 1.57 секунд.
19.1. Груз массой 0.5 кг подвешен к пружине, жесткость которой 32 Н/м, и совершает затухающие колебания. Определите период затухающих колебаний, если за время двух колебаний амплитуда уменьшилась в 3 раза. Построить график зависимости