Сызықты емес жүйелердің зерттеуді жуықталған әдістер арқылы жүйенің барлық динамикалық қасиеттері жайында қажетті толық мәліметтер ала алмаймыз, бірақ Олардың көмегімен арнайы қажетті сұрақтарға жауап берілуі мүмкін, мысалы, орнықтылығы, автотербелістің бар болуы, кез келген жеке режимдер сипаттамалары және тағы басқа.
Айталық n-дәрежелі жүйені сипаттайтын теңдеулер бірінші дәрежедегі теңдеулер жиынтығы түрінде көрсетілсін:

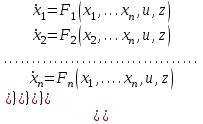(2.1)

мұндағы 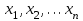жүйе жағдайын анықтайтын тәуелсіз айнымалылар, u және z басқарушы және қоздырушы әсерлер.

Жүйенің әрбір жағдайларына 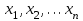айнымалыларының анықталған және нақты мәндері сәйкес келеді. Бұл айнымалыларды кейбір М нүктесінің тікбұрышты координаталары түрінде көрсетуге болады, Оларды кескіндейтін нүкте деп атаймыз. Егер уақыт аралығында 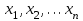тәуелсіз координаталардың өзгерісі болса, онда НӘфазалық траектория деп аталатын қисықты түзе отырып, кескінделетін нүкте берілген бір координаталық жүйеде орын ауыстырады

12. 
    Бейсызықты автоматты басқару жүйесінің фазалық траекториялары
    

Автономды дифференциалдық теңдеулер жүйесін қарастырайық:

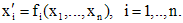12. 
                                                                            (1)
    

(1) үшін айнымалылар кеңістігі   фазалық кеңістік болып табылады. Егер n=2, онда фазалық кеңістік фазалық жазықтық болып табылады. Мұндағы t нүктесі    - фазалық нүкте деп аталады. Ал    қисық сызықтар фазалық траекториялар. Фазалық траекторияның бағыты деп t артатын бағыттағы фазалық нүктенің қозғалыс бағытын    айтады. Ал фазалық жазықтықта фазалық траекториялар салатын сурет фазалық портрет деп аталады.

(1) жүйеде, 

---

 оң жақтары үздіксіз және үздіксіз жеке туындылар болса    , онда фазалық траекторияның үш түрі мүмкін: нүкте, тұйықталған, тұйықталмаған қисық. Нүктелер жүйенің тепе-теңдік күйіне сәйкес келеді. Тұйықталған қисық периодты шешімді, ал тұйықталмаған – периодты емес шешімді білдіреді.

n=2 кезінде (1) жүйесі тұрақты коэффициенттері бар біртекті дифференциалдық теңдеулер жүйесі болсын:

                                                                                        (2)

(2) жүйені сапалы зерттеудің негізгі мақсаты – оның фазалық кеңістігінің сапалы суретін алу. Жүйенің фазалық траекториясының жүрісі сипаттамалық теңдеудің түбірлерін   және   анықтайды:

12. 
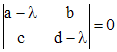                                     .                                                                    (3)
    

Бұл түбірлер нақты немесе кешенді шамалар бола алады.

14. 
    Фазалық жазықтық тәсілі бойынша бейсызықты жүйелердегі үрдістерді зерттеу
    

Фазалық жазықтық-бұл өтпелі процесті сипаттайтын кез-келген айнымалылар орналасқан координаталық осьтер бойымен жазықтық. Ең жиі қолданылатындар: келесі координат x - Шығыс координаты, y=dx/dt – Шығыс координатасының өзгеру жылдамдығы. Содан кейін екінші ретті дифференциалдық теңдеу бірінші ретті екі теңдеуге дейін азаяды.

Фазалық жазықтықтың теңдеуіне өту үшін уақытты теңдеуден алып тастау керек. Ол үшін екінші теңдеуді біріншіге бөліңіз.

Теңдеудің шешімі-y= F(x) функциясы, оның фазалық жазықтықтағы графикалық бейнесі фазалық траектория деп аталады.

Фазалық жазықтық әдісімен зерттеу тәртібі

1. Тепе-теңдіктің барлық мүмкін күйлерін анықтаймыз (dx / dt = 0;

dy/dt=0)

2. Тепе-теңдік күйінің табылған мәндері алғашқы жуықтау теңдеуі бойынша шағын аудандардағы тұрақтылыққа зерттеледі.

3. Фазалық портрет кез-келген бастапқы жағдайда салынады және жабық траекториялардың (шекті циклдердің) болуы анықталады.

4. Егер зерттелетін жүйеде шекті циклдер болса, онда олардың тұрақтылығы зерттеледі.

14. 
    Фазалық траекториялар әдісі
    

---

Сызықтық емес жүйелерді зерттеу үшін автоматты басқару теориясында жеке әдістер жасалынған және қолданылады, олардың әрқайсысы белгілі бір мүмкіндіктерге ие және зерттеу міндеттерінің шектеулі саласында тиімді. Фазалық траектория әдісі және амплитудалық жиілік әдісі (гармоникалық сызықтық әдіс) ең көп қолданылады. Екеуі де бұл әдісті қаралатын болады бұдан әрі.

Фазалық траекториялар әдісі зерттелетін сызықтық емес жүйенің әрекеті уақыт аймағында емес (жүйеде процестердің теңдеулері түрінде), бірақ жүйенің фазалық кеңістігінде (фазалық траекториялар түрінде) қарастырылады және сипатталады.

Сызықтық емес автоматты басқару жүйесінің күйі жүйенің фазалық координаттарын қолданумен сипатталады




жүйенің фазалық кеңістігіндегі жүйе күйінің векторын анықтау

Y (y1, y2, y3,...yn).

Фазалық координаттарды қарастыруға енгізу кезінде сызықты емес жүйеде еркін процесс үшін n ретті сызықты емес дифференциалдық теңдеу


бірінші ретті N дифференциалдық теңдеулер жүйесіне түрлендіріледі

14.   1   2   3   4   5   6

---

Фазалық кескіннің ерекше нүктелері мен сызықтары

Егер басқару жүйесінің теңдеулері қалыпты түрде ұсынылса, онда жүйенің күй векторы оның күйін нақты анықтайды. Нүкте күй кеңістігіндегі жүйенің әр күйіне сәйкес келеді. Жүйенің ағымдағы күйіне сәйкес келетін нүкте кескін нүктесі деп аталады. Күй өзгерген кезде кескін нүктесі траекторияны сипаттайды. Бұл траектория фазалық траектория деп аталады. Бастапқы шарттардың барлық түрлеріне сәйкес келетін фазалық траекториялардың жиынтығы фазалық портрет деп аталады.

Екі өлшемді фазалық кеңістік жағдайында фазалық траектория мен фазалық портретті көрнекі түрде көрсетуге болады. Екі өлшемді фазалық кеңістік фазалық жазықтық деп аталады.

Фазалық жазықтық-Координаталық жазықтық, онда екінші ретті жүйенің күйін анықтайтын екі айнымалы (фазалық координаттар) координаталық осьтер бойымен орналасады. Фазалық портреттің құрылысына негізделген басқару жүйесін талдау және синтездеу әдісі фазалық жазықтық әдісі деп аталады.

14. 
    Фазалық траектория теңдеуі бойынша фазалық кескіннің салынуы
    

х-y фазалық жазықтықта фазалық траектория сызғанда оны салудың келесі жалпы ережелерін назарға алған дұрыс.

1. 
   Фазалық жазықтықта y=0 мәнінде, өзгеру жылдамдығы нөлге тең.
   
2. 
   y –тің оң кезінде, яғни фазалық жазықтықтың жоғарғы жағында бейнелеуші нүкте сНӘдан оңға қарай жылжиды, ал y -тің теріс мәнінде, яғни фазалық жылдамдықтың төмен жағында керісінше оңнан сНӘға қарай жылжиды.
   
3. 
   фазалық траекториялар өзара бір-бірімен қиылыспайды. Тек айрықша өрнектерде қиылысуы мүмкін.
   

Фазалық траекториялар y=f(x) фазалық теңдеуі бойынша салынады, оны табудың алдында ең алдымен жүйенің бастапқы дифференциалды теңдеулерінен фазалық траекториясының дифференциалды теңдеуін аламыз.



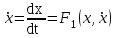
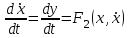(2.2)

Бірінші теңдеуді екінші теңдеуге бөле отырып уақыттан арыламыз

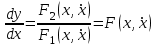(2.3)

Кейбір жағдайларда бұл теңдеу интегралданып, фазалық траекторияның теңдеуі 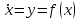болып табылады, алынған теңдеу бойынша жүйенің фазалық портреті тұрғызылады.

---

Қисық-сызықты сипаттамалары бар буындардан тұратын жүйелер үшін, фазалық жазықтықта (2.3) теңдеуінің сондай немесе басқа түрі кездесетін аймақтар белгіленуі мүмкін.

14. 
    Фазалық траекторияны изоклин әдісі бойынша жуықтап салудың әдісі
    

Фазалық портретті салу үшін изоклин әдісі қолданылады-интегралдық қисықтарды белгілі бір бұрышпен кесіп өтетін сызықтар фазалық жазықтықта қолданылады. Изоклин теңдеуін оңай алуға болады. Қойыңыз

мұндағы А-белгілі бір тұрақты мән. А мәні тангенстің фазалық траекторияға көлбеу бұрышының тангенсін білдіреді және ол – ¥ - дан +¥ - ға дейінгі мәндерді қабылдай алады. Dy/dx орнына а мәнін ауыстыру арқылы изоклин теңдеуін аламыз:

.   
теңдеу жазықтықтың әр нүктесінде P (x, y) = 0,Q (x, y) = 0 болатын нүктені қоспағанда,тиісті интегралдық қисыққа жалғыз тангенсті анықтайды, онда тангенс бағыты белгісіз болады, өйткені ол белгісіз болады.:
.
Изоклин әдісінің мәні дифференциалдық теңдеуде фазалық траекторияны, дифференциалды тұрақтыға ауыстыру болып табылады . Содан кейін y=f(x,m) түрінің қарапайым теңдеуі алынады.

Фазалық траекторияның құрылысы изоклиннен басталады y=f(x,m) әр түрлі мәндермен m. бұл жағдайда m берілген изоклинді кесіп өтетін фазалық траекторияға тангенстің бұрыштық коэффициентін білдіреді. Изоклин көмегімен құрылыстың мысалы 9.7-суретте келтірілген.

Егер сызықты емес элемент күрделі сипаттамаға ие болса, онда алдымен сызықты емес сипаттаманы жеке сызықтық бөліктерге бөлу үшін сызықты емес жуықтауды қолдану керек. Әр бөлім үшін теңдеулерді шығару керек изоклин y=f (x, m). Осылайша салынған фазалық траекторияларды бастапқы диапазондарға сәйкес бір жазықтықта біріктіру керек.

14. 
    Автотербеліс
    

Автотербеліс (Автоколебание) - сырттан энергия алмастан жүйенің ішіндегі энергия шығыны осы жүйедегі активті элемент есебінен толықтырылғанда жүйеде пайда болатын АВТ өшпейтін тербеліс.

Автотербелістің жиілігі және амплитудасы жүйенің өзіне тән қасиеттері бойынша анықталады. Шамды және транзисторлық генераторлардағы тербелістер осы автотербелістерге жатады.^[1] Бұдан бұрын айтып кеткеніміздей, нақты тербелмелі жүйедегі тербеліс энергиясы біртіндеп жылу энергиясына айналады да, еркін тербелістер өшеді. Тербеліс өшпеу үшін энергия шығынын толықтырып отыру керек. Мұның екі жолы бар.

---

Смотрите также файлы

• Контрольнооценочные средства.pdf

• Азиатское происхождение скифов по Геродоту.pptx

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx

• Урок 18 Раздел Мультимедиа (сквозная тема В здоровом теле здоровый дух!) Ф. И. О. учителя Дата.doc

• Контрольная работа на промежуточной итоговой аттестации (12 класс). Фамилия, имя дата.docx