Ляпуновтың сипатталған теоремалары қандай да бір мағынада қолдануға мүмкіндік береді. Шамамен айтқанда, бұл Теоремалардың шарттары қажет: егер тепе-теңдік позициясы белгілі бір тұрақтылық қасиеттеріне ие болса, онда жүйеде тиісті талаптарға жауап беретін Ляпунов функциясы бар. Қарапайым мысал ретінде, егер сызықтық автономды жүйе болса

x′ = Ax

асимптотикалық тұрақты, онда RN\{0} оң Ляпунов функциясы бар, ол қанағаттандырады (5). Шынында да, асимптотикалық тұрақтылық А матрицасының барлық меншікті мәндерінің теріс нақты бөліктерге ие болуын қамтамасыз етеді, сондықтан жүйе экспоненциалды түрде тұрақты болады. Φ(t) — бұл жүйенің нөлдегі қалыпты іргелі матрицасы (Φ(t) = eAt). Экспоненциалды тұрақтылық оң M және α болуын қамтамасыз етеді

/ / Φ (t) / / ≤ me-αt T ≥ 0 кезінде.

Қойыңыз V(x) = ∫ ∞ 0 ||Φ(s)x||2ds.

26. Бейсызықты басқарылатын жүйелердің орнықтылығы

Егер жүйенің кем дегенде бір элементі бейсызықты болса, жүйе бейсызықты деп аталады. Мұндай жүйенің жұмысы бейсызықты дифференциалдық теңдеулермен сипатталады. Бейсызықты жүйенің сызықты жүйеден айырмашылығы – сызықты жүйелер бастапқы күйінен ауытқығанда орнықты болса, үлкен ауытқу кезінде де орнықты болады, ал бейсызықты жүйе аз ауытқуда орнықты болғанымен, үлкен ауытқуда орнықсыз болады. Бейсызықты жүйелердің ерекшелігі – оларда суперпозиция принципі қолданылмайды.

Жүйелердің динамикалық сипаттамаларын зерттеу кезінде оның буындары сызықты деп алынады, себебі бұл жағдайда сызықты теңдеулерді ғана талдау керек, ал суперпозиция принципі математикалық жағынан тиімді түрде сигналдарды құраушыларға жіктеуге мүмкіндік береді, соның нәтиіжесінде қойылған есепті оңай шешуге болады.

Буын бейсызықты деп аталады, егер оның шығыс сигналының кіріс сигналына тәуелділігі сызықты теңдеумен (мысалы, дифференциалдық теңдеумен) сипаттала алса.

27.Орнықтылықтың В.М.Попов критерийі

Сызықтық емес басқару және тұрақтылық теориясында Попов критерийі-Василий М. Поповтың сызықтық емес жүйелер класының абсолютті тұрақтылығы үшін тұрақтылық критерийі, оның сызықтық емес сипаты ашық сектордың жағдайын қанағаттандыруы керек. Шеңбер критерийі уақыт бойынша сызықтық емес өзгеретін жүйелерге қолданылуы мүмкін, ал Попов критерийі тек автономды (яғни уақыт бойынша инвариантты) жүйелерге қолданылады.

---

Лурье жүйелерінің Поп-класын зерттеген: мұндағы x R r n, ω, u, y-скалярлар,ал A, b, c және d өлшемдері сәйкес келеді. Сызықтық емес элемент Φ: r → r-ашық секторға жататын уақыт өзгермейтін сызықтық емес (0,∞), яғни Φ(0) = 0 және Y Φ(y)> 0-ге тең емес барлық y үшін 0. Попов зерттеген жүйенің басында тірек бар екенін және кіреберістен шығысқа тікелей өту жоқ екенін ескеріңіз, ал u-ден y-ге дейінгі беріліс функциясы берілген

28.Асимптотикалық және асимптотикалық емес орнықтылықтың анықтамасы

асимптотикалық теория, немесе үлкен үлгі теориясы, қасиеттерін бағалауға арналған негіз болып табылады бағалаушылар және статистикалық тесттер. Осы шеңберде, деп жиі болжанады үлгі мөлшері n шексіз өсуі мүмкін; бағалаушылар мен сынақтардың қасиеттері содан кейін шегі бойынша бағаланады n → ∞. Іс жүзінде шекті бағалау іріктелген үлкен өлшемдер үшін де жарамды деп саналады. Статистикалық мәселелердің көпшілігі мәліметтер жиынтығынан басталады өлшемі n. Асимптотикалық теория қосымша деректерді жинауға болады (негізінен), осылайша іріктеме мөлшері шексіз өседі деп болжайды, яғни. n → ∞. Болжам бойынша, шектеулі мөлшердегі үлгілер үшін қол жетімді емес көптеген нәтижелер алуға болады. Мысал ретінде үлкен сандардың әлсіз заңы. Заңда реттілік үшін деп көрсетілген тәуелсіз және бірдей бөлінген (IID) кездейсоқ шамалар X₁, X₂, …, егер әрбір кездейсоқ шамадан бір мән алынады және біріншісінің орташа мәні n мәндер ретінде есептеледі X_n, содан кейін X_n ықтималдылыққа жақындау халыққа дегенді білдіреді E [X_мен] сияқты n → ∞.^[2]

Асимптотикалық теорияда стандартты тәсіл болып табылады n → ∞. Кейбіреулер үшін статистикалық модельдер, асимптотиканың сәл өзгеше тәсілдерін қолдануға болады. Мысалы, панельдік деректер, деректердегі бір өлшем тұрақты болып қалады, ал екінші өлшем өседі деп болжанады: Т = тұрақты және N → ∞, немесе керісінше.

30. Бейсызықты жүйенің орнықтылығын екінші (тура) Ляпунов әдісі бойынша зерттеу

Орнықтылықты зерттеудiң жалпы әдiсi АРЖ-ның   жоспарлау (басқарушы) және   қоздыру әсерлерi тудыратын   , реттелетiн шаманың өзгеруi үшiн жазылған

 (1)

дифференциал теңдеуiн талдаумен тұжырымдалады.   ,   мәндерiн және олардың туындыларын нөлге тең деп алсақ, сипаттама теңдеуi

---

 (2)

болатын бiртектес

 (3)

дифференциал теңдеуiн аламыз.

АРЖ-ның орнықты екендiгін (3) теңдеуiн шешу арқылы анықтауға болады. Оның шешiмi өтпелi процестi сипаттайды 

Мұндағы   — интегралдау тұрақтысы, ол бастапқы шарттан анықталады;   — сипаттамалық теңдеудiң түбiрлерi.өтпелi процесс саны   түбiрлер санымен анықталатын құраушылар қосындысынан тұрады.

Жүйе орнықты болуы үшiн (4)-нiң шешiмi мына шартты қанағаттандыруы тиiс:

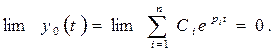 (5)

Бұл өрнек орнықтылық шартының аналитикалық өрнегi болады. Жалпы жағдайда   түбiрлерi комплекс болып келедi. Оған қоса олар түйiндес (сопряженный)   түбiрлердiң жұбын түзедi.

Орыс ғалымы, академик А. М. Ляпунов 1892 жылы бiрiншi болып орнықтылықтың дәл анықтамасын тұжырымдап, қозғалыстың орнықтылығын зерттеудiң жалпы әдiсiн жасады. А. М. Ляпунов былайша тұжырымдайды: Сызықты АРЖ орнықты болуы үшiн мынадай шарттар қажетті және жеткілiктi: сипаттамалық теңдеудiң барлық нақты түбiрлерiнiң терiс таңбалы, ал комплекс түбiрлерiнiң нақты бөлігi терiс таңбалы болуы тиiс.

---

31.Екінші (тура) Ляпунов әдісінің теоремалары

Ляпуновтың екінші әдісі (көп жағдайда оны тура әдіс деп те атайды), жалпы алғанда, өзі мен берілген теңдеуге сүйеніп алынған туындысы белгілі бір арнаулы шарттарды қанағаттандыратын функцияны табуға негізделген. Бұл әдісті пайдалану көп жағдайларда дифференциалдық теңдеуді шешпей-ақ оның шешімінің орнықты, орнықсыздығын анықтауға мүмкіндік береді.

Мына



облысында анықталған және



шарттарын қанағаттандыратын қанағаттандыратын   функциясын қарастырайық.

Мысалдар. Төмендегі жүйелердің нөлдік шешімдерінің орнықты, орнықсыздығын тексеру керек.

 үшін   функциясын алайық. Ол   облысында шектелген. Теңдеуге сүйеніп алынған туындысы мына түрде

яғни   Сондықтан



Теңдеудің нөлдік шешімі орнықсыз.

32. Екінші Ляпунов әдісінің геометриялық мағынасы

Ляпунов əдісі деп те аталатын Ляпуновтың тікелей əдісін қолданғанда бірінші тəртіп теңдеуі түріндегі автоматты жүйенің дифференциалды теңдеуін қолданамыз. n қатарындағы сызықтық емес жүй үшін бұл теңдеулер мына түрде болады:

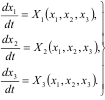 (1.1)

мұнда X1, X2,..., Xn функциялары туынды жəне сызықсыздықтың кез-келген түріне ие болады бірақ əрқашан

 шартын қанағаттандырады, себебі орныққан жағдайда барлық өтпелі ауытқулар мен туындылар тең болады. Ары қарай бізге келесі мағлұматтар керек болады.

Ляпунов функция әдісі дифференциалдық теңдеулер шешімдерінің тұрақтылығын зерттеуге жеткілікті күшті және икемді аппарат берді. Дифференциалдық теңдеулер шешімдерінің басқа қасиеттерін анықтау үшін қазір модификация қолданылады. Мысалы, жапон математигі Окамура ерітінділердің кеңеюін зерттеу үшін екінші Ляпунов әдісінің идеяларына ұқсас идеяларды қолданды, содан кейін Йошизава ерітінділердің шегі туралы ақпарат алу үшін осы әдісті қолданды.

---

Белгілі болғандай, Ляпунов теоремалары   туындысының белгісі бойынша тұрақтылықты бағалауға мүмкіндік береді, мұндағы   оң белгілі функция. Осылайша   теңсіздік зерттеледі. Орыс ғалымы С.А. Чаплыгин дифференциалдық теңсіздіктер теориясында дифференциалдық теңсіздіктерді кеңінен қолдана бастады. Теорияның дамуы Ляпунов функциясының әдісінің дифференциалдық теңсіздік әдісімен ұштасуына әкелді: олар Ляпунов функцияларын форманың дифференциалдық теңсіздіктерінде қарастыра бастады

бұл шешімдердің кеңістігі мен шектелуіне қатысты, атап айтқанда, қызықты қорытындылар алуға мүмкіндік береді.

33. В.М. Поповтың абсолютті орнықтылық критерийі

Бұл критерийді 1960 жылы румын ғалымы В.М.Попов ұсынды және ол бірмәнді статикалық бейсызықтылығы бар сызықсыз жүйенің абсолютті орнықтылығын зерттеуге мүмкіндік береді. Абсолютті орнықтылық деп 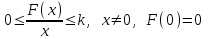шартын қанағаттандыратын кез-келген түрдегі бейсызықтылықтың толық орнықтылығы аталады.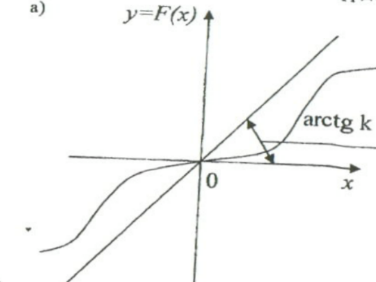



б)

4.1-сурет. Абсолютті орнықтылық сипаттамалары

Бұл сипаттамалар 0-к бұрышында жатады, немесе 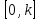класына жатады делінеді.

Егер жүйенің тепе-теңдігі абсолютті орнықты болса, онда НӘ барлық түзу сызықты сипаттамалар 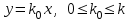үшін абсолютті орнықты, себебі бұл сызықтар берілген 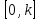класына жатады. Сызықты бөлігі орнықты және 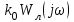сызықталған сипаттамасы бар ашық жүйенің векторының годографы

---

Смотрите также файлы

• Контрольнооценочные средства.pdf

• Азиатское происхождение скифов по Геродоту.pptx

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx

• Урок 18 Раздел Мультимедиа (сквозная тема В здоровом теле здоровый дух!) Ф. И. О. учителя Дата.doc

• Контрольная работа на промежуточной итоговой аттестации (12 класс). Фамилия, имя дата.docx